http://210.45.192.19/kecheng/jxcg/all/1_6/Fx/Fx4.htm
第一节关于分形与分维的概念013
210.45.192.19/kecheng/jxcg/all/1_6/Fx/Fx4.htm
轉為繁體網頁
轉為繁體網頁
例如,皮兰(Perrin)于1908年用显微镜测量了布朗运动的轨迹,虽然实际的布朗 ..... 由于布朗运动的随机性,每一步的位移矢量都是独立的,所以上式右边的第二项为 ...
布朗運動 送交者: 零加一中 2006年04月01日10:45:40 于 [靈機一動] 發送悄悄話 在二維平面,粒子做隨機運動,每單位時間內移動距離L,方向隨機.問時間N後,粒子離原點距離多少.位移X是個矢量,由N個長度為L的矢量相加而成.做點積得兩項.一項是每次位移的平方相加,NL^2.另一項是交叉項,許多COS相加.因為方向隨機,第二項平均後為零.所以位移的模是 SQRT(N)L . 這方法不限于二維.回到JTY的問題,如是單一方向,那算術平均即可.因交叉項不為零,也只能算術平均.但如不是一維,或一維方向隨機,他同事就是對的,用我的方法解.平均後就是 RMS.
- See more at: http://bbs.creaders.net/iq/bbsviewer.php?trd_id=160115&language=big5#sthash.5W48wlt8.dpuf
- See more at: http://bbs.creaders.net/iq/bbsviewer.php?trd_id=160115&language=big5#sthash.5W48wlt8.dpuf
布朗運動 送交者: 零加一中 2006年04月01日10:45:40 于 [靈機一動] 發送悄悄話 在二維平面,粒子做隨機運動,每單位時間內移動距離L,方向隨機.問時間N後,粒子離原點距離多少.位移X是個矢量,由N個長度為L的矢量相加而成.做點積得兩項.一項是每次位移的平方相加,NL^2.另一項是交叉項,許多COS相加.因為方向隨機,第二項平均後為零.所以位移的模是 SQRT(N)L . 這方法不限于二維.回到JTY的問題,如是單一方向,那算術平均即可.因交叉項不為零,也只能算術平均.但如不是一維,或一維方向隨機,他同事就是對的,用我的方法解.平均後就是 RMS.
- See more at: http://bbs.creaders.net/iq/bbsviewer.php?trd_id=160115&language=big5#sthash.5W48wlt8.dpuf

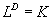 (
( ) (4-1-1)
) (4-1-1)
 (4-1-2)
(4-1-2)
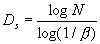 (4-1-4)
(4-1-4)

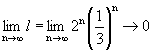

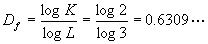 (4-1-5)
(4-1-5)
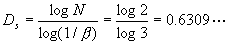
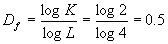

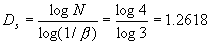 (4-1-6)
(4-1-6)
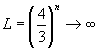 当
当

 (4-1-7)
(4-1-7)
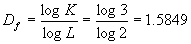 (4-1-8)
(4-1-8)
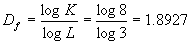 (4-1-9)
(4-1-9)
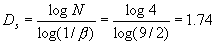

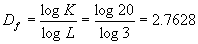 (4-1-10)
(4-1-10)
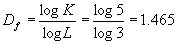
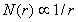

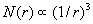 。
。
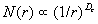 (4-2-1)
(4-2-1)
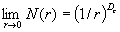 (4-2-2)
(4-2-2)
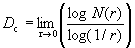 (4-2-3)
(4-2-3)
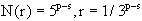



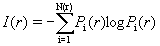 (4-2-4)
(4-2-4)
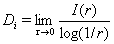 (4-2-5)
(4-2-5)

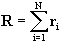
 . (4-2-6)
. (4-2-6)
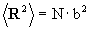 . (4-2-7)
. (4-2-7)
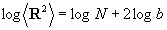 ,
,
 .
.
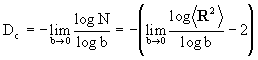 (4-2-8)
(4-2-8)
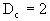
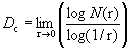
 (4-2-9)
(4-2-9)
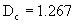

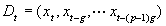




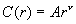 (4-3-1)
(4-3-1)
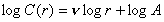 (4-3-2)
(4-3-2)
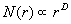


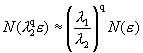 (4-5-1)
(4-5-1)



 (4-5-2)
(4-5-2)
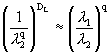

 (4-5-3)
(4-5-3)
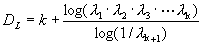 (4-5-4)
(4-5-4)

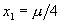
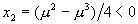 。
。
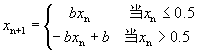 (4-5-5)
(4-5-5)
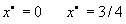
 (4-5-6)
(4-5-6)
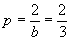
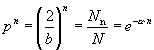 (4-5-7)
(4-5-7)
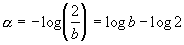 (4-5-8)
(4-5-8)
 (4-5-9)
(4-5-9)
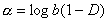
 (4-5-10)
(4-5-10)
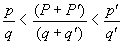 (4-5-11)
(4-5-11) (N→∞) (4-5-12)
(N→∞) (4-5-12)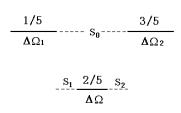
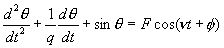


 ,
,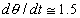 ;
; ,
,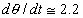 ;
; ,
, 。
。
 ,
, ;
;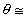 0,
0, ;
; ,
,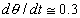 。
。


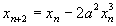 (4-5-13)
(4-5-13)
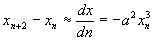 (4-5-14)
(4-5-14)
 (4-5-15)
(4-5-15)
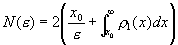 (4-5-16)
(4-5-16)
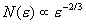
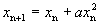
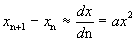
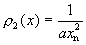 (4-5-17)
(4-5-17)
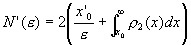 (4-5-18)
(4-5-18)

6.
 (4-5-19)
(4-5-19)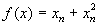 (4-5-20)
(4-5-20)


 (4-5-21)
(4-5-21)
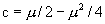
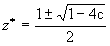 (4-5-22)
(4-5-22)
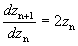 (4-5-23)
(4-5-23)




- See more at: http://bbs.creaders.net/iq/bbsviewer.php?trd_id=160115&language=big5#sthash.5W48wlt8.dpuf
第四章 分 形
引言
公元前300年,欧几里德在总结人们生产实践的基础上建立了几何学原理。于是几何学成了处理各种图形对象最常用的方法,对于其它对象如物理问题,当化解为图形时也常用到几何学原理。为了测量一条线段的长度,一个四边形的面积…;计算一块立方体木材的密度,一块带电圆球体的电势,…,人们通常不言明地假定:线段是笔直的,四边形是规则的,木材的密度是均匀的,而带电圆球体的表面是光滑的。在这些假设下就可以用一个整数去表征一个图形的维数,即大家熟悉的所谓三维空间、二维平面和一维线段等概念,在理论物理研究中甚至还会用到n维的假想空间,这里都利用了欧几里德几何学原理。伽利略曾经说过,自然界的语言是数学,其书写的符号是三角形、圆和其它图形。其实大自然是异常复杂、丰富多彩的,那些简单、正规的理想对象只是少数。例如,那块木材内部可能疏密不均,甚至存在空洞,如已被白蚁咬的千窗百孔;那个带电球体表面可能凹凸不平,如此等等。分形理论的创始人、美国科学家曼德布罗特(Mandelprot)曾说过:“浮云不呈球形,山峰不呈锥体,海岸线不是圆圈,树干不是光溜溜的,闪电永不会沿直线行进”,说的就是人们一般不应以简单的、理想的体系去对待实际体系。
另一方面应该注意到,许多形状不规则的物体,可能存在不同尺度上的相似性,称为自相似性。例如,皮兰(Perrin)于1908年用显微镜测量了布朗运动的轨迹,虽然实际的布朗微粒的轨迹是弯弯曲曲的曲线,但是他每隔30秒记录一次某个微粒的位置,再将相继得到的两点位置连成直线,得到如图4-1所示的一幅由长长短短的直线段连接成的轨迹图。他又将测量时间间隔缩短为每隔3秒,画出的另外一幅微粒的轨迹图。但将这两图进行比较一下可以发现,两幅图虽不尽相同,它们具有同等的复杂程度,前者可以看成为后者在尺度上的适当放大。实际上,这种两图之间在不同尺度上的相似性在还可以进一步扩展。例如,如果充许,我们可将记录微粒坐标的时间间隔延长到每隔数小时一次,或者缩短到每隔数毫秒一次。因此,记录的时间间隔跨度可以扩展到了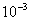 ~
~ 秒。而实验结果告诉我们,虽然记录时间间隔相差很大,但它们仍都具有相同的复杂性,因此,布朗微粒轨迹图存在自相似性。
秒。而实验结果告诉我们,虽然记录时间间隔相差很大,但它们仍都具有相同的复杂性,因此,布朗微粒轨迹图存在自相似性。
再如,人们在考察海岸线时发现,不管是漫步在海岸边看到的厘米量级的海岸线长度,还是从人造卫星上观察到的数千米跨度,海岸线的弯曲的复杂程度也可能是相同的。这种用不同尺度去测量都有相似的结果说明,这些测量对象没有特征尺寸,或者说它们具有尺度(标度)不变性。

图4-1 布朗微粒运动的径迹
基于测量对象体形上的自相似性与标度不变性,曼德布罗特提出了分形理论。首先,他在1973年在法兰商学院讲学期间提出了分形的几何学的基本思想,接着在1977年他出版了第一本著作:《分形对象:形、机遇与维数》,而在1982年出版了第二本著作:《自然界的形几何学》,从而奠定了这门新科学的基础。分形的英文词是“fractal”,是曼德布罗特创造的,用以表征某些不规则的几何形体。他给出的分形定义为: A fractal is a shape made of parts simslar to the whole in some way”,即“分形是其组成部分以某种方式与整体相似的图形”,或者说,分形是指一类体形复杂的体系,其局部与整体具有相似性。与人们熟悉的整规体形的整数维不同,分形体的维数不一定是整数,它可取连续变化的各种数值,称之为分形维数,或简称分维。根据分形体的不同特征,有多种分形维数的定义,而且由不同分形维数定义计算出的维数也有一些差别。
目前,分形的研究现已大大地超出了数学、物理学的范畴,它不仅广泛用于处理自然科学中相关问题,象雷电、相变、聚合物生长等等,而且在扩展到生态、生命、经济、人文的许多领域。在地震、气象的预报预测、石油的多次开采等应用领域,甚至在股票涨落分析等方面,分形也都得到了广泛的应用。由此可见,分形为人们处理复杂对象提供了一个强有力的工具。尤其值得一提的是虽然从表面上看来,分形似乎和前面讨论过的非线性动力学无多大关系,但是深入研究发现,分形与系统的混沌运动是密切相关的,它是非线性科学中的另一个重要分支。
第一节 豪斯道夫维数与规则分形
1. 豪斯道夫维数与相似维数
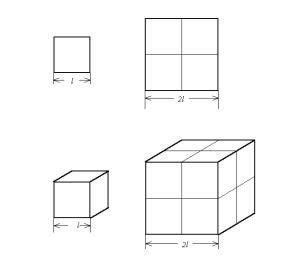
为了研究分形,首先来看一下数学家们是如何定义几何图形的维数的。我们考虑几个最简单的几何图形。取一个长度为l的线段,把它放大2倍,则放大以后的长度2l。一个边长为l的正方形,面积为l2,现在将每边长放大2倍,则放大后的面积为4 l2。一个边长为l的立方体,体积为l3,现在将每边长放大2倍,则放大后的体积为8 l3,如图4-2所示。于是,边长放大2倍前后的关系可以整理如下:
线段(一维图形) 
正方体(二维图形) 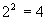
立方体(三维图形) 

图4-2 一个正方形的边长放大两倍,其面积放大四倍,
一个立方体的棱边放大两倍,其体积放大八倍
将边长放大的倍数记为L,放大后图形变化的倍数记为K,则上述关系可以表达为
显然,D即为相应图形的维数。对上式取对数,并将D记为 :
:
可以见到,对于正规的几何图形,(4-1-2)式的分子刚好可以为分母所整除, 为整数,这就是我们所熟悉的欧几里德维数。但对于不规则的几何图形,(4-1-2)式不总是可以整除的,于是在一般情况下,一个几何图形的维数是个分数,简称为分维。这就是说,规则几何图形是一般几何图形的特殊情况,与此相对应的整数维数也只是一种特例。这就是1919年由法国数学家豪斯道夫(Hausdorff)引进的分数维概念,
为整数,这就是我们所熟悉的欧几里德维数。但对于不规则的几何图形,(4-1-2)式不总是可以整除的,于是在一般情况下,一个几何图形的维数是个分数,简称为分维。这就是说,规则几何图形是一般几何图形的特殊情况,与此相对应的整数维数也只是一种特例。这就是1919年由法国数学家豪斯道夫(Hausdorff)引进的分数维概念, 常称为豪斯道夫维数。
常称为豪斯道夫维数。
我们还可以从另外角度来讨论图形维数的定义。例如,一个具有单位面积的正方形,现在把它等分成九个小正方形,即九个小正方形相加等于原来的面积,而这时小正方形的边长缩小为原来长度的1/3倍。上述关系为:
9×(1/3)2=1 (4-1-3)
显然式(4-1-3)中的指数2即为正方形的维数。实际上,式(4-1-3)表示了一种局部与整体的相似关系。因此,根据相似关系我们也可以来定义一个几何对象的维数。根据相似关系定义的维数称为相似维数 。我们假定某个几何体由N个局部所组成,每个局部以相似比β与整体相似,则此客体的相似维数
。我们假定某个几何体由N个局部所组成,每个局部以相似比β与整体相似,则此客体的相似维数 为:
为:
例如,我们考虑一个边长为2l的正方体,并将它四等分,得到四个边长皆为l的小正方形。对原正方形来说,小正方形是其局部,各小正方形彼此相同。经过平移或旋转操作,彼此可以重复。各小正方形的边长与原正方形边长之比为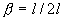 =1/2,即局部与整体的相似比为
=1/2,即局部与整体的相似比为 。用(4-1-4)式表达:
。用(4-1-4)式表达:
对于一个更复杂的几何对象,我们只要知道其局部与整体的相似比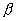 ,就可以计算其相似维数。然而相似维数
,就可以计算其相似维数。然而相似维数 与豪斯道夫维数
与豪斯道夫维数 虽然从不同的角度去定义的,但从计算结果看,两者是相等的。
虽然从不同的角度去定义的,但从计算结果看,两者是相等的。
2. 规则分形
现在来看一些比较特殊的几何图形,它们是在曼德布罗特提出分形理论之前,由许多数学家构造出来的一批具有自相似的几何图形,如康托尔(Cantor)点集,科赫(Koch)曲线,谢尔宾斯基(Serpinski)地毯等。这些数学家当时是从纯数学兴趣来构造这些图形,并称之为“病态图形”。现在采用分形理论去研究它们时,可以看到这些图形与正规几何图形之间存在着直接的联系。
2.1 康托尔点集
先介绍康托尔点集。取一线段[0,1]称为初始元,将其三等分,即各段的长度为原线段的1/3。取走中间一段,保留两侧的两段。将留下的两段再三等分,并再取走它们的中间一段,保留两侧的其余两段。照此继续的分割、取走下去,留下的线段愈来愈多,而其长度则愈来愈短,最终就分割成长度为无限短的无穷多个点,这些保留下来的分布开的点组成所谓三分康托尔点集。康托尔点集的所有点处于非均匀分布状态,具有自相似性,如图4-3所示。
图中 是康托尔点集的初始元线段[0,1]。
是康托尔点集的初始元线段[0,1]。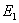 是生成元,它是由
是生成元,它是由 舍去中间1/3以后得到的,它包含[0,1/3]和[2/3,1]两个区段。
舍去中间1/3以后得到的,它包含[0,1/3]和[2/3,1]两个区段。 是分别舍去
是分别舍去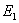 的两个区中的中间1/3后得到的,
的两个区中的中间1/3后得到的,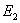 包含[0,1/9],[2/9,1/3],[2/3,7/9],[8/9,1]四个区段。按此规则继续操作下去,则生成元
包含[0,1/9],[2/9,1/3],[2/3,7/9],[8/9,1]四个区段。按此规则继续操作下去,则生成元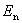 ,将由
,将由 个长度各为
个长度各为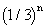 的区段组成。当
的区段组成。当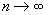 时,
时,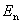 的长度l为
的长度l为
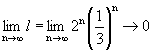
即随着线段分为无穷多段,不仅每段长度为零,其总长度也为零,因此构成了由无穷个点组成的点集。因为在组成中每次将线段一分为三,所以称康托尔三分集。依照康托尔点集的生成法则,我们可以生成四分、五分…等多种康托尔点集。例如在四分康托尔点集中,先将一线段四等分,再舍去中间两段,保留两侧的两段,以后再对保留的线段进行同样的操作。

图4-3 康托尔三分点集
现在计算康托尔三分点集的豪斯道夫维数。我们设想,每次三等分后的一小段,将此放大三倍,再把中间的1/3段舍去,得到两个1/3段,在豪斯道夫维数公式(5-1-2)中,L=3,K=2,因此有:
可见对于康托尔点集的0<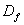 <1,说明它是介于点与线段之间的几何图形。
<1,说明它是介于点与线段之间的几何图形。
如用相似维数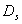 式(4-1-4)来计算时,则把康托尔点集的初始元线段长度作为1,生成元
式(4-1-4)来计算时,则把康托尔点集的初始元线段长度作为1,生成元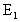 为两个1/3的线段,于是局部与整体的相似比β=1/3,N=2:
为两个1/3的线段,于是局部与整体的相似比β=1/3,N=2:
可见相似维数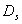 与豪斯道夫维数
与豪斯道夫维数 相等。
相等。
同样的方法可以计算康托尔四分点集的维数:
按照上面的操作方法,若把一线段进行n段等分,舍去中间的n-2段,保留两侧的两段,即构成n分点集,相应的维数为:
当n→∞时,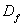 →0。表4-1给出了一些n与
→0。表4-1给出了一些n与 的对应数据。
的对应数据。
表 4-1 n与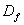 的对应数据
的对应数据
n
|
3
|
3.5
|
4
|
4.5
|
0.6309
|
0.5533
|
0.5000
|
0.4600
|
2.2 科赫曲线
科赫曲线是一种具有相似结构的弯弯曲曲的线段。它的构造过程如下:取一条长度为 的直线段,与构造三分康托尔点集那样先将它三等分,然后保留两侧的两段,将中间的一段改成夹角为
的直线段,与构造三分康托尔点集那样先将它三等分,然后保留两侧的两段,将中间的一段改成夹角为 的两个等长的直线,每段长度均为
的两个等长的直线,每段长度均为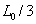 ,这是n=1的第一次操作。类似地,第二次操作是将上次所得的四段边长为
,这是n=1的第一次操作。类似地,第二次操作是将上次所得的四段边长为 的线段都进行三等分,现在每段长度为
的线段都进行三等分,现在每段长度为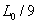 ,并将它们中间的一段改成夹角为
,并将它们中间的一段改成夹角为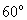 的两个长度为
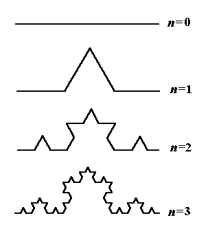
的两个长度为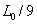 的直线。如果将上述操作一直进行下去,最终得到一条具有自相似结构的曲线,称为三次科赫曲线。图4-4是分别构造一次、二次和三次以后的图形。
的直线。如果将上述操作一直进行下去,最终得到一条具有自相似结构的曲线,称为三次科赫曲线。图4-4是分别构造一次、二次和三次以后的图形。
如图所示,三次科赫曲线由四个与整体相似的局部组成,相似比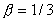 ,因此相似维数
,因此相似维数 为:
为:
可见对于三次科赫曲线,其维数1< <2,说明它是一种介于线段与面之间的几何图形。
<2,说明它是一种介于线段与面之间的几何图形。

图4-4 Koch 曲线
类似于科赫曲线的操作方法可以构造出一种所谓科赫雪花。以一个三角形作为源多边形,即初始元,将三角形的每一边做三等分,舍去中间的1/3,然后按科赫曲线的规则产生生成元。从源多边形开始,第一步形成一个六角星形,第二步将六角星形的12条边然后按科赫曲线的生成规则进行同样的操作得48条边星形,如图4-5,以后依此进行同样得操作,直至无穷,生成称为科赫雪花的图形。在极限的情况下,科赫雪花的上的折线演变成为曲线。由于科赫曲线生成中的每一步操作都会使折线的长度增加,所以在极限的情况下,科赫雪花边的总长度将趋于无穷:
然而,由于它是闭合的曲线,因此它所围的面积有一个确定的值,即:
计算表明,科赫雪花的分维数与科赫折线的维数 是相同的。
是相同的。

图4-5 Koch雪花的图形
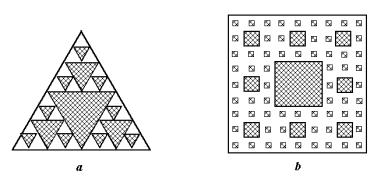
2.3 谢尔宾斯基图形
俄罗斯数学家谢尔宾斯基构造了一批千窗百孔的平面与立体图形。它们分别称之为谢尔宾斯基垫片、地毯及海棉等。
谢尔宾斯基垫片的构造方法是取一个等边三角形,将其四等分,得四个较小的三角形。然后舍去中间一个三角形,保留周围的三个三角形,如图4-6a所示。此后再将这三个较小的三角形按上述分割与舍去法则,进一步操作下去,得到一种介于线段与面之间的几何图形。因为对于此种图形可以设想从一个小三角形开始,将其每边扩大2倍,将得到与之相似的大三角形,其面积为小三角形的4倍。将约定中间的一个小三角形舍去,因此实际面积为小三角形的3倍。在豪斯道夫维数式(4-1-2)中,L=2,K=3,于是:
在构造谢尔宾斯基地毯时,取一正方形将其作9等分,得9个较小的正方形,并舍去中央的那个小正方形,保留周围的8个小正方形。然后将保留的每个小正方形再进行9等分,并且同样舍去中央的正方形,如图4-6b所示。按此规则不断细分与舍去,直至无穷。谢尔宾斯基地毯的极限图形面积趋于零,小正方形个数与其边的线段数目趋于无穷多,因此它实际上是一个线集,图形具有严格的自相似性。对于它的分维值,从考虑一个小正方形出发,将它的每边扩大三倍,并舍去中间的一个正方形,于是得豪斯道夫维数式(4-1-2)中的L=3,K=8,因此:

图 4-6 谢尔宾斯基垫片(a)与地毯(b)的前三次操作后的图形
我们还可以采用另一种方法来构筑谢尔宾斯基地毯。构成方法是取边长为1的正方形,按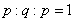 的方法划分每边,去掉中间的q部分,留下四角。然后对四角的小正方形进形类似的操作以至无限。图4-7是以
的方法划分每边,去掉中间的q部分,留下四角。然后对四角的小正方形进形类似的操作以至无限。图4-7是以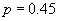 ,
,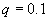 分割正方形操作五次以后的谢尔宾斯基地毯图形。显然每个小正方形与整体是相似的,即具有自相似性。按相似维数
分割正方形操作五次以后的谢尔宾斯基地毯图形。显然每个小正方形与整体是相似的,即具有自相似性。按相似维数 的计算公式,知是局部与整体的相似比β=2/9,N=4,得:
的计算公式,知是局部与整体的相似比β=2/9,N=4,得:
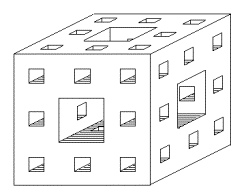
将上述的构造法则推广到空间就得到所谓谢尔宾斯基海棉。例如当将一个立方体的每边三等分后得到27个小立方体。将体心和面心上的共七个小立方体舍去保留其余的20个小立方体。下一步再对每个小立方体进行与上面一样的操作,这样就得到更小的20×20=400个立方体,结果如图4-8所示。将如此操作一直进行下去直至无穷。可以看出该图形的局部与其整体具有严格的自相似性,在极限情况下它的体积趋于零,而表面积趋于无穷大。因为当用3维的尺度去测量时体积为零,因此它实际上变成是一个面集,用2维的尺度去测量时面积为无穷大,它的分维值应介于2与3之间。

图 4-7 以 分割正方形在五次操作后的谢尔宾斯基地毯
分割正方形在五次操作后的谢尔宾斯基地毯
在具体计算谢尔宾斯基海棉的分维值时,可以考虑从其中一个小立方形出发,将每个棱边扩大三倍则体积放大27倍,由于舍去了七个体心和面心的小立方体,利用豪斯道夫维数式(4-1-2),得:
由此可见,对于谢尔宾斯基面集,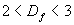 ,说明它是介于面与体积之间的几何图形。
,说明它是介于面与体积之间的几何图形。

图 4-8 谢尔宾斯基海棉两次操作后的图形
2.4 模拟分形物质
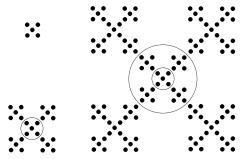
上述各种分形体都是数学家们设计出来的,现在讨论一个由物理或化学家们构造的一种模拟物质生长的自相似体,如图4-9。该种物质的构成方法如下:将一个半径为1的原子放在原点作为种子,然后在球的四个方向上再结合四个原子,这五个原子组成一个所谓晶胞。以下就是以晶胞为单位使物质由小到大生长起来。即以这个晶胞为中心,先在其四个原子的方向上结合上四个晶胞,再在四个晶胞的方向上结合上由五个晶胞结合成的集团。如此经过重复多次,就构成一块具有分形结构的宏观物体,这时二维情况。如果我们在一个原子的前后方向上又结合上两个原子,组成一个由七个原子组成的立体晶胞,就可以构成三维分形物体。
显然图4-9所示的结构也是一种规则分形体,因此可以计算出它的豪斯道夫维数。由图可见当线径放大L=3倍数时,其面积放大K=5倍数,应用豪斯道夫维数公式(4-1-2),得:

图4-9 以五个原子为晶胞的物质生长模型
第二节 容量维数、信息维数
从上面讨论中看到,采用豪斯道夫维数的计算方法,可以方便地计算出由数学家们创造的严格的自相似图形。一般来说,如果已知某个分形体的自相似比,就可以以采用豪斯道夫维数的计算方法计算其维数。但是大自然中存在的是大量的在统计意义下的自相似体,它们的自相似比往往并不知道。这时采用上面的豪斯道夫维数方法来计算其分形维数就比较困难了,为了解决这个问题,人们发展了一种计算容量的分维计算方法。
1. 容量维数与信息维数
对于一个复杂的几何图,当我们无法知道其局部与整体之间的相似比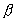 时,可以采用一个小方块(或圆片)去覆盖(或填充)被测对象,并通过统计覆盖所需的小方块数来计算其维数,这种方法称为盒子计数法(box counting)。用这种方法计算出的维数称为容量维数
时,可以采用一个小方块(或圆片)去覆盖(或填充)被测对象,并通过统计覆盖所需的小方块数来计算其维数,这种方法称为盒子计数法(box counting)。用这种方法计算出的维数称为容量维数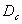 。
。
设想我们用一根长度为r尺寸去测量长度为L的线段,测得L与r之比值为N。显然N值的大小与r的长短有关,显然r越小 越大,即:
越大,即:
如果被测物是一块平面上,则用边长为r的方块去覆盖时应有:
当被测物是立体时,我们用线径为r的小球去填充,可得N(r)数为:
显然上述各式中的指数1、2与3分别为线段、平面与立体的维数。
将上述的讨论加以推广,对于一个维数为 的物体当用线度为r的盒子去覆盖时,可得的
的物体当用线度为r的盒子去覆盖时,可得的 数为:
数为:
一般来说为了精确测量一个不规则物体,所用的尺子越短越精确,在极限情况下有:
对式(4-1-13)取对数得容量维数 :
:
由于在实际计算某个分形体的容量维数时,我们不可能取长度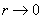 的比例尺去测量,常用的方法是用几个有限长度的比例尺进行多次,并将测量结果作logN~logr双对数图。如果测量对象确是分形体,便得一条负斜率的直线,其绝对值就是它的分维值
的比例尺去测量,常用的方法是用几个有限长度的比例尺进行多次,并将测量结果作logN~logr双对数图。如果测量对象确是分形体,便得一条负斜率的直线,其绝对值就是它的分维值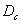 。
。
作为例子我们用盒子计数法来计算图4-9所示的物质模型的容量维数。可设晶胞重复结合了P次,则该物质的线径为 ,而包含的原子数应有
,而包含的原子数应有 个。现在用线径为
个。现在用线径为 的小球去覆盖,可得:
的小球去覆盖,可得:
由式(4-2-3)得:
可见对于如此构造的规则物质,其容量维数与豪斯道夫维数是相等的,即: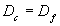 。
。
容量维数计算很直观、很实用。例如我们可以用来计算奇怪吸引子的维数。图4-10是用边长为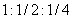 的三种方块去覆盖埃侬吸引子的情况。当我们用边长为1的方块去覆盖时需用35块;当用边长为1/2的方块去覆盖时需用95块;当用边长为1/4的方块去覆盖时需用220块。我们还可以用边长更短的方块去覆盖,并用式(4-2-3)去计算其维数,实际计算可得埃侬吸引子维数为1.26。
的三种方块去覆盖埃侬吸引子的情况。当我们用边长为1的方块去覆盖时需用35块;当用边长为1/2的方块去覆盖时需用95块;当用边长为1/4的方块去覆盖时需用220块。我们还可以用边长更短的方块去覆盖,并用式(4-2-3)去计算其维数,实际计算可得埃侬吸引子维数为1.26。

图4-10 用不同边长r的方块覆盖埃侬吸引子
然而用上述的盒子计数法计算容量维数时,往往反映不出客体分布上的不均匀性,因为对象的不均匀性将使不同的计数盒子有不同的填充程度,因此人们改进了上述的分维盒子计数法,改进以后计算出的维数称为信息维数。其方法是先统计出分形结构落入第 i只盒子的几率  ,并以概率
,并以概率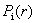
来反映第i个盒子中的填充程度。再利用信息公式:
定义信息维数
显然当各个盒子具有同样的填充程度时,
信息维数就等于容量维数, =
= 。而在一般情况下
。而在一般情况下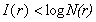 ,因此
,因此
2. 布朗运动
布朗运动是另一类具有自相似性的例子,称为统计自相似性。因为如图4-1所示的布朗运动的轨迹线是其无规行走的结果。无规行走的名称来自于醉汉的不自主行走,他的每走一步的方向都是任意的,因此其行走路线迂回曲折。布朗运动无规行走的物理原因是液体中周围分子对微粒撞击造成的瞬时涨落。
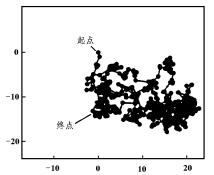
由于布朗微粒在行走中迂回曲折,因此虽经长时间行走,离起点距离不会太远,理论计算表明实际的行走距离正比于时间t的方根,即 。图4-11是从坐标的原点出发行走了500步的线路图。
。图4-11是从坐标的原点出发行走了500步的线路图。

图4-11 无规行走图
我们如何来计算布朗微粒运动的分形维数呢?取某一瞬时位置为坐标原点,计算粒子走了N步以后离原点的距离。粒子的总位移矢量R应是它的每一步的位移矢量r的矢量和,即:
因为空间是对称的故〈R〉=0,因此需要用总位移的均方根R的平方来度量布朗微粒的轨迹,即:
由于布朗运动的随机性,每一步的位移矢量都是独立的,所以上式右边的第二项为零。设第一项中每步位移的平均值为b,则得:
式(4-2-7)是步数N与无量纲约化总位移之间的关系式。该式说明,在总位移一定的情况下,如果平均位移b很小,则测量的次数N就要增多。对式(4-2-7)取对数,得:
或者:
 .
.
按容量维数的定义有:
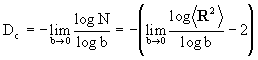 (4-2-8)
(4-2-8)
上式右边第一项在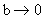 时趋于零,于是得布朗运动的分维为:
时趋于零,于是得布朗运动的分维为:
以上的推导适合于多维的空间,即无论布朗运动是一维的、二维的或是三维的,其分维数都为2。一维运动怎么会走出二维的图形?其原因就在布朗运动的路线是迂回曲折的。在一维情况下,布朗粒子将沿着直线来回不停地行走,造成一维线段上走出了二维的图形,然而更高维数的运动空间又没有使分形维数增加,这是一种十分有趣的现象。
3. 自然界分形
大自然中存在着非常多分形体。不论是一座座山脉,一片片树林,或是瞬间即逝闪电,弯弯曲曲海岸线,都可能包含着各种形式的自相似性,它们一般不大可能是规则的,应属于无规分形。这里以海岸线为例,分析一下存在于自然界中的分形体。
弯弯曲曲的海岸线为什么是分形体?首先是它具有自相似性。当我们从不同的高度来观察一段海岸线时,可以发现,虽然因视场不同从不同高度观察所看到的范围不一样,但它具有同等的复杂程度。这是大自然力量造就的杰作。其次,如果以不同比例尺的标尺去测量,所得到的海岸线长度是不同的,小比例尺测量出的长度长,大比例尺测量出的长度短,其原因在于用大比例尺时会忽略掉更多的弯曲细节。我国的海岸线北起中朝边界的鸭绿江口,南止中越边界的北仓河口,全长一万八千余公里。这个长度是以1公里长的标尺测量得到的。实际上,如果以1公里为测量单位,所测得海岸线有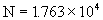 段。然而如果我们采用短一些的标尺,例如1厘米长的标尺,则测得海岸线就有
段。然而如果我们采用短一些的标尺,例如1厘米长的标尺,则测得海岸线就有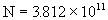 段,可以算出这时的长度为381.2万公里。这是地理书上给出长度的212倍。
段,可以算出这时的长度为381.2万公里。这是地理书上给出长度的212倍。
计算一段海岸线的维数通常可以采用两种方法:一是用不同边长r的方格去覆盖,统计出覆盖这段海岸线的格子数目,然后对其中某个方格的海岸线进行放大,并用另外边长小一些的方格去覆盖统计出这次覆盖的格子数目,如此继续进行类似的操作,用边长更小的格子去覆盖再放大的一段海岸线,于是就得到一组与格子边长相对应的格子数目 ;另一种是在地图上以不同长度r的标尺去测量海岸线,可以得到一组与该标尺长度对应的段数
;另一种是在地图上以不同长度r的标尺去测量海岸线,可以得到一组与该标尺长度对应的段数 。两种方法都可以使用容量维数式:
。两种方法都可以使用容量维数式:
来计算。将测量结果作logN~logr双对数图得一负斜率的直线,其绝对值就是维数 。如果得到的图不是一条直线,说明此段海岸线没有分形特征。
。如果得到的图不是一条直线,说明此段海岸线没有分形特征。
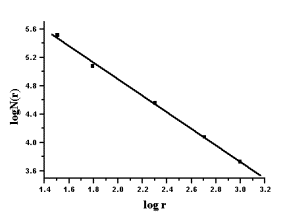
有人曾用不同比例尺在地图上对我国海岸线进行过测量,测量的有关数据如表4-2所列,用表中数据所作的logN~logr曲线得如图4-12所示的斜线。由图可见,所得的斜线基本上是直的,其方程可以写为:
式中的系数1.267就是该直线的斜率,即海岸线的分维值为:

图4-12 我国海岸线分维计算的logN~logr曲线
表4-2 用盒子计数法进行我国海岸线分维计算的有关数据
r(mm)
|
N
|
Log r
|
Log N
|
20
15
10
6.0
4.5
2.5
|
41.7
58.9
95.4
160.1
248.5
596.0
|
2.996
2.708
2.303
1.792
1.504
0.916
|
3.731
4.076
4.558
5.076
5.515
6.344
|
第三节 时序分析与关联维数
1. 时序分析
前面我们在研究动力学系统时已经提到,当一个动力学体系进入混沌状态后,它的某些行为,例如分岔图、相图、奇怪吸引子结构等等,具有自相似性特性。然而当我们从实验上研究一个动力学系统时,通常是按一定的时间间隔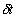 去测量系统的某些变量的。通过测量,我们获得的是一组数据。如何从这组数据中获取动力学运动的信息呢?这节就是讨论这个问题。
去测量系统的某些变量的。通过测量,我们获得的是一组数据。如何从这组数据中获取动力学运动的信息呢?这节就是讨论这个问题。
设由测量获得的数据为:
这里, 是在时刻t测量得到得数据。
是在时刻t测量得到得数据。
我们知道,分形的对象是空间几何体。那么我们如何从测量数据中获得系统的分形信息呢?一个方法是利用测量数据构筑一个抽象空间,称为嵌入空间,其意思是测量数据嵌入在这样的空间内。然后再对这样的空间作分形分析。
为了构筑嵌入空间,可以事先设定一个它的维数,例如设定维数为p,于是由测量数据得一序列:
这里,g称嵌入间隔。由此可见每个 就是p-维嵌入空间中的一个点,每一时刻t一个点,每个点代表了系统在该时刻的状态。而整个测量数据构成空间的点序列。
就是p-维嵌入空间中的一个点,每一时刻t一个点,每个点代表了系统在该时刻的状态。而整个测量数据构成空间的点序列。
举一个洛仑兹方程的时间系列分析的例子。取洛仑兹方程组中的参数为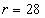 ,
,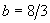 ,
,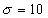 ,这样的参数是洛仑兹方程出现奇怪吸引子的条件,则方程组为:
,这样的参数是洛仑兹方程出现奇怪吸引子的条件,则方程组为:

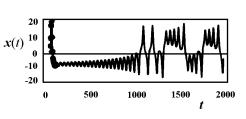
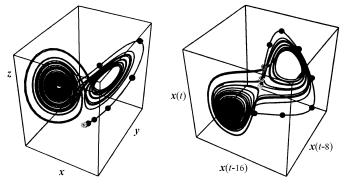
图4-13是对洛仑兹方程的 分量测量的时间系列图。图4-14a是在
分量测量的时间系列图。图4-14a是在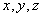 三维相空间中洛仑兹方程的图象。现在取嵌入间隔
三维相空间中洛仑兹方程的图象。现在取嵌入间隔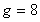 ,则得三维嵌入空间的坐标为
,则得三维嵌入空间的坐标为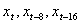 ,在此嵌入空间内的图象如图4-14b所示。通过比较图4-14a与图4-14b可以见到,虽然两图的轨线行走不尽相同,但它们都显示出了洛仑兹方程的奇怪吸引子。
,在此嵌入空间内的图象如图4-14b所示。通过比较图4-14a与图4-14b可以见到,虽然两图的轨线行走不尽相同,但它们都显示出了洛仑兹方程的奇怪吸引子。

图4-13洛仑兹方程x分量时间系列

a b
图4-14洛仑兹方程x分量时间系列
为了计算由时间系列包含的动力学信息,需要引进关联积分的概念。首先在构筑好嵌入空间以后,计算在两个时刻i与j点间的距离:
显然,如果时间系列是以T为周期的,当 时,
时, ,则
,则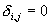 。而对于非周期的时间系列,
。而对于非周期的时间系列, 不满足这样的条件。
不满足这样的条件。
我们事先设定某个距离值r,并检查两点间距离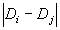 与设定值r的对比。凡是
与设定值r的对比。凡是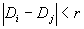 ,则称两点是相关的,否则为不相关的。两点间是否相关可以通过图象表示出来。其作法是以i为横坐标,j为纵坐标,检查
,则称两点是相关的,否则为不相关的。两点间是否相关可以通过图象表示出来。其作法是以i为横坐标,j为纵坐标,检查 的大小,如果出现
的大小,如果出现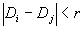 ,就在的(i,j)的坐标平面上打上一个点,因此在平面上出现由
,就在的(i,j)的坐标平面上打上一个点,因此在平面上出现由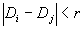 的所有点构成的图样。由这样方法作出的图称为重现图,图上的点的数目告诉我们,轨道有多少次来到了我们事先设定的距离之内。因此重现图描述了重构轨道的再现情况。
的所有点构成的图样。由这样方法作出的图称为重现图,图上的点的数目告诉我们,轨道有多少次来到了我们事先设定的距离之内。因此重现图描述了重构轨道的再现情况。

a. 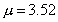 b.
b. 
图4-15 平方映射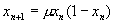 的轨道重现图
的轨道重现图
图4-15是平方映射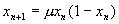 在不同
在不同 值时的轨道重现图。图4-15a是
值时的轨道重现图。图4-15a是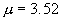 的情况,这时映射为周期4轨道。设嵌入空间的维数p = 2,设定距离r = 0.001,重现线是45度角的直线,因为直线条间的水平间距与垂直间距都为周期T = 4。如果增加设定距离r,例如增加十倍r = 0.01,实验结果表明重现图与r = 0.001的情况相同。图4-15b是
的情况,这时映射为周期4轨道。设嵌入空间的维数p = 2,设定距离r = 0.001,重现线是45度角的直线,因为直线条间的水平间距与垂直间距都为周期T = 4。如果增加设定距离r,例如增加十倍r = 0.01,实验结果表明重现图与r = 0.001的情况相同。图4-15b是 的情况,这时仍设嵌入维数p = 2,设定距离r = 0.001,可见重现线虽然仍为45度,但不再是平行的直线条,而是许许多多长短不一的线段构成的图,因为
的情况,这时仍设嵌入维数p = 2,设定距离r = 0.001,可见重现线虽然仍为45度,但不再是平行的直线条,而是许许多多长短不一的线段构成的图,因为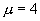 对应着平方映射处在混沌状态。当设定距离r增加时,例如增加十倍,对于一个有混沌特征的时间系列,其重现图形的结构将会显得非常复杂。
对应着平方映射处在混沌状态。当设定距离r增加时,例如增加十倍,对于一个有混沌特征的时间系列,其重现图形的结构将会显得非常复杂。
2. 关联维数
由两点的相关性可以定义一个相关积分。它是i与j两时刻间对的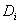 与
与 小于r(
小于r( )所占的百分比,即:
)所占的百分比,即:
式中分子上的指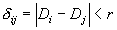 的所有时刻对的点数目,而分母上的最大可能的点数
的所有时刻对的点数目,而分母上的最大可能的点数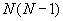 是去掉了
是去掉了 这种情况,当N很大时,分母上的实际数为
这种情况,当N很大时,分母上的实际数为 。
。
现在讨论一下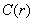 与r之间的关系。根据
与r之间的关系。根据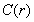 的定义,可以定性地看出,
的定义,可以定性地看出,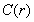 是随r的增加而增加的。但是
是随r的增加而增加的。但是 随r增加而增加的趋势与运动状态有关。在系统作周期运动情况下,例如平方映射,当
随r增加而增加的趋势与运动状态有关。在系统作周期运动情况下,例如平方映射,当 作出4周期运动,如图4-15所示,这时r = 0.001与 r = 0.01的重现图是同样的。这就是说,系统作周期运动的情况下
作出4周期运动,如图4-15所示,这时r = 0.001与 r = 0.01的重现图是同样的。这就是说,系统作周期运动的情况下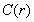 随r的增加实际上是不变的,或者说变化是很慢的。与此不同,当
随r的增加实际上是不变的,或者说变化是很慢的。与此不同,当 平方映射中作混沌运动时,如图所示
平方映射中作混沌运动时,如图所示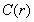 是随r的增加而单调增加的。
是随r的增加而单调增加的。
可以发现图4-15b所示的图象是一个具有分数维的分形图象。实际上当动力学体系进入混沌状态后,它的某些行为例如奇怪吸引子具有自相似性特性。在时序分析中,混沌状态的自相似性也应在重现图上表示出来。于是我们就可以利用重现图来计算系统的分形特性。
因为重现图与关联积分有关,用重现图计算出的分形维数称为关联维数。计算方法与与上节的容量维数的计算方法基本相同。按容量维数计算思想,一维曲线上散落在尺度r内的点数比例于r一次方,二维平面上散落尺度r内的点数比例于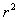 ,三维体积内散落尺度r内的点数比例于
,三维体积内散落尺度r内的点数比例于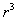 ,与此同理,对于维数为
,与此同理,对于维数为 的重现对象,散落在尺度r内的点数
的重现对象,散落在尺度r内的点数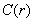 比例于
比例于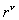 ,即有:
,即有:
式中A是比例常数。对上式的两边取对数,
取不同的r值对上式作图得一直线,直线的斜率即为所要求的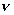 。
。
现在需要分析一下如何选取嵌入空间的维数p。关联维数常用于分析奇怪吸引子的分维计算。塔肯斯曾经证明,如果原吸引子的维数为 ,则需取嵌入空间的维数
,则需取嵌入空间的维数 来重构吸引子。但是实际工作中,吸引子的维数
来重构吸引子。但是实际工作中,吸引子的维数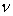 正是需要计算得到的,事先并不知道。在这种情况下,可以从小到大取数个p值,并由关联积分计算维数
正是需要计算得到的,事先并不知道。在这种情况下,可以从小到大取数个p值,并由关联积分计算维数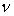 ,并作
,并作 曲线,可以发现,开始时
曲线,可以发现,开始时 随p的增加而增加,以后逐渐变慢以至恒定,这就是所要求取的维数
随p的增加而增加,以后逐渐变慢以至恒定,这就是所要求取的维数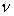 。
。
第四节 分形生长
1.散置限聚集模型
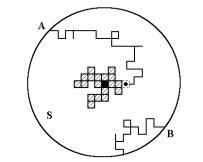
在大自然中,在自然科学的各学科领域,都存在大量的分形客体。各种分形客体是怎样形成的?在形成过程中存在着那些物理学的、化学的、生物学的或其它的动力学过程?这是研究分形产生规律中提出的一个重要课题。为此许多分形研究工作者提出过各种分形产生模型,但是鉴于实际分形体的复杂性与多样性,不同的理论模型但往往它们只能说明某些特定的分形体,只用一种理论模型一般不大可能去解释各种实际的分形对象。在各种分形生长模型中,由魏滕(Witten)和山特(Sander)提出的一种扩散置限聚集模型(diffusion-limited aggregation,简称DLA模型)是一种影响比较大,有代表性的分形生长理论模型。该模型于1981年提出后,1983年又研究了模型与扩散方程的关系,进一步完善了这个模型。这里对该模型的思想作一些简单介绍。
DLA是针对生长过程出现的无规分形提出的。按照这个模型,一种无序的、不可逆的生长过程可以产生一种特殊的分数维体形。该模型是在计算机上模拟完成的,如图4-16所示。它的生成过程是这样的,先在一个二维点阵的中心放上一棵粒子称为种子,即图中心的黑色单元,然后在点阵的边缘引进一棵粒子,如图中的A或B,让它在二维点阵上随机地游荡。当该粒子游动到点阵的中心附近时,它将与位于中心点的种子相结合(A粒子),于是附着就不动了;或者该粒子游动到点阵的边缘,于是会消失掉(B粒子)。不管出现哪种情况,点阵上一旦失去了游动的粒子,需要从点阵的边缘再引进一棵新的游动的粒子,也就是说,在点阵上需要始终保持有游动的粒子存在。新粒子在点阵上游动又会发生上述两种情况:或者游动到点阵中心附近与附着不动的粒子相结合,或者游动到点阵的边缘而消失,于是再从边缘引进新的粒子。如此不断地从边缘引进粒子,点阵中心将逐渐出现一个粒子的聚集集团,即图中那些在黑色单元周围的阴影单元。由于新粒子在聚合以前是通过随机行走扩散到该聚集体的,在随机行走的过程中,每一步的幅度与方向都是随机确定的,这就是所谓扩散置限聚合名称的来历。

图4-16 扩散置限聚集分形生长模型
这种聚集集团的生长的特点是具有屏蔽性,即新的粒子只能在聚集体的外缘结合上去,不能深入到内部的某些孔隙的地方结合。因此结合起来的聚集体具有象树枝状的松散结构,如图4-17a所示。研究证明,DLA集团具有统计意义上的自相似性。就是说,以分形体内的任一点为中心,取不同的半径r作圆,则包含在圆内的聚集粒子数 与r的关系可以写为:
与r的关系可以写为:
这里的D就是DLA聚集集团的分形维数。大量的研究表明,分形维数D通常在1.6~1.7之间。

a b c
图4-17 DLA聚集集团的分形图像
用扩散限制聚合模型可以说明许多物质生长现象。例如将一根铁丝的表面镀上一层锌,如果电镀过程的参数(如溶液浓度、电流大小等)控制不好,表面锌镀层会很不光滑,镀出相图4-18b样的松散结构。图4-18c是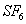 绝缘气体中在玻璃板面上放电的摄影图象。
绝缘气体中在玻璃板面上放电的摄影图象。
2.粘性指进
近年来一种称为粘性指进(viscous fingering)的分形现象受到了人们的重视。这是一种类似于水在油中流动实验所出现的现象,可以用DLA模型来解释。早在十九世纪,有一位名叫海尔-肖(Hele-Shaw)的英国造船工程师做了这样的实验。实验是两块具有一定间隔平躺着的平板玻璃间进行的,称为海尔-肖盒,平板玻璃内充粘度较大的液体,例如甘油,四周敞开。在上玻璃板中央有一小孔,从中注水(或空气等小粘度流体)。海尔-肖发现在压力的驱动下,水在甘油中并非均匀地向四周扩散开来,而是呈张开的手指形状那样四散地游动如图4-18所示,这便是“粘性指进”名称的来历。
为什么水在油中呈手指形状游动呢?原来当水在油中游动时,水-油之间的界面受到很大的压力,水的游动是界面压力平衡的结果,好似一个手指顶向一块橡皮薄膜那样,被手指顶住的地方,受力最小。当油从海尔-肖盒四周外溢时,压力减小,水就以手指状的方式向四周扩散开来。分析表明,粘性指进现象具有分形体的性质,并类同于扩散制限聚合的生长方式发展。
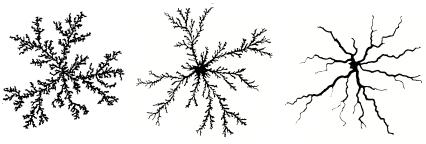
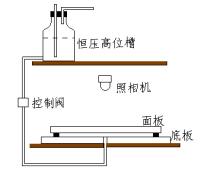
粘性指进的实验装置颇为简单,人人可做。图4-19是一种研究粘性指进的实验装置。取两块平板玻璃(可圆可方),其中一块可以大些(如40厘米见方)称作底板,另一块小些(如30厘米见方)作面板。用几个垫脚将面板玻璃板支架在底板玻璃上,两者之间的间隙约0.5~1毫米,根据需要可以调节。这便是以海尔-肖命名的海尔-肖盒。为了研究不同条件下的粘性指进图形,可在面板上方置一照相机以便拍摄图象。这样需在底板中心钻一小孔(约2毫米直径)用于注水,为使图象清晰,注入的水应是染色的。实验时在海尔-肖盒中充上所需研究的高粘性液体,如甘油、原(石)油、香豆胶水溶液之类。然后通过底板上的小孔对海尔-肖盒注水。实验中注水的压力应是恒定的,图4-19中的恒压高位槽就是起这样的作用。
由于粘性指进现象与现代的石油开采有密切关系,所以近年来对它的研究很受重视。原来在采石油中,在经过一段时期的初期开采以后,随着地层内部压力的下降,地下还有一定数量的石油就取不出来了。最初想到的办法是向地下注水,根据水的比重大油的比重小,水将下沉到底部的道理,剩余在地层内的石油应该能托向地面。可是事与愿违,在压上来的油中含有大量压下去的水。究其原因就在于水在油中流动时是以粘性指进方式前进的。


图4-18 粘性指进 图4-19 粘性指进实验装置
第五节 动力学与分形
1. 奇怪吸引子的分形维数
第二章在对奇怪吸引子作介绍时曾经指出,奇怪吸引子具有自相似的分形结构。以埃侬吸引子为例,取埃侬映射参数m=1.4,b=0.3通过计算机编程计算,可在(x,y)相平面上得到如图4-23a所示的图形,粗看犹似一只弯曲香蕉,其‘香蕉’头处显出三条弯线。现在对‘香蕉’头取个小方块,对顶部那条线进行精细一点的计算,得到图4-23b那个放大一点的图形,可见其头部不是简单的一条曲线。为了进一步显示其结构,再对图4-23b顶部的条线进行放大,就得到图4-23c图,可见大致分成了三层曲线,顶层有三条,中间层有两条,下层为单线的结构图形。现在进一步再对图4-23c上的顶层三条线进行局部放大,则更细致的图形如图4-23d显示出来了。通过比较图4-23c、d两图可见,不论进行多少次逐步放大,顶层的每一条线都将给出三层结构,说明局部与整体是相似的,埃侬吸引子具有分形特性。其实,如果对其它一些奇怪吸引子,如洛仑兹吸引子,罗斯勒吸引子等等进行类似的分析,均可以发现它们都具有分形结构。奇怪吸引子的相轨线虽然由于永不重复而非常稠密,但它们不可能填满所存在的全部空间空间,因此维数就不会是整数。实际上奇怪吸引子的维数是其复杂性的几何测度,是描述奇怪吸引子的一个重要参数。
表4-3列出了几个常见的典型奇怪吸引子的分形维数。

图 4-20 四种不同标度下的埃侬吸引子
表4-3 几个常见奇怪吸引子的分形维数
模 型
|
参 数
|
维 数
|
洛仑兹模型
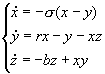 |
2.04
| |
罗斯勒模型
 |
2.014
| |
埃侬模型
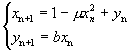 |
1.20
1.26
| |
布鲁塞尔模型
 |
2.15
| |
蔡氏模型
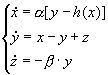 |  |
2.13
|
如何计算奇怪吸引子的分形维数?从奇怪吸引子图形与特征,采用不同分形维数的计算方法,可以分别计算出它们的容量维数、相似维数及相关维数等。此外,一个动力学系统存在奇怪吸引子,表明它对初始条件极端敏感性。这个特性常用一个正值的李雅普诺夫指数来描述。那么奇异吸引子的分形维数与其李雅普诺夫指数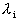 之间是否存在着什么样的关系呢?现在就来讨论这个问题。
之间是否存在着什么样的关系呢?现在就来讨论这个问题。
不失一般性,我们考虑一个二维映射用来计算两个李雅普诺夫指数 的吸引子的容量维数。覆盖时共用了
的吸引子的容量维数。覆盖时共用了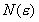 块边长为
块边长为 正方块。对该映射进行q次迭代,在q固定和
正方块。对该映射进行q次迭代,在q固定和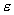 值足够小时,映射操作可以看作为线性的。由于两个指数
值足够小时,映射操作可以看作为线性的。由于两个指数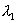 与
与 不同,初始的每一个小方块将拉伸成平行四边形,如图4-21(b)所示。平行四边形的平均边长是
不同,初始的每一个小方块将拉伸成平行四边形,如图4-21(b)所示。平行四边形的平均边长是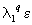 ,平均宽度是
,平均宽度是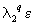 。假设现在再使用边长为
。假设现在再使用边长为 小方块,那么为了复盖每个平行四边形,就要用
小方块,那么为了复盖每个平行四边形,就要用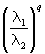 个更小的正方块。根据这样的操作,吸引子上的所有正方形数约为:
个更小的正方块。根据这样的操作,吸引子上的所有正方形数约为:
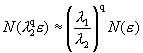 (4-5-1)
(4-5-1)
图 4-21 李雅普诺夫维数的计算
根据分形维数定义,假定
或者写成等式
式中m是一个比例系数。将上式分别代入(4-5-1)式的右边与左边,得:
 (4-5-2)
(4-5-2)
消去等式两边相同的系数:
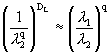
取对数,

整理得:
因此如果我们已经知道了某个奇异吸引子的李雅普诺夫指数,就可以通过式(4-5-3)计算出它的分形维数。为了与前面定义的维数有所区别,把这里推导得到的维数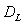 称为李雅普诺夫维数。把上述讨论推广到指数为
称为李雅普诺夫维数。把上述讨论推广到指数为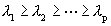 的P维映射,由式(4-5-3)得:
的P维映射,由式(4-5-3)得:
这里k是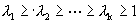 的最大值。如果
的最大值。如果 ,定义
,定义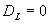 ,如果
,如果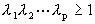 ,则定义
,则定义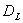 =P。
=P。
2. 奇怪排斥子与康托尔点集
在非线性动力学中,除存在奇怪吸引子外,还存在一种奇怪排斥子。为了了解奇怪排斥子,我们再研究一下对平方映射:
在以前的迭代计算中,总是将控制参数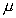 值限制在
值限制在 的范围内,因此,当
的范围内,因此,当 处在
处在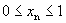 内取值时,迭代产生的
内取值时,迭代产生的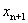 也总落在[0,1]范围之内。然而,如果我们突破对参数
也总落在[0,1]范围之内。然而,如果我们突破对参数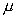 取值的限制,考虑
取值的限制,考虑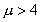 的情况,则通过运算可以发现,即使
的情况,则通过运算可以发现,即使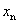 仍在
仍在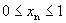 内取值,但只要再经过两次迭代,
内取值,但只要再经过两次迭代,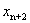 就可能超出[0,1]的范围,甚至
就可能超出[0,1]的范围,甚至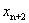 可能变成负值。这个结果也可以从如下的分析中得到:由于
可能变成负值。这个结果也可以从如下的分析中得到:由于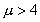 ,因此如取
,因此如取 ,一次迭代
,一次迭代
就大于1,二次迭代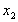 将为负:
将为负:
而且可以发现,一旦出现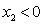 ,余下的继续迭代所产生的值
,余下的继续迭代所产生的值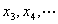 都将小于零,并逐渐走向于
都将小于零,并逐渐走向于 。人们将这种现象称为逃逸。
。人们将这种现象称为逃逸。
现在来分析另一种称为帐篷映射的动力学模型中的逃逸现象。帐篷映射的图象因象汉字“人”字,所以也称人字映射,它可以写为:
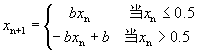 (4-5-5)
(4-5-5)
式中b为控制参数。计算表明,当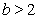 时帐篷映射的可以产生
时帐篷映射的可以产生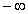 逃逸。下面以
逃逸。下面以 为例进行分析。如图4-22所示,
为例进行分析。如图4-22所示,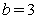 时帐篷映射有两个不动点:
时帐篷映射有两个不动点:
从前面平方映射的稳定性讨论中知道,一个动力学系统的不动点的稳定性条件是在不动点处映射的斜率m满足 。对于
。对于 的帐篷映射来说,两个不动点的斜率m分别为
的帐篷映射来说,两个不动点的斜率m分别为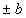 ,即3与
,即3与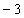 ,显然已超出了不动点的稳定性要求,因此它们是不稳定的不动点。由于不动点是不稳定的,因此只要初始条件存在某种很小的偏离,系统就象受到排斥一样,迅速离开不稳定轨道而出现逃逸现象,人们称之为奇怪排斥子。
,显然已超出了不动点的稳定性要求,因此它们是不稳定的不动点。由于不动点是不稳定的,因此只要初始条件存在某种很小的偏离,系统就象受到排斥一样,迅速离开不稳定轨道而出现逃逸现象,人们称之为奇怪排斥子。

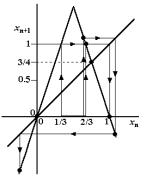
图4-22 帐篷映射上的迭代
就象奇怪吸引子具有分形结构一样,奇怪排斥子也具有分形特征。通过作图迭代可以看到, 的帐篷映射在迭代中有一些有趣的逃逸现象:首先当起始点
的帐篷映射在迭代中有一些有趣的逃逸现象:首先当起始点 取在区间[1/3,2/3]内的任一点时,都将产生向
取在区间[1/3,2/3]内的任一点时,都将产生向 的逃逸;其次当起始点
的逃逸;其次当起始点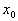 在区间[0,1]内除取区间[1/3,2/3]外的其余点时,如果在经过数次迭代后也进入到[1/3,2/3]区间之内时,也会在后继的迭代中产生向
在区间[0,1]内除取区间[1/3,2/3]外的其余点时,如果在经过数次迭代后也进入到[1/3,2/3]区间之内时,也会在后继的迭代中产生向 的逃逸。由此可见在[0,1]内的点只有少数可以“存活”下来。假设在区间[0,1]内取
的逃逸。由此可见在[0,1]内的点只有少数可以“存活”下来。假设在区间[0,1]内取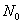 个初值为起始点,如果在经过n次迭代后还有
个初值为起始点,如果在经过n次迭代后还有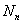 个点没有逃逸,则可以预计Nn将随迭代次数的增加而指数地减少,即:
个点没有逃逸,则可以预计Nn将随迭代次数的增加而指数地减少,即:
式中指数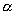 称为逃逸速率。
称为逃逸速率。
我们称经过经过一次迭代后不产生逃逸的点为存活1,而将区间[0,1]内的所有点称为存活0。显然,对于参数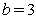 的帐篷映射来说,在[0,1]的单位长线段上,除区间[1/3,2/3]外,所有的点都属于存活1,因此一次迭代后点的存活概率p为:
的帐篷映射来说,在[0,1]的单位长线段上,除区间[1/3,2/3]外,所有的点都属于存活1,因此一次迭代后点的存活概率p为:
经过n次迭代后仍然存活的概率为:
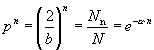 (4-5-7)
(4-5-7)
由式(4-5-7)可以求得逃逸速率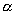 为
为
通过如此计算可以发现,对于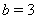 的帐篷映射,其全部的存活点集构成了一个理想的康托尔三分集。已知存活2是由经过两次迭代不产生逃逸的点构成,它可由存活1得到。而由图4-23可知,帐篷映射由上行与下行的两段斜线构成,于是可以用作图的方法由存活1得到存活2。以存活1的点集作纵坐标,存活2的点为横坐标,则存活2的点集可以由帐篷映射的两段斜线作镜像反射从存活1的点来获得。推而广之,我们可以从存活2推导出存活3,进而可以从存活n-1推导出存活n。参照康托尔三分点集图4-3,可以将初始康托尔元看成是由存活(0)的点构成的。一次迭代后留下的存活(1)的点构成生成元
的帐篷映射,其全部的存活点集构成了一个理想的康托尔三分集。已知存活2是由经过两次迭代不产生逃逸的点构成,它可由存活1得到。而由图4-23可知,帐篷映射由上行与下行的两段斜线构成,于是可以用作图的方法由存活1得到存活2。以存活1的点集作纵坐标,存活2的点为横坐标,则存活2的点集可以由帐篷映射的两段斜线作镜像反射从存活1的点来获得。推而广之,我们可以从存活2推导出存活3,进而可以从存活n-1推导出存活n。参照康托尔三分点集图4-3,可以将初始康托尔元看成是由存活(0)的点构成的。一次迭代后留下的存活(1)的点构成生成元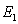 ,二次迭代后留下的存活(2)的点构成生成元
,二次迭代后留下的存活(2)的点构成生成元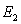 ,如此等等,直至
,如此等等,直至 的点组成康托尔三分集。
的点组成康托尔三分集。
根据康托尔维数计算公式(4-1-5),得斜率为b的帐篷映射奇怪排斥子的维数为:
由式(4-5-8)与(4-5-9),得逃逸速率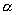 为
为
再注意到李雅普诺夫指数表达式(2-4-6),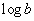 乃是帐篷映射奇怪排斥子的李雅普诺夫指数
乃是帐篷映射奇怪排斥子的李雅普诺夫指数 ,于是逃逸速率
,于是逃逸速率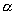 可表示为:
可表示为:

图4-23 帐篷映射中存活1与存活2间的变换
3.魔鬼楼梯的分形维数
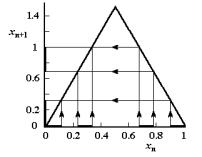
魔鬼楼梯已在第三章第三节中介绍过。它每一个台阶表示两个相互作用系统的锁频关系,一个系统的频率锁定在另一个系统的频率上,锁定的频率大约等于两个系统的有理数频率之比。由于在两个有理数之间还存在无穷多个有理数,所以在两个台阶之间还有无穷多个台阶,参看图3-17,因此魔鬼楼梯具有局部与整体相似的自相似结构,是一个分形图形。
为了确定魔鬼楼梯的分形维数,我们从魔鬼楼梯上挑选出两个相邻的台阶 和
和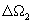 ,如图 4-24所示。它们相应于有理数频率比为
,如图 4-24所示。它们相应于有理数频率比为 和
和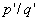 。把两个台阶
。把两个台阶 和
和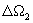 之间的间隔记为
之间的间隔记为 。在两个台阶之间再取一个台阶
。在两个台阶之间再取一个台阶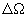 ,它相应的有理数频率比为
,它相应的有理数频率比为 :
:
在图4-24中,p/q=1/5,p'/q'=3/5,所以(p+p')/(q+q')=2/5。有了台阶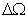 ,就会在区间(
,就会在区间(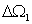 ,
, )和(
)和(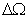 ,
,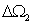 )内出现更小的间隔
)内出现更小的间隔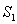 和
和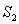 。而这种过程又可以进一步进行下去,以至出现N个(N→∞)间隔
。而这种过程又可以进一步进行下去,以至出现N个(N→∞)间隔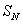 。这样,魔鬼楼梯的分形维数d可由下式确定:
。这样,魔鬼楼梯的分形维数d可由下式确定:
经过数值计算,可求得:
d=0.868±0.002

图 4-24 魔鬼楼梯的分形维数的确定
4. 吸引域边界上的分形
如上所述,耗散系统具有吸引子。如果一个耗散的非线系统存在多个吸引子,则整个相空间就划分为若干个吸引域,它们是“流域”或“盆地”。每个吸引子都有属于自己的吸引域。各吸引域间的边界是代表点流向的“分水岭”。系统在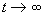 时所呈现的行为依赖于初始点所在的流域。在分水岭上,两个靠得很近但分属于不同流域的代表点,它们会失之毫厘,差之千里,分别流向各自的吸引子。如果初始点是属于同一流域中的点,则会殊途同归,它们都到达同一个吸引子。
时所呈现的行为依赖于初始点所在的流域。在分水岭上,两个靠得很近但分属于不同流域的代表点,它们会失之毫厘,差之千里,分别流向各自的吸引子。如果初始点是属于同一流域中的点,则会殊途同归,它们都到达同一个吸引子。
然而,吸引域的边界有‘光滑’与‘毛糙’之分。如果吸引域的边界是一条光滑的脊梁线,清清楚楚,脊梁线两侧的代表点有各自的流向。诸平庸吸引子流域间的边界,往往就是这样的光滑脊梁线。但是如果系统有若干个奇怪吸引子,它们间的边界却往往是毛糙的,因此也就可能具有复杂的分形结构。这样的吸引域边界处的代表点究竟流向哪一个吸引子,往往具有很复杂的行为。
作为例子,我们讨论来驱动单摆吸引域。驱动单摆的方程由式(3-3-11)表示:
式中q为单摆的品质因子,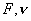 分别为驱动力振幅与频率,
分别为驱动力振幅与频率, 驱动相位。q,
驱动相位。q,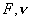 为驱动单摆的三个控制参数。
为驱动单摆的三个控制参数。 为未驱动单摆,它的相图在第一章里就已讨论过,如图4-25a所示。具体图形与品质因子q有关,图4-25a的图形是q=2时的情况。在这个扩展相图上在 [
为未驱动单摆,它的相图在第一章里就已讨论过,如图4-25a所示。具体图形与品质因子q有关,图4-25a的图形是q=2时的情况。在这个扩展相图上在 [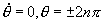 ],
], 等处是吸引子,其中打阴影线的区域是吸引子坐标在原点
等处是吸引子,其中打阴影线的区域是吸引子坐标在原点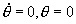 的吸引域。在两个吸引子之间,即在 [
的吸引域。在两个吸引子之间,即在 [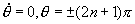 ] 处是单摆的鞍点。有两条
] 处是单摆的鞍点。有两条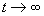 时通过鞍点的流线是单摆的稳定流形,它们是吸引子吸引域的分界线。有两条
时通过鞍点的流线是单摆的稳定流形,它们是吸引子吸引域的分界线。有两条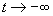 时通过鞍点的流线是发自吸引子的螺旋形曲线,是单摆的不稳定流形。
时通过鞍点的流线是发自吸引子的螺旋形曲线,是单摆的不稳定流形。

图 4-25 未驱动单摆的吸引子与吸引域
当驱动力存在时,平面相图变成三维的空间相图(参见图1-28),新加进的坐标是驱动力相位 ,每个
,每个 (mod
(mod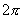 )的平面是庞加莱截面。系统的动力学行为要用庞加莱截面来研究,本节均取
)的平面是庞加莱截面。系统的动力学行为要用庞加莱截面来研究,本节均取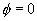 的庞加莱截面。如前所述,当周期轨道的周期等于驱动力的周期时,在庞加莱截面上是一个不动点。
的庞加莱截面。如前所述,当周期轨道的周期等于驱动力的周期时,在庞加莱截面上是一个不动点。
现在假设驱动力的幅度很小,单摆的摆角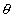 远小于
远小于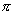 ,此时单摆吸引子的庞加莱截面和它的吸引域与图4-25非常相象。在与每个吸引子相对应的势阱(参见图1-10)中,运动仍然是周期的吸引轨道,其周期为
,此时单摆吸引子的庞加莱截面和它的吸引域与图4-25非常相象。在与每个吸引子相对应的势阱(参见图1-10)中,运动仍然是周期的吸引轨道,其周期为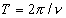 。在庞加莱截面上吸引子仍然是单点,分割各个吸引子的吸引域的边界乃是光滑曲线。
。在庞加莱截面上吸引子仍然是单点,分割各个吸引子的吸引域的边界乃是光滑曲线。
当加大驱动幅度,单摆的摆角 接近于
接近于 甚至超过
甚至超过 时,则系统将产生对称性破缺(参见第一章第二节)。对称破缺使原来 [
时,则系统将产生对称性破缺(参见第一章第二节)。对称破缺使原来 [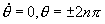 ]吸引子变为不稳定点,并产生与变换
]吸引子变为不稳定点,并产生与变换 ,
,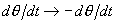 ,
,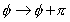 相关的新吸引子对。与原来吸引子不同,新产生的吸引子其平均角速度不为零,而是
相关的新吸引子对。与原来吸引子不同,新产生的吸引子其平均角速度不为零,而是 ,这里m,n为非零的整数。平均角速度
,这里m,n为非零的整数。平均角速度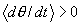 的吸引子的吸引域与
的吸引子的吸引域与 的吸引子的吸引域的边界将具有分形特征。
的吸引子的吸引域的边界将具有分形特征。
选取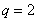 ,驱动力相位
,驱动力相位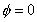 ,频率
,频率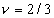 ,对三个驱动力振幅
,对三个驱动力振幅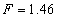 ,1.48,1.954,则都将出现由对称破缺产生的吸引子对。与这三个驱动力相对应的相图如图4-26 (a)到(c)所示。在作图时,对于平均角速度
,1.48,1.954,则都将出现由对称破缺产生的吸引子对。与这三个驱动力相对应的相图如图4-26 (a)到(c)所示。在作图时,对于平均角速度 的吸引子的吸引域用黑色表示,对于平均角速度
的吸引子的吸引域用黑色表示,对于平均角速度 的吸引子的吸引域用白色表示。吸引域的作图区间是
的吸引子的吸引域用白色表示。吸引域的作图区间是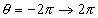 以显示其周期结构,吸引子的庞加莱截面的区间是
以显示其周期结构,吸引子的庞加莱截面的区间是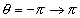 。
。
图(a)为 情况,吸引子是一对周期4轨道,它们的平均角速度分别为
情况,吸引子是一对周期4轨道,它们的平均角速度分别为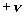 与
与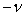 。对于
。对于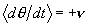 的周期4吸引子,有两点位于
的周期4吸引子,有两点位于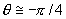 ,
, 附近,另外两点在
附近,另外两点在 ,
,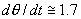 附近,它们分别是图上两个白色斑点中的两个小黑点;对于
附近,它们分别是图上两个白色斑点中的两个小黑点;对于 的周期4吸引子,有两点的坐标
的周期4吸引子,有两点的坐标 ,
,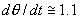 附近,另外两点的坐标在
附近,另外两点的坐标在 ,
, 附近。从大范围结构上来看,这些周期吸引子的吸引域与未驱动单摆的相图图4-25相类似,但是从小尺度上看,不同吸引子的吸引域有一个狭窄的混合区域,从而将较大的、连续区域割裂开来。
附近。从大范围结构上来看,这些周期吸引子的吸引域与未驱动单摆的相图图4-25相类似,但是从小尺度上看,不同吸引子的吸引域有一个狭窄的混合区域,从而将较大的、连续区域割裂开来。

图 4-26 驱动单摆的吸引子与吸引域
图4-26(b)和(c)分别是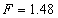 与
与 时的情况,这里混沌吸引子对的吸引域。在图(b)中,
时的情况,这里混沌吸引子对的吸引域。在图(b)中, ,每个吸引子的两个带落在与上面的周期吸引子的一对点的相同位置附近,并与它们的平均角速度相同。在图(c)中,
,每个吸引子的两个带落在与上面的周期吸引子的一对点的相同位置附近,并与它们的平均角速度相同。在图(c)中,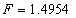 ,混沌吸引子的平均角速度分别为
,混沌吸引子的平均角速度分别为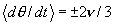 ,其中
,其中 的混沌吸引子的三个带位于:
的混沌吸引子的三个带位于:
而角速度为 的混沌吸引子的三个带位于:
的混沌吸引子的三个带位于:
综观图(a)到图(c)可以发现,总体上三个图吸引域的结构是相似的,但吸引域的最大宽度随F的增加而减小,混合程度随F的增加而增加。吸引域的边界都是由与吸引子平均角速度相同的一对鞍轨线的稳定流形所构成的分形集。如果沿吸引子的吸引域的对角线切割以下,可以见到吸引域的是一康托尔点集。这样的结构分形维数可用本章第三节所讲的关联函数进行计算。计算表明,与三个驱动幅度 ,1.48,1.954相对应的维数为1.63,1.88和1.97。
,1.48,1.954相对应的维数为1.63,1.88和1.97。
5. 一维映射的分形分析
由上述讨论可见,至少要有两个李雅普诺夫维数才能利用式(4-5-16)计算一个奇怪吸引子的维数,因此该式不适用于只有一个李雅普诺夫指数的一维映射。一个一维映射如果它的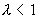 ,则
,则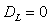 ;如果
;如果 ,则
,则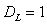 。为了具体地理解这个结论,我们看一下一维平方映射:
。为了具体地理解这个结论,我们看一下一维平方映射:
我们知道它有一个临界参数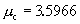 。当
。当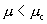 时,平方映射收敛到不动点或倍周期分岔,倍周期分岔一直持续到临界点mc时终止,相应的李雅普诺夫指数λ是负的,
时,平方映射收敛到不动点或倍周期分岔,倍周期分岔一直持续到临界点mc时终止,相应的李雅普诺夫指数λ是负的,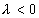 。如果我们用一根线段上的点来表示倍周期分岔的分岔点,那么随着
。如果我们用一根线段上的点来表示倍周期分岔的分岔点,那么随着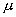 值接近
值接近 ,倍周期分岔次数越来越多,线段上的点会越来越密,然而它们都是分离的点,因此其维数仍为0。
,倍周期分岔次数越来越多,线段上的点会越来越密,然而它们都是分离的点,因此其维数仍为0。
再看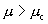 的非周期情况。由于非周期性,迭代没有终结,迭代点始终在线段上迂回徘还,密密地布满了[0,1]的整个区域,它的维数应为1。所以与非周期性的混沌运动相应的李雅普诺夫指数
的非周期情况。由于非周期性,迭代没有终结,迭代点始终在线段上迂回徘还,密密地布满了[0,1]的整个区域,它的维数应为1。所以与非周期性的混沌运动相应的李雅普诺夫指数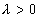 ,相应的维数为1。
,相应的维数为1。
那么在一维映射中是否还有分数维呢?如果有,唯一可能的区域是 附近。回忆图2-27的平方映射的李雅普诺夫指数随
附近。回忆图2-27的平方映射的李雅普诺夫指数随 值的变化曲线,可看出
值的变化曲线,可看出 有三种情况:一是
有三种情况:一是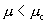 时各个分岔点
时各个分岔点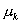 ,k=1,2,3…;二是混沌区域中的周期窗口起点的切分岔处;三是临界点
,k=1,2,3…;二是混沌区域中的周期窗口起点的切分岔处;三是临界点 及混沌区中周期窗口结束处。
及混沌区中周期窗口结束处。
先看各个分岔点 ,这里指数
,这里指数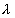 值由负接近于零,再返回到负值。实际上,当迭代趋近于各个分岔点是一个越来越慢的结网过程,图4-27是
值由负接近于零,再返回到负值。实际上,当迭代趋近于各个分岔点是一个越来越慢的结网过程,图4-27是 接近于3时平方映射趋近于不动点的迭代图,可见越接近不动点,迭代速度越来越慢,在映射迭代中被称为慢化现象。这种迭代的慢化现象也出现在各个其他的分岔点处,从而造成了分形图象。
接近于3时平方映射趋近于不动点的迭代图,可见越接近不动点,迭代速度越来越慢,在映射迭代中被称为慢化现象。这种迭代的慢化现象也出现在各个其他的分岔点处,从而造成了分形图象。

图4-27 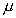 接近于
接近于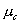 时平方映射趋近不动点的迭代过程
时平方映射趋近不动点的迭代过程
为简单起见,分析不动点附近的情况。首先的目的是求得不动点附近因迭代慢化造成的点分布。为此目的把坐标原点移到不动点处,平方映射得迭代关系可以写为:
式中a为展开系数,忽略 以上的高阶项,二次迭代关系为:
以上的高阶项,二次迭代关系为:
于是有
定义迭代点的分布密度 ,由式(4-5-14)得:
,由式(4-5-14)得:
 (4-5-15)
(4-5-15)
需要注意,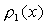 描述的是迭代过程中的点分布,它是迭代的暂态过程,与[0,1]线段上的倍周期分岔点位置的分布不同。
描述的是迭代过程中的点分布,它是迭代的暂态过程,与[0,1]线段上的倍周期分岔点位置的分布不同。
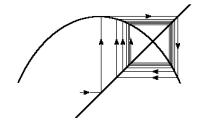
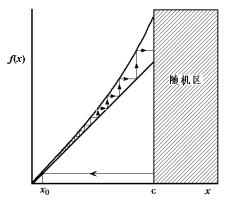
现在采用计算容量维数的方法计算不动点区的维数,于是可用一长度为e 的线段来覆盖,这是一个用点分布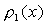 描述的非常狭窄的区域。由式(4-5-15)或图4-27可见,点分布
描述的非常狭窄的区域。由式(4-5-15)或图4-27可见,点分布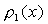 的特点是随x从高度密集到非常稀疏单调地变化的,因此可以找到某个
的特点是随x从高度密集到非常稀疏单调地变化的,因此可以找到某个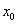 ,在
,在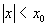 时,每段
时,每段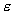 都能覆盖到x上的点,而在
都能覆盖到x上的点,而在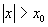 时,许多段才能覆盖到一个点。考虑
时,许多段才能覆盖到一个点。考虑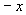 与
与 ,全部范围内的总点数为:
,全部范围内的总点数为:
将式(4-5-15)代入(4-5-16),通过积分得:
由式(4-2-3),最终求得容量维数是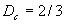 。对于其他各个分岔点
。对于其他各个分岔点 的分维也可以与此同样的方法进行计算。
的分维也可以与此同样的方法进行计算。
其次讨论混沌区域中周期窗口起点的切分岔处的分形。这里指数 由正值经零进入到负值。根据第三章阵发性混沌的讨论,切分岔处的迭代关系为
由正值经零进入到负值。根据第三章阵发性混沌的讨论,切分岔处的迭代关系为
即有:
于是得切分岔处的点分布 :
:
与式(4-5-16)类似,求得切分岔处的总点数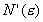
将式(4-5-18)代入(4-5-17),通过积分得:
于是求得切分岔处的容量维数是 。
。
最后,关于临界点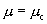 附近及混沌区中周期窗口结束处的分形维数。这里
附近及混沌区中周期窗口结束处的分形维数。这里 值由负越过
值由负越过 转为正值,系统从规则运动进入混沌状态。这里的分形维数计算起来比较复杂,需要用到多重分形及重正化理论,这里不作进一步的介绍,文献所报道的数值为
转为正值,系统从规则运动进入混沌状态。这里的分形维数计算起来比较复杂,需要用到多重分形及重正化理论,这里不作进一步的介绍,文献所报道的数值为
D=0.538┄
6.  噪声 时序中的自相似性
噪声 时序中的自相似性
前面我们分析的各种分形对象,无论是象康托尔集等那样规则分形,还是象布朗运动那样的无规分形,它们都是在空间上自相似的。类似地,对于时间信号也可以存在一定的自相似,称为时序中的自相似性。
从电信号的角度讲,时序信号无非是按一定时间间隔取值的电流或电压信号,其中包括相伴的噪声。从事电子测量的人都知道,噪声总是与测量信号同时存在的。噪声是一种随机起伏,在任何时刻,它的幅度、波形及相位都是随机的。根据功率谱的不同特性,噪声还可以分成不同的类型。有一些噪声,它们的功率谱与频率f无关,常称白噪声,例如由导体内电子随机运动引起的热噪声就属于白噪声。然而有一种低频噪声,其强度是随频率的降低而增加的,它们的功率谱密度为:
式中K为比例系数,指数a在不同的测量场合取不同的数值,约在0.8~1.4之间,常称为 噪声。
噪声。 噪声虽然发现很早,但是它的产生的机理至今仍不很清楚,一般认为它与电子元器件的制造工艺有关。
噪声虽然发现很早,但是它的产生的机理至今仍不很清楚,一般认为它与电子元器件的制造工艺有关。
令人惊异的是在大自然,社会经济,以及人们生活等各种各样场合,类似于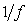 噪声的现象随处可见。美妙的音乐,城市公共交通的密度,大江大河的水位,人类心率的跳动,股市的变化等等都在一定程度上存在类似于
噪声的现象随处可见。美妙的音乐,城市公共交通的密度,大江大河的水位,人类心率的跳动,股市的变化等等都在一定程度上存在类似于 噪声。由此可以想见,
噪声。由此可以想见, 噪声的产生是一种随机过程,但具体的机制不可能只有一种,应是多种多样的。作为例子,这里介绍一个能产生
噪声的产生是一种随机过程,但具体的机制不可能只有一种,应是多种多样的。作为例子,这里介绍一个能产生 噪声的映射:
噪声的映射:
这个映射的特点是,如果初始值 很小,接近于零,则映射
很小,接近于零,则映射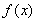 的增长是很缓慢的,开始一段总是保持一个很小的数值,但当
的增长是很缓慢的,开始一段总是保持一个很小的数值,但当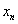 增长到某个程度时,
增长到某个程度时,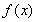 增长加快,以至于表现出一种“突变”行为,如图4-28所示。有意思的是
增长加快,以至于表现出一种“突变”行为,如图4-28所示。有意思的是 在作数次大幅度的跳跃以后,会重新进入到零值附近。此后
在作数次大幅度的跳跃以后,会重新进入到零值附近。此后 又重复出现上述过程,开始缓慢增长,然后作大幅度的跳跃。显然,初始阶段慢增长的持续时间与x接近于零的程度密切相关,因此发展成大幅度的跳跃也是变化多端的。实际上,这就是前面讨论过的非线性系统进入到了阵发性混沌状态。
又重复出现上述过程,开始缓慢增长,然后作大幅度的跳跃。显然,初始阶段慢增长的持续时间与x接近于零的程度密切相关,因此发展成大幅度的跳跃也是变化多端的。实际上,这就是前面讨论过的非线性系统进入到了阵发性混沌状态。

图4-28 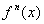 开始缓慢增长,然后作大幅度的跳跃
开始缓慢增长,然后作大幅度的跳跃

图4-29 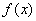 无规脉冲序列
无规脉冲序列
如果将上述 的变化在时间图上表示,那么
的变化在时间图上表示,那么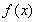 的大幅度的跳变形成的是一种无规脉冲序列,如图4-29A所示。按照傅立叶分析,无规脉冲序列相应着具有非常丰富的频率分量。采用滤波方法,我们可以使其只含无规脉冲中给定的频段分量。例如,图4-29B、C和D分别给出了只含频段1.5到15Hz,15到150Hz,150到1500Hz成分的波形图。于是我们看到,这三个滤波出的信号虽然出现在非常不同的时间标度上,但是它们是相似的,因此也是一种分形结构。
的大幅度的跳变形成的是一种无规脉冲序列,如图4-29A所示。按照傅立叶分析,无规脉冲序列相应着具有非常丰富的频率分量。采用滤波方法,我们可以使其只含无规脉冲中给定的频段分量。例如,图4-29B、C和D分别给出了只含频段1.5到15Hz,15到150Hz,150到1500Hz成分的波形图。于是我们看到,这三个滤波出的信号虽然出现在非常不同的时间标度上,但是它们是相似的,因此也是一种分形结构。
7.复数域上的分形
如上所述,一维动力学方程(4-5-5)的帐篷映射,它可产生复杂的分形边界。然而用一个二维方程可以产生的产生更复杂、更美丽花样的分形边界。我们从熟知的平方映射出发:
定义一个新变量: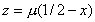 ,即
,即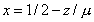 ,将其代入上式后得新的映射:
,将其代入上式后得新的映射:
式中
我们注意到方程(4-5-21)有两个根:
是该映射的两个不动点。由
可以确定解(4-5-22)的稳定性。可见,任何满足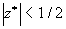 的不动点,这时的
的不动点,这时的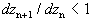 ,所以这些不动点都是稳定的。
,所以这些不动点都是稳定的。
然而我们事先还没有设定式(4-5-21)中的c值。实际上对于不同参数c,解(4-5-22)的稳定性还有非常复杂的行为。将稳定性条件应用于式(4-5-22),通过简单计算可知,当c值满足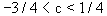 时,不动点是稳定的;而当
时,不动点是稳定的;而当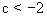 或
或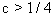 时,则不动点是不稳定的,此时,对式(4-5-21)进行迭代可出现向
时,则不动点是不稳定的,此时,对式(4-5-21)进行迭代可出现向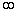 逃逸现象。人们将那些迭代不产生
逃逸现象。人们将那些迭代不产生 逃逸的c值的集合称为曼德布罗特集。
逃逸的c值的集合称为曼德布罗特集。
其次,注意到参数c出现在式(4-5-22)中的方根号内,因此,对于某些参数c值,式(4-5-22)的不动点是复数,例如设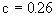 时,则
时,则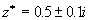 ,
,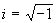 ,不动点就是复数。然而,如果初始值
,不动点就是复数。然而,如果初始值 为一个纯实数,则所有迭代得到的
为一个纯实数,则所有迭代得到的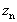 数也都是实数,所以不会出现不动点为复数的情况。实际上当c为纯实数时,方程(4-5-21)仅相当于平方映射,迭代不会出现任何异常情形。只有当
数也都是实数,所以不会出现不动点为复数的情况。实际上当c为纯实数时,方程(4-5-21)仅相当于平方映射,迭代不会出现任何异常情形。只有当 为复数时,迭代才可能产生复数
为复数时,迭代才可能产生复数 。因此如果允许我们取c为复数,方程(4-5-21)将展现出复数不动点的动力学行为。
。因此如果允许我们取c为复数,方程(4-5-21)将展现出复数不动点的动力学行为。
我们注意一下复数不动点动力学行为。若以 为初始条件出发,取以复数c值为变数进行迭代计算,并在迭代计算中注意向
为初始条件出发,取以复数c值为变数进行迭代计算,并在迭代计算中注意向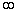 逃逸的情况。迭代是在复平面上进行的,每个c值是复平面上的一个点。图形对所取c值展开,作图时规定,若迭代产生
逃逸的情况。迭代是在复平面上进行的,每个c值是复平面上的一个点。图形对所取c值展开,作图时规定,若迭代产生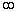 逃逸,则将这个c点涂以黑色,如不产生逃逸,则该点保留为白色。采用如此方法,我们可以作出一幅结构非常复杂的图形来,这便是曼德布罗特集花样的图形,如图4-30所示。
逃逸,则将这个c点涂以黑色,如不产生逃逸,则该点保留为白色。采用如此方法,我们可以作出一幅结构非常复杂的图形来,这便是曼德布罗特集花样的图形,如图4-30所示。
图4-30a为参数c取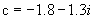 到
到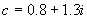 时获得的图,这是一个整体的曼德布罗特集图形。图4-31b与图4-31c分别为图a中用箭头b与c指向的小区域的高分辨图,图4-30d为图4-30c中一根须线进一步分辨后的图形。由这些图可见,当分辨越来越更精细时,则图中各个细节就越来越明显地显示出来。这是一张处处是分形的奇妙无比的图形。读者可以用这里提供的程序,对所感兴趣的参数c范围进行运算与作图。
时获得的图,这是一个整体的曼德布罗特集图形。图4-31b与图4-31c分别为图a中用箭头b与c指向的小区域的高分辨图,图4-30d为图4-30c中一根须线进一步分辨后的图形。由这些图可见,当分辨越来越更精细时,则图中各个细节就越来越明显地显示出来。这是一张处处是分形的奇妙无比的图形。读者可以用这里提供的程序,对所感兴趣的参数c范围进行运算与作图。


a b


c d
图4-30 以c实数为横轴,虚数为纵轴平面上的曼德布罗特集
曼德布罗特集的Qbasic计算程序如下:
SCREEN 12
VIEW (0, 0)-(630, 470), 15, 2
WINDOW (0, 0)-(630, 470)
x = -2.1: y = -1.3
l = .01
n = m = 0
WHILE x <= .8
IF INKEY$ = "x" GOTO f
WHILE y < 1.3
a = 0: b = 0
IF INKEY$ = "x" GOTO f
FOR i = 1 TO 30
IF INKEY$ = "x" GOTO f
c = a ^ 2 - b ^ 2 + x
d = 2 * a * b + y
IF SQR(c ^ 2 + d ^ 2) > 50 THEN
PSET (l * m * 100 + 100, l * n * 100 + 100), 0
GOTO f1
END IF
a = c: b = d
NEXT
PSET (l * m * 100 + 100, l * n * 100 + 100), 15
f1: y = y + l
n = n + 1
WEND
x = x + l
m = m + 1
y = -1.5
n = 0
WEND
f: END
主要参考文献
1.R.Z.Sagdeev, Nonlinear physics Harword Academic Publishers, London,1988
2.D.Kaplan, L.Glass, Understanding Nonlinear Dynamics, Springer-Verlag, 1995
3.B.曼德尔布洛特,分形对象—形、机遇与维数,世界图书出版公司,1999
4.肯尼思.法尔科内,分形几何—数学基础与应用,东北工业学院出版社,1991
5.董连科,分形理论及应用,辽宁科学技术出版社,1991
6.郝柏林,从抛物线谈起—混沌动力学引论,上海科技教育出版社,1993
7. E.G. Gwinn, R.M. Westervelt, Fractal basin boundaries and intermittency in the driven damped pendulum, Physical Review A, 33 (1986) 4313
8.J.C.Sprott, Theching Notes,http//sprot.physics.wisc.edu
No comments:
Post a Comment