|||
7. 能级和能带(二)
从上次的叙述,我们知道,在固体中,单原子电子的一个能级,分裂而成了多原子的多个共有电子所可能占据的一条能带。能带中包含了N个靠得很近的分离能级。这个N所代表的是固体中的原子数,是个非常大的数字。例如,在每一立方厘米的硅材料中,含有5*1022个硅原子。因此,可以将一条能带看成是包含了无穷多个连续的能级。所以,在图2和图3中,能带便被表示成涂了颜色的一片连续区域。
但是,通常我们看到的能带图,并不是一片连续区域,而是一条一条的曲线。比如说,图4(a)所显示的,便是硅的部分能带图。图中数条曲线龙飞凤舞,并没有如图3中的那种连续区,这又是怎么回事呢?
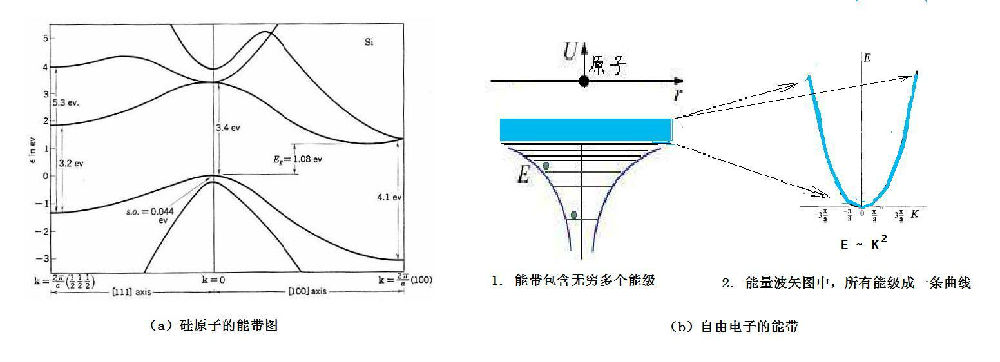
图4
这其中最主要的奥秘,是因为我们在图3中,只画出了能级的高低,忽略了电子运动时的另一个特征:动量。而电子的能量和动量是相关的。这点概念在经典力学中就很清楚,如果考虑相对论力学,也有相应的能量动量关系,只不过公式略有不同而已。在量子力学中,电子的运动用波函数描述,能量动量关系便被能量与波矢之关系所代替。
比如,我们研究脱离了原子束缚的自由电子(图4b)。自由电子的能量E,与其波矢k的平方成正比,如果将自由电子的每个能级所对应的波矢大小也考虑进去,将波矢作为横轴的话,图4b1中的淡蓝色连续区域,就演变成了图4b2中的淡蓝色连续曲线。
用个通俗的比喻来说明这个问题。图4b1中的连续区域中,用一条水平线表示某个电子占据了这层楼,而实际上的电子只住在这层楼的一个房间,电子所占楼层的高度还与房间离中心的距离有关,图4b2便描述了楼层高度与此距离之关系。
现在再回过头来看图4(a),就比较明白了,那些一条一条的曲线,原来是表示在波矢空间中,硅原子电子的不同能带!不过,仍然有读者会心存疑惑:你这儿所谓的‘波矢空间’是什么意思啊?
能带论应用的最重要领域是固体,大多数固体是原子整齐排列的晶体。为理解波矢空间,让我们再多介绍一点固体物理的基本知识。
在固体中所谓的自由电子,并不是绝对‘自由’的。每个自由电子都是在所有的晶格离子的势场以及其它所有电子的平均势场中运动。晶体中的离子形成各种规则的、周期性的排列。这种规则性和对称性,因各种材料的不同而不同。比如说,硅晶体的结构是一种面心立方结构。简单地说,面心立方晶格就是由一个一个的立方体组成,除了在立方体的顶点上各有一个硅原子(离子)之外,在6个面的中心处还各有一个硅原子,见图5(a)。硅晶体中的自由电子就在这种原子排列构成的周期势场中运动。

图5
很有趣。看看与晶体研究有关的几位物理学家,名字翻译成中文之后都是姓‘布’的。比如说,大家可能听过:布拉菲晶格、布拉格反射、布洛赫波、布里渊区。罗列一遍这几个‘布’先生对固体物理的贡献,对晶体能带的知识也就略知一二了。
第一位布先生是200多年前出生的法国物理学家奥古斯特·布拉菲(AugusteBravais,1811年-1863年)。尽管早在16世纪后期,人们就对晶体外在表现的规则形状有了初浅的认识,但直到有了原子模型之后,科学家们才开始根据晶体的外部形状,揣摩它们的内部结构,试图给出原子在物体中规则排列的各种可能性。正是这位布拉菲先生,首次将群的概念应用到物理学,于1845年得出了三维晶体原子排列的7大晶系和所有14种可能存在的点阵结构,为固体物理学做出了奠基性的贡献【1】。
布拉菲建立了三维晶体的14种点阵模型,但是,到底哪种物质晶体具有哪种点阵呢?这还得用实验一个一个地进行确定。也就是说,最好是有某种方法,打进晶体内部去‘看一看’。‘看’东西的最好手段不就是使用各种颜色的光吗,但是,普通的光对探索晶体好像无能为力。那时候,科学家们刚刚结识了一位陌生的女士,人们把它叫做‘X-ray’,或称之为‘伦琴射线’。德国科学家威廉·伦琴(Wilhelm Röntgen,1845年-1923年),就因为苦苦追求这位‘才女’而捧走了瑞典国王第一次颁发的诺贝尔物理奖。尽管伦琴很谦虚、很低调,尽管他全部捐出了诺贝尔奖金,放弃了发现X射线的专利权,也坚决反对用他的名字命名此位‘女士’,但人们经常还是固执地称X-ray为伦琴射线,以纪念这位伟大的学者。
伦琴射线确实是才高艺广,能干很多可见光干不了的事情。诸如穿透人体显示骨骼之类的事情,她干起来得心应手,令人称羡。当时的物理学家们猜测,伦琴射线其实就是与可见光本质相同的电磁波,只不过波长更短得多而已。但如何证明这点呢?要证明波动性的最好方法就是让它产生干涉或衍射图案,像可见光经过光栅时产生衍射那样。但人们做不出这种光栅,因为尺寸太小了!光栅只对与其尺寸大小相仿的波动表现出衍射现象。这也和显微镜分辨率的概念一样:要想看清物体,必须使用波长小于或等于物体尺寸大小的光。而要观察波长范围在0.01纳米到10纳米之间的伦琴射线的波动性,需要用原子尺度的光栅!
科学家又想,晶体结构不就是一种原子尺度的光栅吗?最早做这件事情的是德国物理学家马克思·冯·劳厄(Max von Laue,1879年—1960年),他因此而得了1914年的诺贝尔物理奖。后来,这个领域又加入了两位‘布’先生,还是父子兵共同上阵,他们是亨利•布拉格(Sir WilliamHenry Bragg, 1862-1942)和他的儿子劳伦斯•布拉格(Sir William Lawrence Bragg,1890--1971)。最后,这布拉格父子分享了1915年的、原来传说要颁给特斯拉的诺贝尔物理奖,这是唯一一次父子同上诺贝尔讲台领奖,被传为佳话,并且,小布拉格当时只有25岁,是迄今为止最年轻的诺贝尔奖得主。
布拉格父子所做的诺奖级贡献,其实看起来很简单。如果说劳厄的工作证实了x射线是一种电磁波,布拉格父子则是用这种电磁波,开创了x射线晶体结构分析学,为后人用x射线,以及电子波、中子波等,研究晶体结构,建立了理论基础。图6(a)是布拉格反射定律的示意图,由图可见,对某个入射角θ,如果从两个距离为d的平行晶面反射的两束波之间的光程差,正好等于波长λ的整数倍时,便符合两束波互相干涉而加强的条件:2d sinθ = nλ,另外一些角度,则可能符合两束波互相干涉而相消的条件,这样,我们就能在接受屏上观察到衍射图像。
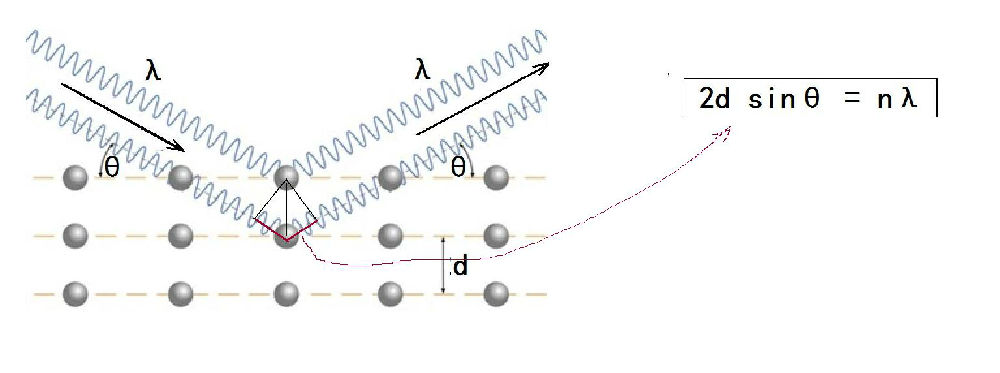
图6
No comments:
Post a Comment