無論溫度降至多低，電子依然會因為動量的不確定而以海森堡速度運動，並貢獻出壓力
Everett on 海森堡速度, 电子简并压力
1.3节讲的是量子场论中的无穷大问题。
两个“无穷大”的例子
P31讲的是电子自能的无穷大问题。没有查阅相关文献，因而我对具体细节不是很了解。总而言之，是通过二阶微扰论的方法计算电子自能的。涉及到的过程似乎是这样的：能量为
的电子，放出一个动量
的光子后能量变成
，随后又吸收了这个光子，所以末能量仍旧是。这样计算出来的电子自能，随着光子动量的增加，是呈对数发散的。P32，“An infinity of...”开始讲的是真空极化，Dirac的模型是负能级上填满了电子，正能级上，有一定的电荷密度。负能级上填满电子，即是我们所说的“真空”；正能级上的电荷则是我们所观察到的电荷。电荷和真空相互作用，产生真空极化现象，从而改变我们观察到的电荷密度，其值如Eq. (1.3.3)所示，其中的
是对数发散的。修补量子场论
P33上长长的一段讲了几种人们想到的解决无穷大问题的方案。当时的人们普遍认为，是量子场论理论本身的问题导致了无穷大的出现，因此解决问题，就必须对理论进行修改。
Heisenberg的方案是最直接的。避免发散的最直接方法是做截断，Heisenberg假设存在基本长度
，量子场论只在大于这个基本长度的尺度上成立。有人猜想量子场论应有non-local的结构，因此建议场论的形式应由态矢、场算符的描述改为仅由可观察量（例如S矩阵）所作的描述。
Wheeler和Feynman在研究电磁场时发现，计算推迟势时，除了考虑源和试探电荷，还应把宇宙中所有电荷都考虑在内。
Dirac则假设存在一些负几率的态（an 'indefinite metric' in Hilbert space），在对所有态求和时，这些态可以消除无穷大。
重整化
相比于上面的方案，重整化是一个“more conservative idea”。Perhaps these infinities could all be absorbed into a redefinition, a 'renormalization' of the parameters of the theory. 重整化要求改变的是我们对理论的认识，而非量子场论理论本身。
例子：我们认为电子的裸电荷是无穷大，（即对电子电荷做了redefinition）。而真空极化导致我们观察到的电荷和电子的裸电荷不同，其修正是Eq. (1.3.3)，也有一个无穷大。两个无穷大抵消，于是我们观察到的电荷（物理电荷）是有限的。
量子电动力学将电磁场量子化，建立起来的方程能说明电磁波是由光子组成的
重正化1http://www.physixfan.com/
宇宙间时空分辨率的极限——普朗克长度和普朗克时间
作者： physixfan /*在《套套神教圣经·创世纪》里，我提到了空间最小单元普朗克长度和时间最小单元普朗克时间的说法，估计很多人不知道这是什么意思，故写此文来科普一下。本文不需要学过量子场论等高端课程就可以阅读 只要不求甚解即可...*/
我要是说，在我们真实生活的宇宙里，时空其实是分立的而不是连续的，也许很多人会感到很惊异觉得这是一种科幻。但是一部分激进的理论物理学家的确是这么认为的，我也很认同这种观点。分立的时空格子的尺度，被称作普朗克长度和普朗克时间。首先给出它们的表达式和大小吧：
普朗克长度：ℓ P =ℏGc 3 − − − √ ≈1.616199(97)×10 −35 m
普朗克时间：t P =ℏGc 5 − − − √ ≈5.39106(32)×10 −44 s
其中ℏ 是普朗克常数，c是光速，G是万有引力常数。没错，普朗克长度和普朗克时间的表达式，正是由宇宙间最基本的三个常数组合而成的具有长度、时间量纲的物理量。高中时候就见过这个看起来很神奇的表达式，不过一直不知道其物理含义到底是什么，为什么就可以代表时空的最小分辨率。直到今年上的量子场论和物理宇宙学两门课让我略懂了其物理内涵。
首先要知道的是，目前描述我们这个宇宙的最基本最底层的理论之一是量子场论，而我们有很充分的理由相信，量子场论里存在一个物理的能量截断，即量子场论只有在能量低于这个截断能量的时候才有意义。这一段后半部分的内容直接摘抄自刘川的量子场论讲义：对于一个有相互作用的量子场论来说，由于量子涨落的“虚过程”可以在任意能动量发生，因此，如果理论不存在某种能动量截断，那么由于长是互相作用的，一个低能动量的模式就可以通过虚过程与无穷高能动量的模式发生相互作用，这就造成了场论中的“紫外发散”（即计算得到的结果是无穷大）。而如果量子场论中存在一个物理的能动量截断，它就可以保证所有的量都不发散。这个截断的具体形式其实对于远低于截断能标的物理来说并不重要，因为低能区的物理对截断的形式并不敏感。重要的是，这个截断是存在的，而且它是相互作用量子场论不可或缺的组成部分。
然后，根据不确定性关系这一量子力学的基本原理，
ΔxΔp≥ℏ
ΔtΔE∼ℏ
能动量存在着一个上截断，就意味着时空存在着一个下截断。即空间存在最小分辨率。
以上从量子场论的角度，分析了这样一个时空最小分辨率的存在性，但是并没有给出它的具体形式。其具体表达式则是由宇宙学中对量子引力极限的估计给出的。
众所周知，如果一个物体的半径相对于其质量小到了一定程度，它就会形成黑洞。形成黑洞所需要的质量和半径的关系由所谓的Schwarzschild半径给出，它是通过解Einstein方程得到的解：r s =2Gmc 2 ，其中G和c仍是万有引力常数和光速，m是质量。当质量为m的物体的半径小于Schwarzschild半径时它就成了一个黑洞。
另一方面，基本的量子力学知识告诉我们一个物体的de Broglie波长为：λ=2πℏp ，其中p为动量。
量子引力极限的估计是这样的：当一个物体的Schwarzschild半径与de Broglie波长相当时，那么对这个物体的研究就必须知道黑洞内部要如何描述，即现有的一切物理理论都失效了，必须使用量子引力论来处理（而自洽的量子引论人类还没有建立起来）。联立Schwarzschild半径与de Broglie波长的表达式让他们相等，再加上质能关系E=mc^2和极端相对论性条件E=pc，就可以解出这个长度究竟是多大了。忽略掉并不改变数量级的常数之后，得到的结果正是：普朗克长度。普朗克时间的计算其实只要由普朗克长度除以c就可以得到。
如此一来，我们就已经清楚普朗克长度和普朗克时间的物理意义了：它确确实实是宇宙时空的最小分辨率，如果想探测比这更小的时空，你所使用的能量会如此之高以至于它自己会形成一个黑洞。
不过其实时空到底是分立的还是连续的，对人类生活一点影响都没有。普朗克长度和普朗克时间实在是太小太小，以至于夸克和电子的尺度都比它要大好几十个数量级呢。
接下来，Max Tegmark详细的讨论了什么叫做Integration(整体性)。在他看来，我们的世界是分层次的客体。比如说，你正在喝一杯冰水，你会感受到在玻 璃杯中有冰块。玻璃和冰块是分立的客体，因为它们都各自是一个整体且相对独立，它们内部的联系远远比与外部的联系紧密。我们可以定义物体的稳定性为集成温 度（把整体分离为部分所需的能量密度）和独立性温度（在层级内把母辈物体分离开所需的能量密度）之比。比如说，冰块的独立温度大概是3毫开，集成温度大概 是300开，稳定性是
。在下一级的结构中，氧原子和氢原子的稳定性都是10。氧原子核的稳定性是。稳定性越高，这个物体越容易被我们感知和定义。
他发现，利用纠错码，经典物理允许信息基本上完全地被集成。任意一个包含至少半个比特的信息的子系统就可从剩下的比特中重建出来。存储在Hopeld neural networks (Hopeld神经网络）中的信息是天然的可纠错的。但是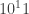
个 神经元只能支持大概37个比特的集成了的信息。这就带来了一个集成化的悖论：为什么在我们意识体验所包含的信息内容似乎远大于37个比特。更糟的是，他发 现把这个结果推广到量子信息领域，反而加重了集成性悖论：量子信息系统只能支持不多于四分之一集成化的比特。实际上，对于任意大的量子系统，无论我们如何 编码，它所包含的可集成的信息都不会超过四分之一个比特。这强烈的暗示我们，集成性原理至少需要一个附加的原理作为补充。
他接下来探讨了独立性原理，讨论了如何通过希尔伯特空间分解实现其对应的哈密顿量分立为互相独立的部分。他发现了量子芝诺效应悖论：如果我们把宇宙分为最 为相互独立的几个客体，那么所有的运动都会陷入中止。既然有意识的的观察者显然没有感受到任何的停滞，那么集成性和独立性原理必须还需要至少一个原理来作 为补充。
进一步的，他研究了动力学原理，因为有意识的系统不仅能存储信息，还要能处理它。他认为能量相干性（energy coherence）
可以作为动力学的合适度量，它与时间无关，且在某些纯态情况下约化为能量的不确定性
。把动力学最大化只会导致无聊的周期解，无法支撑复杂的信息处理。但是减小到合适的值时，将出现混沌和复杂的动力学，能遍历希尔伯特空间的所有维度。他 发现高度的自主性（独立性和动力学原理的结合）即使在一个高度开放的系统中也是可以实现的。
由上可知，Max Tegmark并未解决量子分解问题，但是这些结果可以帮助人们聚焦问题，并能强调具体的公开子问题和从观察得来的各种暗示和线索 。他还提出了一些公开的问题：
我要是说，在我们真实生活的宇宙里，时空其实是分立的而不是连续的，也许很多人会感到很惊异觉得这是一种科幻。但是一部分激进的理论物理学家的确是这么认为的，我也很认同这种观点。分立的时空格子的尺度，被称作普朗克长度和普朗克时间。首先给出它们的表达式和大小吧：
普朗克长度：
普朗克时间：
其中
首先要知道的是，目前描述我们这个宇宙的最基本最底层的理论之一是量子场论，而我们有很充分的理由相信，量子场论里存在一个物理的能量截断，即量子场论只有在能量低于这个截断能量的时候才有意义。这一段后半部分的内容直接摘抄自刘川的量子场论讲义：对于一个有相互作用的量子场论来说，由于量子涨落的“虚过程”可以在任意能动量发生，因此，如果理论不存在某种能动量截断，那么由于长是互相作用的，一个低能动量的模式就可以通过虚过程与无穷高能动量的模式发生相互作用，这就造成了场论中的“紫外发散”（即计算得到的结果是无穷大）。而如果量子场论中存在一个物理的能动量截断，它就可以保证所有的量都不发散。这个截断的具体形式其实对于远低于截断能标的物理来说并不重要，因为低能区的物理对截断的形式并不敏感。重要的是，这个截断是存在的，而且它是相互作用量子场论不可或缺的组成部分。
然后，根据不确定性关系这一量子力学的基本原理，
能动量存在着一个上截断，就意味着时空存在着一个下截断。即空间存在最小分辨率。
以上从量子场论的角度，分析了这样一个时空最小分辨率的存在性，但是并没有给出它的具体形式。其具体表达式则是由宇宙学中对量子引力极限的估计给出的。
众所周知，如果一个物体的半径相对于其质量小到了一定程度，它就会形成黑洞。形成黑洞所需要的质量和半径的关系由所谓的Schwarzschild半径给出，它是通过解Einstein方程得到的解：
另一方面，基本的量子力学知识告诉我们一个物体的de Broglie波长为：
量子引力极限的估计是这样的：当一个物体的Schwarzschild半径与de Broglie波长相当时，那么对这个物体的研究就必须知道黑洞内部要如何描述，即现有的一切物理理论都失效了，必须使用量子引力论来处理（而自洽的量子引论人类还没有建立起来）。联立Schwarzschild半径与de Broglie波长的表达式让他们相等，再加上质能关系E=mc^2和极端相对论性条件E=pc，就可以解出这个长度究竟是多大了。忽略掉并不改变数量级的常数之后，得到的结果正是：普朗克长度。普朗克时间的计算其实只要由普朗克长度除以c就可以得到。
如此一来，我们就已经清楚普朗克长度和普朗克时间的物理意义了：它确确实实是宇宙时空的最小分辨率，如果想探测比这更小的时空，你所使用的能量会如此之高以至于它自己会形成一个黑洞。
不过其实时空到底是分立的还是连续的，对人类生活一点影响都没有。普朗克长度和普朗克时间实在是太小太小，以至于夸克和电子的尺度都比它要大好几十个数量级呢。
意识是一种物质形态
今天在arXiv上读到了一篇非常有趣的论文，由MIT的物理学家Max Tegmark撰写，名为《 Consciousnessas a State of Matter》(作为物质状态的意识）。他认为，自我意识可以认为是某种物质形态，如文中的表一所示，意识必须同时包含有长期存在的状态，集成化的信息，容易写入性，以及复杂的动力学。气体，液体，固体，乃至计算机都只能满足一部分判据。
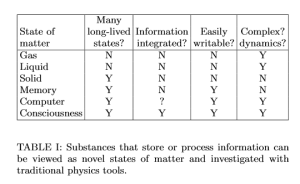为了解释意识可以被看成是物质的一种形态，他提出了六条原理，见表二
利用这些原理，他主要研究了”量子因子分解问题“，或者说作为一个有意识的的观察者，比如说我们，为什么可以感受特定的希尔伯特空间分解所对应的经典空 间，而不是傅里叶空间。或者更一般的，为什么我们把周围的世界理解为动态的层级，其中包含许多强烈集成且相对独立的物体。他认为，这个原理与所谓的从头开 始物理问题（physics-from-scratch）有关：我们如何才能从不过两个厄米矩阵中提取出三维空间和我们周围的半经典世界。能否仅从哈密顿 量H中提取出这些信息，而H完全可以仅从它的本征能谱来描述。
为了解释意识可以被看成是物质的一种形态，他提出了六条原理，见表二
接下来，Max Tegmark详细的讨论了什么叫做Integration(整体性)。在他看来，我们的世界是分层次的客体。比如说，你正在喝一杯冰水，你会感受到在玻 璃杯中有冰块。玻璃和冰块是分立的客体，因为它们都各自是一个整体且相对独立，它们内部的联系远远比与外部的联系紧密。我们可以定义物体的稳定性为集成温 度（把整体分离为部分所需的能量密度）和独立性温度（在层级内把母辈物体分离开所需的能量密度）之比。比如说，冰块的独立温度大概是3毫开，集成温度大概 是300开，稳定性是
。在下一级的结构中，氧原子和氢原子的稳定性都是10。氧原子核的稳定性是。稳定性越高，这个物体越容易被我们感知和定义。他发现，利用纠错码，经典物理允许信息基本上完全地被集成。任意一个包含至少半个比特的信息的子系统就可从剩下的比特中重建出来。存储在Hopeld neural networks (Hopeld神经网络）中的信息是天然的可纠错的。但是
个 神经元只能支持大概37个比特的集成了的信息。这就带来了一个集成化的悖论：为什么在我们意识体验所包含的信息内容似乎远大于37个比特。更糟的是，他发 现把这个结果推广到量子信息领域，反而加重了集成性悖论：量子信息系统只能支持不多于四分之一集成化的比特。实际上，对于任意大的量子系统，无论我们如何 编码，它所包含的可集成的信息都不会超过四分之一个比特。这强烈的暗示我们，集成性原理至少需要一个附加的原理作为补充。他接下来探讨了独立性原理，讨论了如何通过希尔伯特空间分解实现其对应的哈密顿量分立为互相独立的部分。他发现了量子芝诺效应悖论：如果我们把宇宙分为最 为相互独立的几个客体，那么所有的运动都会陷入中止。既然有意识的的观察者显然没有感受到任何的停滞，那么集成性和独立性原理必须还需要至少一个原理来作 为补充。
进一步的，他研究了动力学原理，因为有意识的系统不仅能存储信息，还要能处理它。他认为能量相干性（energy coherence）
可以作为动力学的合适度量，它与时间无关，且在某些纯态情况下约化为能量的不确定性。把动力学最大化只会导致无聊的周期解，无法支撑复杂的信息处理。但是减小到合适的值时，将出现混沌和复杂的动力学，能遍历希尔伯特空间的所有维度。他 发现高度的自主性（独立性和动力学原理的结合）即使在一个高度开放的系统中也是可以实现的。由上可知，Max Tegmark并未解决量子分解问题，但是这些结果可以帮助人们聚焦问题，并能强调具体的公开子问题和从观察得来的各种暗示和线索 。他还提出了一些公开的问题：
- 因子分解和鸡与蛋的问题：量子态和分解哪个先哪个后？
- 因子分解和集成化悖论
- 因子分解和时间的浮现
No comments:
Post a Comment