Thursday, February 12, 2015

stoke curl 單連通 區域D指的是由積分路經C所圍成的區域。 反之若 curlF=0，且區域D為單連通，則該積分值和路徑無關

https://www.ptt.cc/bbs/Physics/M.1253260265.A.193.html

http://mathinsight.org/circulation_unit_area_calculation


http://mathinsight.org/circulation_unit_area_calculation

curl F=0环路积分等于零 的結果 (無引號)：

區域D指的是由積分路經C所圍成的區域。 反之若 curlF=0，且區域D為單連通，則該積分值和路徑無關

※ 引述《ntust661 (Crm~)》之銘言： : curl(F) = 0 : 在任意一點 F 都存在 : 則可以稱F為保守場 這邊漏掉一個條件，除了在區域D中 F 可化為 gradf 外(也就是積分值和路徑無關)， F及其一階偏導數在區域D中的每個點必須為連續函數 此時才能說curlF=0。而區域D指的是由積分路經C所圍成的區域。 反之若 curlF=0，且區域D為單連通，則該積分值和路徑無關。 : 那以下這個勒?! : -y x : F = ──── i + ──── j : x^2+y^2 x^2+y^2 : Curl(F) = 0 ? : 畫出圖形他是明顯的渦漩場 : 他竟然不能表示出任意點的環流密度!? : 我想知道的是，他沒環流密度(旋度)在(0,0)以外嗎? : 他不是保守場卻有保守場的特性 : 怪... 考慮一個線積分如下 → → ∮ F ˙dr 這個積分值等於多少會和你的積分路徑C有關 c c為任意的簡單封閉曲線，可分為兩類討論: <1>積分路徑C不包含(0,0)，則此時C路徑所圍成的區域D中 F恆滿足 curlF=0 for every point in "this" domain D 以及 對此D內的每個點而言，F及其一階偏導數皆連續 的這兩個條件 故curlF=0，所以只和起始點以及終點有關 因此積一圈必 = 0 <2>若一任意的積分路徑包含(0,0)，則此時由C所形成的區域D 對 F來說顯然不是一個保守場!(因為D內並不是所有點都滿足保守場的兩個需求， 他只滿足 F=gradf，但(0,0)這點對F而言並不存在，當然就不連續) 因此積分值並不恆=0 又因為此時的積分路徑是任意的，所以就算你可以把該線積分grouping成 一個簡單的角度形式，你還是不知道答案是多少，如下 -ydx+xdy -1 y ∮ --------- = ∮ d(tan -) ，因為反三角函數是一多值函數，並不符合 c x^2+y^2 c x 微積分的要求。 但是我們可以透過取一個如下的路徑C*，使得C*所圍成的區域是一單連通區域 且藉此 「可將原題目中任意的路徑C變成一個我們想要的路徑(ex:圓)」 「且此時F在這個D*中為保守場」 有這兩個好處。 圖: http://0rz.tw/rlgsW 由圖可知 C* = C + AB + C1 + BA 且∫C* = ∫C+C1 (因為∫AB= -∫BA) 故得到 ∫C =∫C* - ∫C1 (a) 又因為剛剛所取的C*所圍成的區域是一個單連通區域，因為已知curlF=0 故對此不包含(0,0)的單連通區域而言，可以用Green's 定理，或由保守場， 皆可得 -ydx+xdy ∮ -------- = 0 (上述的好處之一) C* x^2+y^2 ｜ 故由(a)可得 ｜ ↓ -ydx+xdy -ydx+xdy ∮ -------- = 0 - ∮ -------- C x^2+y^2 C1 x^2+y^2 -1 y = ∮ d(tan -) -C1 x (-C1為逆時針) 這個時候因為路徑 -C1 已經明確了(一個圓形) 所以可以用極座標令 x=rcosθ，y=rsinθ (上述的好處之二) -1 y 且 r=(x^2+y^2)^(1/2)，θ=tan - 且 θ:0~2π，此時的θ是單值函數 x 2π 因此所求 = ∮ dθ = ∫ dθ = 2π。 -C1 0 -- 簡單來說，保守場要連同路徑下去考慮，因為所謂的保守場就是 和路徑無關，因此所選取的簡單封閉曲線在哪是很重要的。也就是 如果簡單封閉曲線 不含 (0,0)則它具有保守場的特性，積一圈會=0 如果簡單封閉曲線 含 (0,0)則它不具有保守場的特性，積一圈不一定=0 (就算C沒有通過奇異點也是一樣) 你沒有考慮曲線C在哪，才會有他一下子是保守場一下子不是保守場的感覺。 -- 圖換過了 D*所在位置如圖所示 -- ※ 發信站: 批踢踢實業坊(ptt.cc) ◆ From: 114.40.86.251 ※ 編輯: Mpegwmvavi 來自: 114.40.77.252 (09/18 22:05)
推 ntust661:懂!大推! 09/18 23:06
→ ntust661:以前都會以為有源頭的場才可能是保守場 09/18 23:07
→ ntust661:例如重力場，靜電場 09/18 23:07
→ ntust661:原來這種也會是保守場 09/18 23:08
→ ntust661:繞一圈作功等於零 09/18 23:09
→ ntust661:在世界上，擁有這種場嗎? 09/18 23:09
推 justsaygood:考物研所的工數,這題會考... 也會叫你解釋是否保守 09/19 00:21
→ kevin60405:我在書上看到說 無限長直導線產生的磁場 就是這種場 09/19 02:20
推 ntust661:所以磁場就是保守場了... 09/19 02:21
→ kevin60405:arctan是多值函數?高中學他的值域不是在1.4象線嗎? 09/19 02:23
→ kevin60405:如此限制可以使它成為"函數" 而不是一對多 09/19 02:24
→ nightkid:arctan是多值函數 是人為定義讓他單值化 09/19 20:09
→ nightkid:還有 所謂函數是指一個x對應一個y arctan是符合的 09/19 20:09
→ kevin60405:我印象中多值函數不是不屬於函數嗎?


Math Insight


Calculating the formula for circulation per unit area


Given the definition for a component of the curl in the direction of a unit vector, we can sketch a proof for the formula of the “microscopic circulation” that we identify with curl. For simplicitiy, we will focus on the z  -component of the curl, curlF⋅k  , which is defined as
curlF(a)⋅k=lim A(C)→0 1A(C) ∫ C F⋅ds,  
for a curve C  around the point a=(a,b,c)  in a plane that is parallel to the xy  -plane. In the above limit, we let C  shrink to a point so that the area A(C)  inside C  reduces to zero, as illustrated in the below applet. Since we divided by the area A(C)  , we can interpret curl as being a “circulation per unit area.”
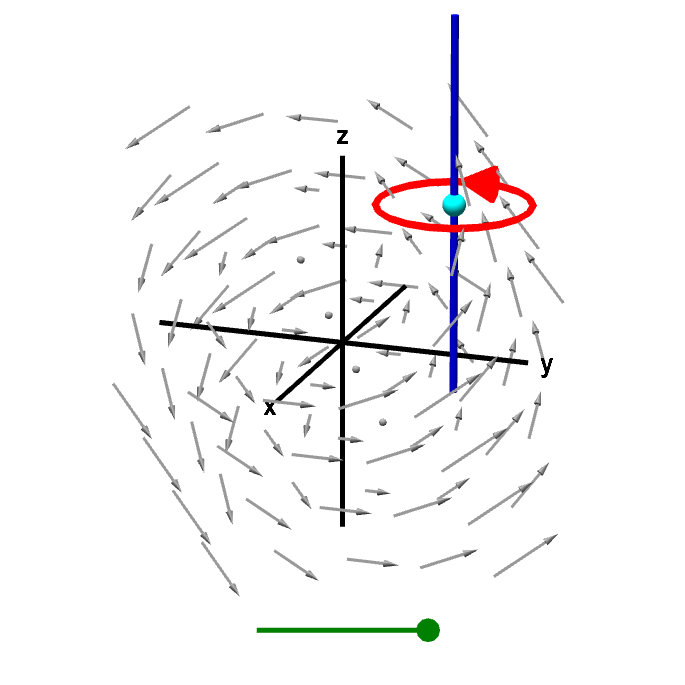Applet: A line integral gives z-component of curl
A line integral gives z-component of curl. A line integral around a curve in a plane perpendicular to the z  -axis gives circulation of the vector field corresponding to the z  -component of the curl. Dividing this line integral the the area of the region inside the curve, and letting the curve shrink to zero gives circulation per unit area. This circulation per unit area is the z  -component of the curl. You can drag the red point on the slider to shrink the curve to a point.
More information about applet.
The curve C  is contained in the plane parallel to the xy  -plane that passes through a  , i..e., the plane given by z=c  . In the integral, we can eliminate z  by replacing it with the constant value c  . Moreover, the tangent vectors along C  must be parallel to the xy  plane, which means their z  -components will be zero. Since the line integral of a vector field integrates the tangent components of the vector field, the z  -component of F  will drop out of the integral ∫ C F⋅ds  . Hence, we can, without loss of generality, replace our three-dimensional vector field F(x,y,z)  with a two-dimensional vector field F(x,y)  consisting of the first two components of the original F  evaluated at z=c  . We can then view the curve C  as lying in the xy  -plane.
Besides simplifying the notation, this change of perspective make explicit the fact that this calculation is also valid for calculating the “microscopic circulation” of two-dimensional vector fields, like we need for Green's theorem. We just need to remember that, by the right hand rule, positive values of the circulation correspond to counterclockwise rotation in the xy  -plane.
The introductory pages give some intuition why the “circulation per unit area” of the z  -component of the curl is
curlF⋅k=∂F 2 ∂x −∂F 1 ∂y .  
Here we sketch a proof why
1A(C) ∫ C F⋅ds→∂F 2 ∂x −∂F 1 ∂y   
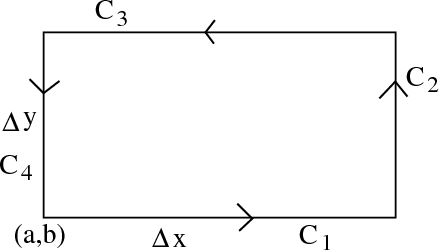
as we let C  shrink to a point. Rather than use the circular C  illustrated in the above applet, we let C  be a rectangular curve, oriented counterclockwise. For simplicity of the notation, we'll let (a,b)  be the lower-left point of C  rather than being in the middle. Let the width and height of C  be Δx  and Δy  , respectively. Label the edges of the rectangle by C 1   , C 2   , C 3   , and C 4   .
The curve used to derive a formula for the circulation per unit area
We assume the rectangle is small enough to approximate F  as constant along each edge. Along the curve C 1   , the value of y  is constantly b  , but the value of x  changes from a  to a+Δx  . We assume we can ignore that change in x  (since the rectangle is small), and simply approximate F(x,y)  as F(a,b)  all along the segment C 1   .
Along the curve C 2   , the value of x  is constantly a+Δx  , but y  changes from b  to b+Δy  . Since we assume we can ignore the change in y  , we approximate F(x,y)  as F(a+Δx,b)  all along segment C 2   .
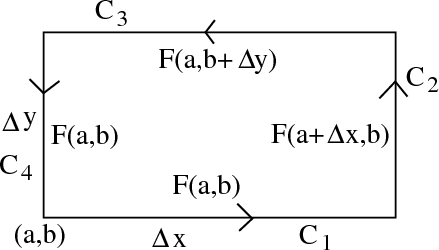
Similiarly, we approximate F(x,y)  as F(a,b+Δy)  all along segment C 3   and approximate F(x,y)  as F(a,b)  all along segment C 4   . We summarize these approximations in the following figure.
The vector field approximation used to derive a formula for the circulation per unit area
Next, to compute the integral ∫ C F⋅ds  , we remember that it is the same thing as integrating the scalar-valued function F⋅T  , where T  is the unit tangent vector along C  :
∫ C F⋅ds=∫ C F⋅Tds.  

We need to compute F⋅T  along each segment of C  . The tangent vector T  is constant along each segment, and we are approximating F  as constant along each segment, so the dot product F⋅T  will be constant along each segment of C  .
Along C 1   , the path is directed in the positive x  direction, so the unit tangent vector is T=(1,0)  . The dot product F⋅T  is simply the first component of F(a,b)  :
F⋅T=F 1 (a,b).  

Along C 2   , the path is directed in the positive y  direction, so T=(0,1)  , and F⋅T  is simply the second component of F(a+Δx,b)  :
F⋅T=F 2 (a+Δx,b).  

Along C 3   , the path is directed in the negative x  direction, so the unit tangent vector is T=(−1,0)  . The dot product F⋅T  is minus the first component of F(a,b+Δy)  :
F⋅T=−F 1 (a,b+Δy).  

Along C 4   , the path is directed in the negative y  direction, so T=(0,−1)  , and F⋅T  is minus the second component of F(a,b)  :
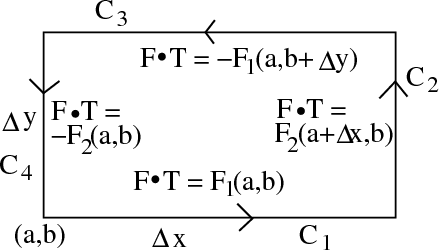
F⋅T=−F 2 (a,b).  

We summarize these findings in the following figure.
The vector field tangents used to derive a formula for the circulation per unit area
The integrals are now easy to compute. Along C 1   , F⋅T  is constant, so the integral is simply its value F 1 (a,b)  times the length of the segment Δx  :
∫ C 1  F⋅ds=∫ C 1  F⋅Tds=∫ C 1  F 1 (a,b)ds=F 1 (a,b)Δx.  
Along C 2   , the integral is F 2 (a+Δx,b)  times its length Δy  :
∫ C 2  F⋅ds=F 2 (a+Δx,b)Δy.  
Similarly,
∫ C 3  F⋅ds=−F 1 (a,b+Δy)Δx,  
and
∫ C 4  F⋅ds=−F 2 (a,b)Δy.  

The integral around all of C  is just the sum along the four segments
∫ C F⋅ds =∫ C 1  F⋅ds+∫ C 2  F⋅ds+∫ C 3  F⋅ds+∫ C 4  F⋅ds=F 1 (a,b)Δx+F 2 (a+Δx,b)Δy−F 1 (a,b+Δy)Δx−F 2 (a,b)Δy.  

The circulation per unit area is the integral divided by the area of the rectangle, which is ΔxΔy 
∫ C F⋅dsΔxΔy =F 2 (a+Δx,b)Δy−F 2 (a,b)Δy−(F 1 (a,b+Δy)Δx−F 1 (a,b)Δx)ΔxΔy .  

Half of the numerator is multiplied by Δy  and half is multiplied byΔx  . If we separate these into two fractions, we can cancel the Δy  in the first fraction with the Δy  in the demoninator
F 2 (a+Δx,b)Δy−F 2 (a,b)ΔyΔxΔy =F 2 (a+Δx,b)−F 2 (a,b)Δx .  

In the second fraction, we can cancel the Δx  ,
F 1 (a,b+Δy)Δx−F 1 (a,b)ΔxΔxΔy =F 1 (a,b+Δy)−F 1 (a,b)Δy .  
Putting these back together, we have
∫ C F⋅dsΔxΔy =F 2 (a+Δx,b)−F 2 (a,b)Δx −F 1 (a,b+Δy)−F 1 (a,b)Δy .  

Now, we let the curve C  shrink down to a point. This means that Δx→0  and Δy→0  . In this limit, the two fractions become something familar: partial derivatives of F  .
lim Δx,Δy→0 ∫ C F⋅dsΔxΔy  =lim Δx→0 F 2 (a+Δx,b)−F 2 (a,b)Δx −lim Δy→0 F 1 (a,b+Δy)−F 1 (a,b)Δy =∂F 2 ∂x (a,b)−∂F 1 ∂y (a,b).  

Therefore, the circulation per unit area around the point (x,y)=(a,b)  is
∂F 2 ∂x (a,b)−∂F 1 ∂y (a,b).  
This is the expression for the scalar curl that we use for the “microscopic circulation” in Green's theorem. If we rewrite this in terms of the original three-dimensional vector field F(x,y,z)  at the point (x,y,z)=(a,b,c)  , we obtain the expression for the z  -component of the curl
curlF(a,b,c)⋅k=∂F 2 ∂x (a,b,c)−∂F 1 ∂y (a,b,c)  
as promised.

Thread navigation

Math 2374
Multivariable calculus

Notation systems


More information on notation systems

Similar pages



See also


Lighten up



Posted by at

No comments:

Post a Comment

Subscribe to: Post Comments (Atom)