无法将幅度和相位统一表述 2) 做Cos或者Sin的运算会非常繁杂.
sun_ic的个人空间http://home.eeworld.com.cn/?355576 [收藏] [复制] [分享] [RSS]
日志
电路设计漫谈之66: 负频率是怎么来的?
||
做信号处理或者频谱分析时, 总是遇到负频率的概念. 当年学这个理论, 在Fourier变换时作为一个函数的偶对称自然引入了, 虽然觉得奇怪但也没人追究, 记住那些方程变换等还来不及呢, 管它负频率什么意义了. 若干年之后用这一工具来解决一个 实际问题时, 不免对这个负频率的来历想追究一下. 它的物理意义是什么,为什么要引入这个概念.
本人翻阅了Morris Kline 的古今数学思想,还有一日本教育基金用漫画形式写的Who Is Fourier, 以及感觉最有帮助的Richard Lyons的understanding Digital Signal Processing. 终于对这个负频率的来历有了一个较为清晰的轮廓.原来在诸多专业和业余数学家们, 尤其欧拉没进来搅和之前, 一个通常的实际信号是可以没有负频率的,如下图1所示. 一个实信号只用一个实频域的频点表示即可 (当然还得另外表示相位,这也是后来引入复频域的好处). 即使用Fourier变换, 也可以把一个实信号表示成只具有实数的Sine/Cos级数或者积分变换. 这样一切频谱分量都是正的, 即级数n或积分区间取正.

上边的表述是显而易见的, 但有两个不方便的地方 1) 无法将幅度和相位统一表述 2) 做Cos或者Sin的运算会非常繁杂.
伟大的欧拉建立起了复指数与Sin,Cos的对因关系 exp (jwt)= coswt + jsin(wt). 高斯和之前的一些业余数学物理学 家对复数理论 也有很大贡献. 复数的引入使得相位和幅度被统一到一个表达上,并且数学运算也方便多了. 但代价是得引入负频率这个怪异的 东西.
图2是一个复指数信号的时域与复频域的表示方法.一个复平面上随时间旋转的点就是一个周期复指数信号的轨迹. 引入j 代表”垂直”分量 (最好别叫它虚数,而是称为一个旋转算子), 一个巧妙的解释就是当一个数乘以j后, 就代表其向量在复平面逆时 针旋转90度. 同理乘以-j就是顺时针旋转90度 (-j=j*j*j, 相当于逆时针旋转三次). 1是实轴上一个数,乘以j旋转90度就变到j轴成为1j, 再乘以j再旋转90度就变成 -1. 所以在实轴上的sin(wt)乘以j后就变到j轴了. 这个解释是18世纪一个瑞士自学成才的记录员Argand 提出的.
复信号在时域中表示: 水平轴是一个cos分量, 垂直轴是个sin分量. 在复频域中表示, 逆时针旋转的是一个正频率分量. 顺时针旋转的是一个负频率分量. 这是负频率的根本来源.

周期复数信号也可以找到实际信号的对应. 比如经常举的一个示波器的例子. 信号通道(水平轴)接Cos信号. 触发通道 (垂直轴 ) 接一个同相sin信号,也就是构造出图2的各个分量,那么在屏幕上显示的就是逆时针旋转的一个点.
用复平面来表示一个实数信号, 通过欧拉公式变换一下是可能的, 参见图3所示. 但这样一来一个简单的cos 就要表示成两个复指 数的信号了, 一个是复时域逆时针旋转的具有正频率, 一个是复时域顺时针旋转的具有负频率. 从图2也很容易看出, 这两个复信 号在 j 轴的分量方向相反, 相加后抵消, 只剩下实轴的cos分量.
图3的左图是cos信号在复频域上的表示. 对于sin信号在复频域的表示要稍微做点变换,也就是j算子的旋转功能: 负频率分量乘以j逆时针旋转一次. 正频率分量乘以-j: 先逆时针旋转90度,再逆时针旋转90+90度 (-1 = j * j). 或者视为 –j = j* j*j, 逆时针旋转三个90度. 所以负频率的表示,完全是由于引入了复数的原因. 有道是: 菩提本无树, 明镜亦非台J.
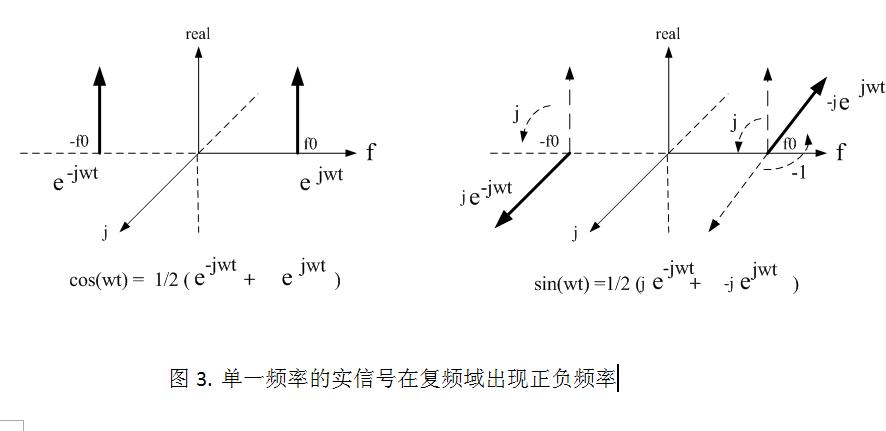
单一频率的时域信号比如cos和sin在复频域表现为正负对称的两个复数频率. 单一频率的复信号在复频域是单一频率,但在时域需要两个正交分量表示.
一般教科书论述负频率引入是在做积分变换时, 利用函数的对称性, 把(0, +无限) 对exp(-jwt)运算, 改为 (-无限, 0) 对exp(jwt) 的运算 , 然后就出来负频率了. 窃以为这很不负责然. 欧拉和之前Argand引入的旋转算法, 也就是richard在其书中所描述的负频率使用的方法, 是具有物理意义的理想表述.
本人认为频谱的实际物理意义, 应该是被分析信号与每个可能频率的相关程度的衡量 . Fourier变换可以认为是信号对每个周期波形求其全时域的相关性. 如果是一个1KHz的余弦实信号, 它跟以1KHz震荡的cos(2*pi*1000*t)信号相关度为1(不考虑相位的话), 跟其它频率的相关度是0,所以这个信号的频谱就是1KHz. 一个复杂的信号,跟每个频点的cos信号都有一点相关, 所以频谱就是一个频域0到无限的连续曲线. 记得光波导理论,用来分析光”波形”的变换是空间变换, 就是把光波形相关到每个空间基本单元,然后研究其”空间谱”的分布. 所有的这种变换,都是为了变换到一个域, 其运算比时域更简单,也更容易衡量其特性.
为什么任何信号都能表示为Sin和Cos函数的组合呢? 当然电信号的表述来自于电磁波的Maxwell方程. 其解就是波动的. 但如果YY一下, 感觉量子力学的波动性才是根源. 任何物理存在都是薛定谔方程的解. 所以电信号本质是是波动的组合,应该能表示成若干基本波动的组合.
顺带转述一下, 古今数学思想中介绍Fourier积分起源于寻求偏微分方程的封闭解. Klein说Fourier积分的发明权现在无法定论. 因为Fourier(傅立叶), Cauchy(柯西), Poisson(泊松) 三人都向巴黎科学院宣读了之后才发表的论文, 这里都涉及了Fourier积分, 而每个人都听过别人的论文. 但最早Laplace所做的奠基性工作则无异议.
No comments:
Post a Comment