《硅火燎原》-28-AB效应和贝里几何相
|||
28. AB效应和贝里几何相
1982年,美国华盛顿大学物理学家索利斯(D.J.Thouless)等人,为了直接表征量子化霍尔电导的填充因子n,引入了一个称为TKNN的拓扑数,并由此而对电子波函数的拓扑性质进行分类【1】。这是第一次将数学上的拓扑概念应用于与‘相’有关的凝聚态理论中。
拓扑概念如何与量子态关联起来了呢?这还得从近几年物理中的一个新进展,称之为‘贝里相位’的概念说起。贝里相位又与AB效应密切相关。
所以,有必要首先简略介绍下什么是AB效应。
量子力学中有一个著名的杨氏双缝电子干涉实验【2】。在杨氏双缝实验中,电子通过两条狭缝后,在荧光屏上出现干涉条纹,从而证实了电子的波动性。如今我们不详谈这个实验本身,而是将它借来解释AB效应。
如图28.1a所示,电子波同时穿过两个狭缝后,从A点发出的子波和从B点发出的子波,假设它们到达屏幕上的C点时互相干涉而加强,便会在C点形成一个亮点。整个波的总效应则是在屏幕上出现明暗相间的条纹。然后,我们设想,如果将实验稍微改变一下,成为如图b所示:在两个狭缝间靠近狭缝处,插入一个非常细无限长的通电螺线管。这时候,实验结果会发生变化吗?
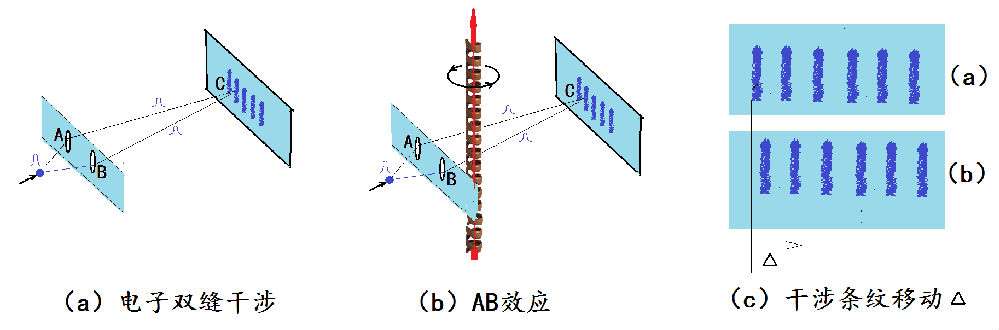
图28.1:磁AB效应
首先我们从经典电磁场理论的观点来分析这个问题。在理想情况下,因为通电螺线管是无限长的,图中所示方向的电流将会在线圈之内产生一个从下往上的磁场。但是,紧密缠绕的螺线管将磁场完全包在了它的内部,线圈之外的磁场将处处为0。电子不会进到线圈以内,所以,经典理论认为,电子应该感知不到磁场的存在。当然,实际上,如果将电子看作是不具有波动性的经典粒子的话,屏幕上不会出现明暗相间的干涉条纹,而是按照经典几率的分布图像而已【2】。总而言之,根据经典电磁理论,放(或不放)这个通电螺线管,对电子的实验结果不会产生任何影响。
不过,如果用量子理论来计算,却会预期一个不同的结果,这便是1959年英国两位理论物理学家阿哈罗诺夫(Aharonov)和波姆(Bohm)所作的工作【3】。他们认为,通电螺线管的存在会使原来的干涉条纹产生移动,像图28.1c所显示的那样。如果通过螺线管的电流反向,干涉图像移动的方向也会反向。
在阿哈罗诺夫和波姆的文章中,他们不仅进行了理论计算,还详细设计了验证的实验。之后的近30年内,有许多人进行了与此相关的实验,得到A和B预期的结果。但是,物理学家们却总是对此理论及实验结果争论不休,一直到了1986年,日立公司的科学家Tonomura等人的实验【4】,才终于得到了学术界的最后认可。至今,又过去了二十多年,AB效应已被物理学界完全肯定,并写入了教科书, 成为量子力学教材中不可缺少的基本概念。
阿哈罗诺夫-波姆效应之所以引起重视,是因为它证明了在量子理论中电磁势(包括矢量A及标量势r)的重要性,以及与其相关的电子波函数的相位的重要性。
经典的麦克斯韦方程是定域性质的微分方程。这种定域的描述方式是很容易得到公认的,如此描述的物质间的相互作用是由场传递的接触作用。它克服了‘超距作用’的困难,将带电粒子运动状况的变化归结为每一点的场对它逐点作用的结果。麦克斯韦方程表示电磁场有两种形式:可以用场强(电场E、磁场B)来描述,也可以用电磁势(三维矢量A、标量势r)来表示。但是,经典电磁理论认为,只有第一种方式使用的,空间中每一点的电磁场的强度,以及它使得运动电子经过该点时所受到的电磁力,才是基本的,才具有可观察的物理意义。而第二种方法中的电磁势(A、r),不过是为了计算方便而引入的数学概念,并不代表物理实质。以规范变换为例便能说明这一点:电场和磁场是规范不变的,而电磁势在不同的规范下则取不同的值,这是经典理论认为电磁势不是物理可观察量的理由。
什么样的量在物理学中是基本的,代表物理实质呢?举个简单例子让你更深入理解这点。
几万伏特的高压电线是很可怕的,但是,停在上面的鸟儿却仍然活蹦乱跳,丝毫感受不到危险,大家都知道这是为什么。那是因为我们是站在地面上,高压线的电压相对于地面的数值很高。尽管如此,但在鸟儿能接触到的局部小空间范围内,这个值却没有什么物理意义。鸟儿能感受到的、对它能表现物理效应的,是它两只脚两点间的电压差,而不是某点电压对地的绝对数值。
因此,对鸟儿来说,完全可以作一个电压的平移变换(V->V’),将电线上某点的电压值设为0。这样来研究问题,计算要简单些。因为有物理意义的电压差(V1-V2)是在平移变换中保持不变的,所以鸟儿感受到的物理效应在变换下将没有任何区别。电磁理论中的规范变换呢,与此有点类似,只不过那时需要将电场磁场统一考虑。换言之,需要将矢量势和标量势一块儿变换。也就是说,用(A、r),或者用另一组规范变换后的(A’、r’),都表示同样的电磁场(B、E)。规范变换当然比鸟儿问题要复杂许多,但却同样也能起到简化计算,保持物理基本量不变的效果。
再回到实验中电子运动的问题。从经典电磁理论看,既然只有场强E和B才有物理效应,而在电子运动的路径上,线圈外所有点的电磁场场强(E和B)都为0,线圈对电子的运动当然不会有影响。
那么,AB效应又该如何解释呢?
从量子力学的观点看,电子具有波粒二象性,它的运动用波函数来描述,这是量子理论与经典理论的根本区别。任何波动,除了振幅之外,还有相位。图28.1a中屏幕上的干涉条纹,也就是从A和B经过两条路径的电子波之间的相位差而产生出来的。
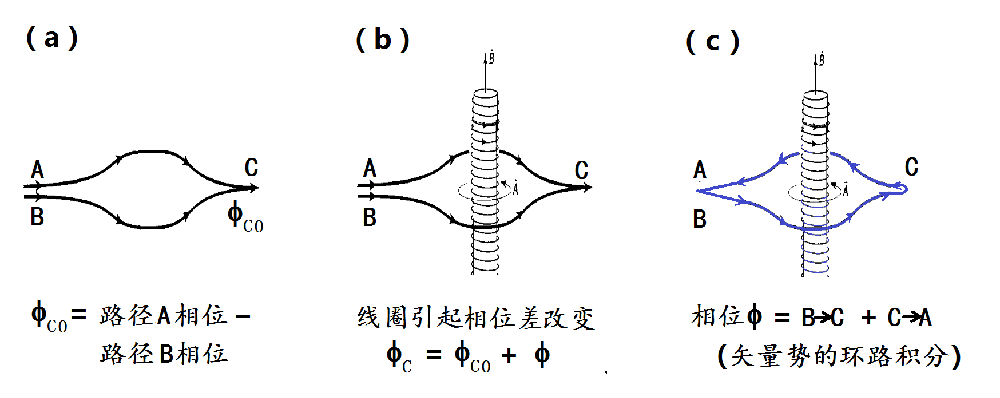
图28.2:磁AB效应中通电线圈引起的相位因子f
现在,放了通电线圈之后,实验中观察到干涉图像产生了移动。那说明A路径和B路径之间的相位差发生了变化。没错,如果我们用量子力学的理论,分别在没线圈和有线圈的时候进行计算,的确发现通电线圈的存在,在两条路径中引入了一个额外的相位因子。就像图28.2中图a和图b的情况,相差了一个相位因子f。
你可能会说:“这不就解释了AB效应吗?条纹移动是由f产生的!”而正是这个f困惑着物理学家们,并为此争论许多年。为什么呢?因为算出来的这个相位因子,与电子经过路径上的电磁场强度无关,而是与他们原来认为不是物理实在的电磁势(A、r)有关的。实际上,它就等于矢量势A,沿着路径B到C,然后再从C返回B,绕线圈转一圈的环路积分。(在这儿,我们将靠得很近的A和B算作了同一个点B。)
那么,如果认可AB效应的实验结果,原来对电磁势的看法就要重新考虑。电磁势可能在某种意义上也代表了物理实在哦!换言之,仅仅用场强来描述电磁现象似乎还不够,得把电磁势加上去。但是,这儿又有问题了,刚才说了,电磁势不是根据规范的选取而变化的吗?选取不同的规范,可以使某些点的矢量势变成0,这样我们才能使运算简化嘛。那么,到底是该用(A、r),还是(A’、r’)呢?一个连数值都不能确定的量,又该如何谈到它的实在的物理意义呢?
想来想去、争来争去,真理总是越辩越明朗。尽管规范变换的确会使得某些点的矢量势变为0,但事实上,只要线圈中有电流,即使线圈外每点的场强都是0,却绝不可能使所有点的矢量势都变成0。此外,虽然每一点的矢量势是规范变化的,但仍然可能有一个与局部点的电场磁场无关,而只与路径上电磁势有关的某个东西是规范不变的。对啦,很可能就是那个矢量势的环路积分,也就是那个相因子f,它应该是规范不变的。
因此,AB效应又使得人们重视起相位这个东西。
接着,在1984年,物理学家们尚未完全认可AB效应之时,英国布里斯托尔大学跳出来一位叫迈克尔·贝里(SirMichael Victor Berry,1941-)的数学物理学家。贝里向物理学家们发出警告:一个量子体系随参数缓慢变化再回到原来状态时,可能会带来一个额外的相位因子。贝里认为这个相位因子不是由动力学产生的,而是由(某个)空间的几何性质而产生的,因此称之为几何相位【5】。此外,贝里证明了这个相位因子是规范不变的,因而它很有可能具有可观察的、不可忽视的物理意义。贝里认为,AB效应便能用这个几何相位因子来解释。
借用网上一个比喻,贝里的意思是说,在倒掉洗澡水的时候要小心哦,里面可能有小孩!
贝里洗澡水中有小孩吗?且听下回分解。
参考资料:
【1】Quantized Hall Conductance in aTwo-Dimensional Periodic Potential,D. J. Thouless, M.Kohmoto*, M. P. Nightingale, and M. den Nijs,Phys. Rev.Lett. 49, 405–408 (1982)。【2】作者科学网博文《走近量子纠缠》- 杨氏双缝电子干涉实验:
http://blog.sciencenet.cn/home.php?mod=space&uid=677221&do=blog&id=534092
【3】Aharonov, Y.; Bohm D. (1959)."Significance of electromagnetic potentials in quantum theory". Phys.Rev. 115: 485-491.
【4】Osakabe, N., T. Matsuda, T. Kawasaki, J.Endo, A. Tonomura, S. Yano, and H. Yamada, "Experimental confirmation ofAharonov-Bohm effect using a toroidal magnetic field confined by asuperconductor." Phys Rev A. 34(2): 815-822 (1986).
【5】M. V. Berry (1984). "Quantal PhaseFactors Accompanying Adiabatic Changes". Proc. R. Soc. Lond. A 392 (1802):45–57.
【6】石墨烯中的贝里相位:Jiamin Xue, arXiv1309.6714 (2013).
http://blog.sciencenet.cn/blog-677221-741018.html
上一篇:《硅火燎原》-27-解读量子霍尔效应
下一篇:《硅火燎原》-29-洗澡水中的小孩
13 李伟钢 杜敏彪 应行仁 郭向云 田云川 文克玲 罗会仟 石磊 薛加民 杜增义 aq22 vivikzw Allanmu
该博文允许注册用户评论 请点击登录 评论 (7 个评论)
- [7]Allanmu
- 这样的好文,决定推荐给孩子看看. 看不懂也不觉得枯燥

- [6]田云川
- 好文!
标量势和我讲的T物质的密度分布可能是相似的:http://bbs.sciencenet.cn/home.php?mod=space&uid=531273&do=blog&id=715005 - 博主回复(2013-11-13 20:40):有意思
- [5]李铭
- 建议补充杨振宁和 TT WU在1975年提出的电磁场的不可积相因子的理论。这个理论对电磁势有更准确的表述。
- 博主回复(2013-11-12 23:06):谢谢建议
- [4]yao101yao
- 看不懂
- 博主回复(2013-11-12 23:05):

- [3]郭威
- Berry Phase 没拿诺奖真是可惜 。。。
- 博主回复(2013-11-12 23:05):还有机会
- [2]杜增义
- NC问题:贝利相有怎样的拓扑性质?!
- 博主回复(2013-11-12 23:04):下次会讲。
- [1]mirrorliwei
- 也许直接介绍Tonomura等人的实验比抽象的表述更为精彩。
- 博主回复(2013-11-12 23:03):

《硅火燎原》-29-洗澡水中的小孩
|||
29.洗澡水中的小孩
贝里是在研究量子混沌的时候发现贝里相位的。有人说,贝里并不是发现几何相位的第一人,但无论如何,贝里让人们重新认识到几何相位的重要性,比如,是在贝里文章的启发下,才发现了经典力学中的对应物:Hannay角【1】。了解和解释几个经典的例子可以使我们更容易理解量子力学中的几何相位。
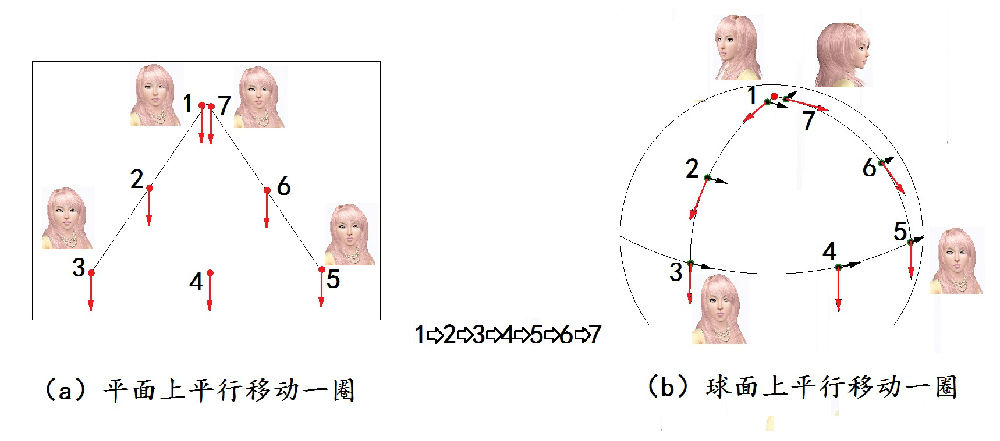
图29.1:矢量平行移动一周后的变化(a)平面(b)球面
图29.1是在平面和球面上分别作平行移动的例子:女孩从点1到点2再到点3,一直到点7,作平行移动一圈后回到点1(1和7是同一点)。所谓‘平行移动’的意思是说,她在移动的时候,尽可能保持身体(或是她的脸)相对于身体的中心线没有旋转。这样,当她经过1、2、3……回到1的时候,她认为她应该和原来出发时面对着同样的方向。她的想法是正确的,如果她是在平面上移动的话(图a)。但是,假如她是在球面上移动的话,她将发现她面朝的方向可能不一样了!图b中红色箭头所指示的便是她在球面上每个位置时面对的方向。从图中可见,出发时她的脸朝左,回来时却是脸朝右。这是怎么回事呢?关键是球面与平面不同的几何性质起了决定性的作用【1】。
所以,从上面的例子得出一个结论:贝尔所说的“洗澡水”中有时有小孩,有时没小孩。在上述的例子中,如果在平面上“洗”(平行移动),洗澡水中没小孩。但如果是球面上洗,那就要小心了,不要糊里糊涂地把水给倒了,可能有个小孩在水里!
这个例子中,我们说,矢量方向改变的效应是几何的,不是动力的。怎么样改变就算是动力的呢?比如说,女孩自己将身体旋转,扭来扭去,或者是在移动的过程中,被别的人或物体碰撞而产生了方向变化,或者说,女孩是在风中移动,状态随时间而改变积累起来的方向变化等等,都应算是动力性质的。除去这些因素,只是因为经过路径所在的空间的几何性质,如前所说的平面或球面而造成的方向改变,就是几何的了。
像平面这种几何曲面,还包括可以展开成平面的柱面和锥面等,在经典力学的意义上,被称之为“平庸”的。反之,如像球面或马鞍面之类,不弄破就不可能铺开成平面的那种曲面,则是不平庸的。
刚才是经典比喻,在量子世界中的贝里相位也是这样,有时是0,可以忽视;有时则不能忽视,比如上一节中介绍的AB效应,实际上就是一个不可忽略的贝里相位。
什么时候可以忽略,什么时候不能忽略,则取决于路径通过的空间的几何性质。

图29.2:迈克尔·贝里和他研究的“磁悬浮青蛙”
迈克尔·贝里除了因提出几何相而出名之外,还因为与安德烈·海姆研究“磁悬浮青蛙”,而获得2000年的搞笑诺贝尔物理奖(Ig Nobel Prize for Physics)【2】。安德烈·海姆后来因为对石墨烯的开创性实验研究而获得2010年诺贝尔物理奖,贝里也曾得到过沃尔夫物理奖等多种奖项。由此可见,搞笑诺贝尔奖也不仅仅是一种戏谑调侃,可能更多的是体现了一种幽默,得奖者中也不乏创意之人,比如贝里就应该可以算作一个。
回到上节中介绍的AB效应。AB效应中得到的不可积相位因子,根源是来自于那个细长的螺线线圈。线圈中的磁通量改变了空间的拓扑性质。没有磁场时,空间是平庸的、单连通的普通三维空间。首先简单地解释一下什么是“单连通”:如果一个区域中的任何一条闭曲线,都能连续地收缩到区域中任何一点,此区域便被称为单连通的。以图29.3的二维图形为例,图a淡蓝色图形中的任何曲线,例如与图中那条从B出发、到C、再回到B的类似曲线,都可以连续地变小而收缩到任何点。这说明那块淡蓝色图形是“单连通”的。但是,如果在这个区域中挖一个或几个洞,成为像图b所示的淡蓝色区域,情况便会有所不同。如果区域中的某条闭合曲线,有“洞”被包围其中的话,就不可能连续收缩到一个点了。这种图形空间便成为“多连通”的,也就是拓扑非平庸的了。
在AB效应中,通电螺线管的存在相当于在电子运动的三维空间中挖了一个洞,使空间变成了非平庸的,也使得电磁矢量势绕着螺线管积分一圈后,出现了一个不可积的相位因子。也就是贝里所说的不可与洗澡水一起倒掉的“小孩”。
再深究下去,物理学家们更感到眼前豁然一亮:那个相位因子f,并不是与每一点的局域电磁场(或电磁势)有关,而是与电磁势绕环路一圈的积分有关,这说明了什么呢?比较微分而言,积分体现的是一种整体性质。那么,这就说明AB效应不是一个局部效应,而是电磁势产生的一个整体效应【3】。

图29.3:单连通和多连通
因此,Berry几何相因子的研究使人们认识到量子系统(乃至经典系统)的整体性质的重要性,这也就是如今它成为了量子理论中一个普遍存在的重要概念的原因。在数学上能描述空间整体性质的理论就是拓扑学。如刚才所述,利用电磁场空间的连通性质便能解释经典理论难以解释的AB效应,那么,也许还有许多奇妙的量子现象,可能都和空间的拓扑性质有关系,或许能用整体拓扑的概念来解释它们。
事实上的确是这样。不过,刚才我们经常说到的“空间”,则远远不是仅限于我们生活于其中的三维空间了。量子理论中“空间”的概念是多样化的,可以是真实的4维时空,也可以是相空间、晶体的倒格子空间、布里渊区,以及所谓系统的内禀空间,包括自旋空间、描述系统哈密顿量的参数空间、波函数的希尔伯特空间等等。到底需要考虑哪个空间的几何拓扑性质,必须根据具体问题而具体分析。
比如说,在量子理论中,一般用希尔伯特空间来描述量子态。如果考虑一个在真实的三维空间中运动的电子,对应于电子轨迹的每个点,都存在一个与波函数相应的无穷维的希尔伯特空间。由此我们可以建立一个数学模型,将电子真实运动的空间作为基空间,希尔伯特空间作为切空间,如此就构成了一个数学家称之为“纤维丛”的东西。上世纪70年代,理论物理学家将纤维丛与规范场论对应起来【4】。如果来个通俗比喻的话,纤维丛可以直观地理解为如图29.4左图所示的图像:一根作为基底的铁丝上缠绕着许多根纤维(毛线),或者是想象成凸凹不平的泥土地上长满了长长短短的杂草。这样一来,在纤维丛所描述的量子理论中谈到空间是否“平庸”的问题时,就需要考虑这个复杂的“纤维丛”空间是否平庸的问题了。这儿包含了基空间、纤维空间、还有纤维丛空间三者的几何性质:铁丝弯曲成了什么形状?泥土地是平面还是球面?毛线或杂草(对应着希尔伯特空间),是简单而平庸的形态,还是某种卷曲、打结等古怪的样子?还有纤维丛本身,也可能是整体非平庸的,像29.4右图所示的莫比乌斯带那种。有关纤维丛的更深入介绍,可见参考文献【5】。
总之,贝里相位的发现使物理学家们从拓扑的、整体的观点来研究物质的不同形态。这对凝聚态物理中近年来发现的各种量子相变现象的研究特别有用。因为原来研究相变时所使用的朗道自发对称破缺理论不适用了。如前面讨论过的量子霍尔效应,不同的整数(或分数)霍尔量子态,具有完全相同的对称性,即不能用对称破缺来解释这些态之间的互相转变。实际上,不同的霍尔量子态对应的是不同的拓扑不变量。如整数量子霍尔效应中的整数n,便是与二维电子气系统的哈密顿量所依赖的二维参数空间的拓扑性质有关,这个拓扑性质可以用一个非0的、以数学家陈省身命名的不变量—“第一陈数”来表征。
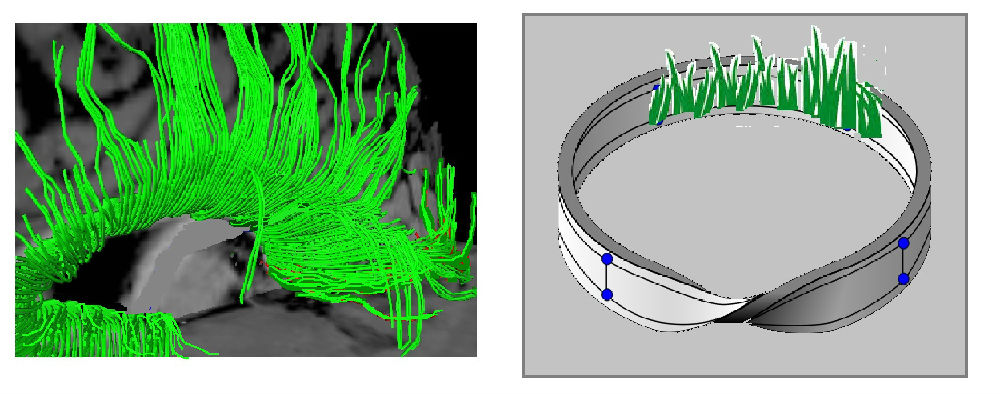
图29.4:纤维丛的直观图像
量子理论中还有一个有趣的问题,那是有关复数的用途。杨振宁在一次演讲中谈到关于从-1开方而得到的虚数i,他说:“虚数i以前在物理中也出现过,可是不是基本的,只是一个工具。到了量子力学发展以后,它就不只是个工具,而是一个基本观念了。为什么基础物理学必须用这个抽象的数学观念:数i,现在没有人能解释。”
虚数i的使用应该是和相位的概念密切相关的。虚数i的重要性说明电子的波函数不仅仅包含了电子在空间出现的概率的信息,更为重要的是包含了不可忽略的相位的信息。相位是量子理论的真正本质所在。
文小刚继提出拓扑序(Topological Order)之后,又将其扩展到更一般的“量子序”的概念,再次强调相位对区分量子序和经典序的重要性【6】。
100多年前,发现未知的新元素是科学的热点。建立了基本粒子物理学之后,预言和发现新的基本粒子,成为物理学的热点。2013年的诺贝尔物理奖授予了预言希格斯粒子的几个物理学家,就是基于2012年CERN科学家们的实验,它发现并证实了标准模型中最后一个基本粒子--“上帝粒子” 的存在。当前,凝聚态物理之所以成为物理学之热点,则与近年来不断预言和实验证实的新的量子物态密切相关。因为新物态的浮现既有理论意义,还可能在自旋电子和量子计算等领域具有实用价值,有时还能导致意想不到的思想上的突破甚至物理及数学理论上的革命。对此,我们将拭目以待。
参考资料:
【1】Hannay J H 1985 Angle variable holonomy inadiabatic excursion of an integrable Hamiltonian J. Phys. A: Math. Gen.18 221–30.【2】http://en.wikipedia.org/wiki/Ig_Nobel_Prize
【3】《简单物理系统的整体性:贝里相位及其他》,李华钟著,上海科学技术出版社,1998。
【4】杨振宁:20世纪数学与物理的分与合
【5】Yvonne C.B.,Cecile D.M.,Margaret D.B.,1977,”Analysis, Manifolds, and Physics”,North Holland Publishing Company, Amsterdam.
【6】Xiao-Gang Wen, Quantum Field Theory of ManyBody Systems - From the Origin of Sound to an Origin of Light and Electrons,Oxford Univ. Press, Oxford, 2004.
上一篇:AB效应,几何相
http://blog.sciencenet.cn/blog-677221-742938.html
上一篇:《硅火燎原》-28-AB效应和贝里几何相
下一篇:《硅火燎原》-30-拓扑绝缘体简介
28 王涛 许培扬 罗会仟 杜敏彪 王伟 应行仁 王国强 田云川 鲍海飞 徐晓 戴明哲 刘全慧 罗德海 李志军 孟利军 徐耀 林涛 李伟钢 石磊 徐洪亚 薛加民 lengyonggang EroControl biofans Allanmu goett wangqinling vivikzw
该博文允许注册用户评论 请点击登录 评论 (14 个评论)
- [14]shenlituo
- 不过还是要立顶张老师渊博的知识,上知高深物理,下知高深数学。。要是能和张老师合作算模型 我觉得我的PRL估计现在可以厚厚一叠了。。
- 博主回复(2013-12-5 00:00):过奖了,谢谢。
- [13]shenlituo
- 所说的这几个例子是AA相,当然我想所有的量子几何相位也好,AA相位也好,只要存在对应的数学理论,应该都能很好的解释。难点在于具体物理系统的量子态有时太复杂,无法求得解析解。。。
- [12]宁进良
- 哇塞 原来trivial 和nontrivial是这个意思啊 十分感谢张老师
- 博主回复(2013-11-24 06:18):实际上,trivial 和nontrivial的定义不是所有场合都一致的。比如球面,在文章所举的经典例子中,是nontrivial的,但是如果从“连通”性质看,它是单连通,不是多连通的。因此,trivial 和nontrivial只是相对而言。
- [11]goett
- 无论是量子还是拓扑,洋人在知道其根本的模型的基础上进行着研究,我们的人是以洋人的研究者为模型来研究与学习。 您何时能将这个标准的模型给大家先拿出来?,而后再解释每个部分......。
- [10]Allanmu
- 给张老师鼓个掌, 感谢您的一路牵引.

- [9]mycheng
- 很喜欢您的博客!特来拜访!
刚看到一个帖子,EI检索免费查询:http://www.sjz5.com/read/6626 推荐给您!祝好!
- [8]田云川
- 好文!
- [7]hillyuan
- 关于平行的定义有点暧昧
=>尽可能保持身体(或是她的脸)相对于身体的中心线没有旋转
这个如何?
http://hillyuan.blogspot.com/2013/08/blog-post.html
- [6]郭威
- Berry phase 在极化的近代理论中有很重要的应用,石墨烯拿奖实在太神速了。。。
- [5]谢立
- 自己懂,是大牛 ;自己懂了,还能让别人懂,是大牛+大师。前者是一种自我的成就,而后者更是一种社会价值的实现。所以,本文作者这一系列科普文章的创作,比之于在杂志上发两篇paper更有意义。在感谢作者的同时,希望作者能将这种惠及众人的做法继续下去,相信,像我这种从这一系列文章中获取了营养的读者们是不会忘了您的。
- 博主回复(2013-11-24 06:10):谢谢捧场。
- [4]杨波
- 太猛了,通过科普打通前沿

- [3]EroControl
- 概率,相位,时空函数只能这样的途径来描述么? 缺了点什么的感觉。
惯例啰嗦:好文章,谢分享,太深奥,收藏看,帮顶。 - 博主回复(2013-11-24 06:09):>>缺了点什么的感觉。
作为科普,难以面面俱到。
- [2]符建
- 写得漂亮
- [1]罗会仟
- 老杨现在还搞不搞纤维丛? 记得当年大学时候硬是没学懂。
No comments:
Post a Comment