惯性是头倔驴
||
物体具有保持自己运动状态不变的性质,我们把这一性质叫做惯性。惯性的大小只跟物体的质量有关系,是物体的固有属性。
为了说明固有属性是个啥玩意儿,我们讲一个月亮驴子的故事吧。月亮在绕着地球转动,像一头驴子在绕着磨盘转动,所以我们叫他月亮驴子。显然,做圆周运动的月亮驴子,其运动方向在不断的变化,也就是说其运动状态在不断的变化。能改变物体运动状态的一定是力。地球对月亮驴子的引力像牵着驴子的缰绳一样改变着月亮驴子的运动状态。
虽然月亮驴子不得不服从于缰绳的意志,但是这不是月亮驴子的本性。即使是这个时候,月亮驴子的本性也是不变的,他有做匀速直线运动的欲望。可见,惯性就是倔驴的“倔脾气”,跟外力没有关系。一旦缰绳没有了,所有的力都撤销,或者抵消,月亮驴子必将显露出其本身固有的属性,做匀速直线运动或者静止,这就是牛顿第一定律。
根据等效原理,如果我们定义“自由落体惯性系”,那么我们就可以不把引力看成是力,而是几何。也就是说,所有关于引力的信息都可以用时空的弯曲来描述。时空可以对应在一张全息屏上,这大概就是全息原理吧
熵力,逗你玩
为了说明固有属性是个啥玩意儿,我们讲一个月亮驴子的故事吧。月亮在绕着地球转动,像一头驴子在绕着磨盘转动,所以我们叫他月亮驴子。显然,做圆周运动的月亮驴子,其运动方向在不断的变化,也就是说其运动状态在不断的变化。能改变物体运动状态的一定是力。地球对月亮驴子的引力像牵着驴子的缰绳一样改变着月亮驴子的运动状态。
虽然月亮驴子不得不服从于缰绳的意志,但是这不是月亮驴子的本性。即使是这个时候,月亮驴子的本性也是不变的,他有做匀速直线运动的欲望。可见,惯性就是倔驴的“倔脾气”,跟外力没有关系。一旦缰绳没有了,所有的力都撤销,或者抵消,月亮驴子必将显露出其本身固有的属性,做匀速直线运动或者静止,这就是牛顿第一定律。
根据等效原理,如果我们定义“自由落体惯性系”,那么我们就可以不把引力看成是力,而是几何。也就是说,所有关于引力的信息都可以用时空的弯曲来描述。时空可以对应在一张全息屏上,这大概就是全息原理吧
熵力,逗你玩
||
料想Erik Verlinder看不懂中文,所以将题目写的好玩一点吧。事实上,博主根本没有资格评论Erik Verlinder同学的文章。这篇文章在10年和11年红的发紫,尤其在中国。我这人反应慢在大学同学里是出了名的。这里有一段小故事就不必讲了。总而言之,当时没兴趣,现在有兴趣了,找出来研究一把。
Erik Verlinder同学的文章严谨但不古板,最后还以大家喜闻乐见的方式结尾,皆大欢喜。内行看门道,外行看热闹,所以很多人喜欢看热闹,这个Erik Verlinder同学是知道的。热闹是什么?最热闹的事情莫过于打架。大街上如果有人打架,立马会围过来一圈人。当然有拉架的,有煽风点火的,更多的是看热闹的。如果你问他,您干什么的?答案是:"打酱油的!"文章的结尾提到牛顿和胡克打架。据说和牛顿打架的人很多,我想大概是因为牛顿自恃武功天下第一,横行乡里,引起很多人不服,前来挑战。Erik Verlinder同学最后一句话有点“数风流人物,还看今朝”的意思,可谓是霸气外漏。
熵力的基本假设是全息原理和等效原理,其中等效原理在这篇博文里讲的很详细,而全息原理俺不懂,想当然的以为就跟全息照相类似吧(亲爱的读者,您觉得呢?)。根据等效原理,如果我们定义“自由落体惯性系”,那么我们就可以不把引力看成是力,而是几何。也就是说,所有关于引力的信息都可以用时空的弯曲来描述。时空可以对应在一张全息屏上,这大概就是全息原理吧。过几天有空研究研究这个事情,亲爱的读者您如果知道,望不吝赐教。全息屏上可以定义熵,熵的变化描述时空的变化,而时空的变化描述引力,所以熵可以描述引力。Erik Verlinder做的事情是将这其中的曲折展示给大家看,推导出牛顿的引力公式和爱因斯坦方程。这里科普下,该文研究的是引力,说引力可以用熵来描写,没有其他三种作用力什么事儿。亲爱的读者,您可别把他们牵扯进来,以防打架。比如说摩擦力是电磁力,跟熵力不搭嘎。如果您是中学生,那您必然很熟悉胡克定律。一提到胡克,您脑海中就浮现出一根弹簧,胡克说弹力和其伸长量成正比。这里有一点小小的误会,您所想的那个弹力也是电磁力,别牵扯进来。
个人觉得熵力靠谱(不是不评论吗?)。孤立系熵不减,而引力没有排斥力,二者本应该有渊源。还有一个非常重要物理量也是单向变化的,您知道她是谁吗?这里您能得到什么启示?

这是什么车?
http://blog.sciencenet.cn/blog-441981-770672.html
Erik Verlinder同学的文章严谨但不古板,最后还以大家喜闻乐见的方式结尾,皆大欢喜。内行看门道,外行看热闹,所以很多人喜欢看热闹,这个Erik Verlinder同学是知道的。热闹是什么?最热闹的事情莫过于打架。大街上如果有人打架,立马会围过来一圈人。当然有拉架的,有煽风点火的,更多的是看热闹的。如果你问他,您干什么的?答案是:"打酱油的!"文章的结尾提到牛顿和胡克打架。据说和牛顿打架的人很多,我想大概是因为牛顿自恃武功天下第一,横行乡里,引起很多人不服,前来挑战。Erik Verlinder同学最后一句话有点“数风流人物,还看今朝”的意思,可谓是霸气外漏。
熵力的基本假设是全息原理和等效原理,其中等效原理在这篇博文里讲的很详细,而全息原理俺不懂,想当然的以为就跟全息照相类似吧(亲爱的读者,您觉得呢?)。根据等效原理,如果我们定义“自由落体惯性系”,那么我们就可以不把引力看成是力,而是几何。也就是说,所有关于引力的信息都可以用时空的弯曲来描述。时空可以对应在一张全息屏上,这大概就是全息原理吧。过几天有空研究研究这个事情,亲爱的读者您如果知道,望不吝赐教。全息屏上可以定义熵,熵的变化描述时空的变化,而时空的变化描述引力,所以熵可以描述引力。Erik Verlinder做的事情是将这其中的曲折展示给大家看,推导出牛顿的引力公式和爱因斯坦方程。这里科普下,该文研究的是引力,说引力可以用熵来描写,没有其他三种作用力什么事儿。亲爱的读者,您可别把他们牵扯进来,以防打架。比如说摩擦力是电磁力,跟熵力不搭嘎。如果您是中学生,那您必然很熟悉胡克定律。一提到胡克,您脑海中就浮现出一根弹簧,胡克说弹力和其伸长量成正比。这里有一点小小的误会,您所想的那个弹力也是电磁力,别牵扯进来。
个人觉得熵力靠谱(不是不评论吗?)。孤立系熵不减,而引力没有排斥力,二者本应该有渊源。还有一个非常重要物理量也是单向变化的,您知道她是谁吗?这里您能得到什么启示?

这是什么车?
http://blog.sciencenet.cn/blog-441981-770672.html
新熵力图像
从上学期开始,我一直想用引力即熵力理论找到暗能量的具体形式(当然私心是找到支持全息暗能量的证据),我们没有成功,似乎没有任何人成功了。
一开始,我就觉得Verlinde的想法中闭合的全息屏是最大的障碍,因为要研究宇宙学,不存在任何整体的Killing 矢量,特别是某种宇宙学视界上不存在整体Killing矢量,所以他的想法很难用到宇宙学上。
所以,我想到研究一个任意小的、开放的holographic screen。一个开放的全息屏当然不包含任何空间和物质,所以无法直接研究能量,但可以研究某段时间流过屏的能量。我们摸索了很长时间,后来我建议苗荣欣同学将Jacobson的原始做法移植到一个time-like全息屏上。
从7月份一直折腾到上个月,我们似乎看到了希望。开学后,谷伟也加入了我们。昨天,我将最后结果贴出来了:
A New Entropic Force Scenario and Holographic Thermodynamics
这个project一共做了四个月左右,终于结束了。
昨天在南宁的The first international workshop on the LHC era physics (LHEP2010) 上,我已经做了这个工作的演讲。
如果用一句话总结我们的建议与Verlinde的不同,就是,我们建议用Brown-York能量做全息屏上的能量,而不是Tolman-Komar质量,Verlinde假设后者满足能量均分定理(通过爱因斯坦方程,这个假设是正确的),而Brown-York能量一般不满足能量均分。
更一般的,我们从屏上的surface stress tensor出发。这个surface stress tensor含有面能量密度以及面压强信息,所以,我们还多了一个数据,就是压强。这个面stress tensor正比于面在时空中的extrinsic curvature。在Verlinde的图像中,面上只有温度,温度也是由几何给出的。我们的建议虽然不同,但在用到几何上面,与Verlinde并无本质不同。
我们建议的能量有如下的形式:
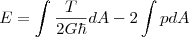
我们看到,非零的面压强破坏了能量均分。
推导爱因斯坦方程的大致过程是,从能量出发
![]()
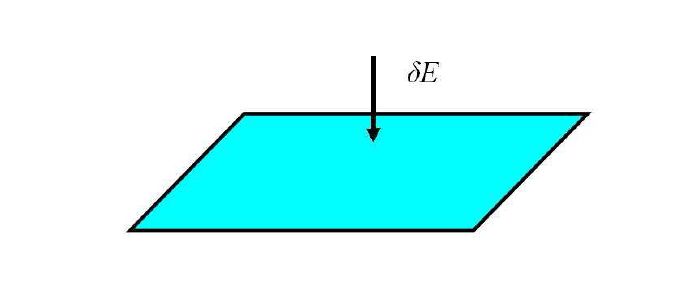
这个能流发生在时空中,根据全息原理,应该等于屏上的能量变化,而屏上的能量变化分两部分,一部分是面密度的变化,另一部分是能量从屏流到屏的其他部分,具体公式就不写了,图示如下:
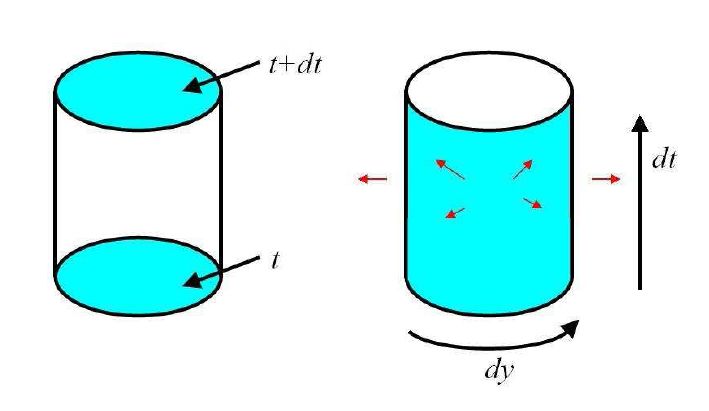
将两个能量变化相等,就能推出爱因斯坦方程。我们的推导比Verlinde的推导“完美”。第一,开放的屏可以任意小,所以积分方程可以变成微分方程。第二,Verlinde需要温度,而对于任意封闭的面,温度不是恒正定的。第三,既然我们需要用到面上的stress tensor而不是温度,我们可以用别的量取代extrinsic curvature,从而获得其他理论如高阶导数理论。过去我和庞毅证明了,Verlinde理论不能用到高导数理论。
我们的推导与Jacobson相似,他也用了能流,但他的全息屏是类光的,我们的是类时的。他只用到类光屏的面积变化(即熵变化),我们没有引进热力学。但后来我们可以引进热力学,采用Verlinde温度,但熵不由几何直接给出,需要解热力学第一定律。换言之,我们对爱因斯坦方程的推导还不能看成是热力学第一定律的应用。另外,类光屏上压强为零,也没有能量从屏流到屏的另一部分现象(所以热力学很简单,任意小的开放类光屏类似一个封闭系统)。
热力学需要单独研究,引进Verlinde温度,以及面压强,甚至化学势(事后看,这是自然的,面的变化自然会导致被激发的自由度的变化),我们研究了一个球对称气体,获得了全息熵。这个全息熵很像Bekenstein熵界,但对于不同的气体具体数值不同。全息熵远远大于气体的统计熵,说明全息屏上带有更多的信息。虽然我们的全息熵公式里有一个未定常数,这个结果是我们的图像的预言,而Verlinde图像还没有预言。
气体全息熵的导出是我相信这个新建议的主要原因。
全息熵中的未定常数是我们下一步的研究目标。我们现在同时在做三个相关的研究计划。
另外,很重要的是,Verlinde图像无法用到热力学上,对于一个气体,很难获得可以接受的熵公式。
我建议大家读我们的文章。
当然,不用说,还有很多要做的研究。
一开始,我就觉得Verlinde的想法中闭合的全息屏是最大的障碍,因为要研究宇宙学,不存在任何整体的Killing 矢量,特别是某种宇宙学视界上不存在整体Killing矢量,所以他的想法很难用到宇宙学上。
所以,我想到研究一个任意小的、开放的holographic screen。一个开放的全息屏当然不包含任何空间和物质,所以无法直接研究能量,但可以研究某段时间流过屏的能量。我们摸索了很长时间,后来我建议苗荣欣同学将Jacobson的原始做法移植到一个time-like全息屏上。
从7月份一直折腾到上个月,我们似乎看到了希望。开学后,谷伟也加入了我们。昨天,我将最后结果贴出来了:
A New Entropic Force Scenario and Holographic Thermodynamics
这个project一共做了四个月左右,终于结束了。
昨天在南宁的The first international workshop on the LHC era physics (LHEP2010) 上,我已经做了这个工作的演讲。
如果用一句话总结我们的建议与Verlinde的不同,就是,我们建议用Brown-York能量做全息屏上的能量,而不是Tolman-Komar质量,Verlinde假设后者满足能量均分定理(通过爱因斯坦方程,这个假设是正确的),而Brown-York能量一般不满足能量均分。
更一般的,我们从屏上的surface stress tensor出发。这个surface stress tensor含有面能量密度以及面压强信息,所以,我们还多了一个数据,就是压强。这个面stress tensor正比于面在时空中的extrinsic curvature。在Verlinde的图像中,面上只有温度,温度也是由几何给出的。我们的建议虽然不同,但在用到几何上面,与Verlinde并无本质不同。
我们建议的能量有如下的形式:
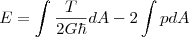
我们看到,非零的面压强破坏了能量均分。
推导爱因斯坦方程的大致过程是,从能量出发

这个能流发生在时空中,根据全息原理,应该等于屏上的能量变化,而屏上的能量变化分两部分,一部分是面密度的变化,另一部分是能量从屏流到屏的其他部分,具体公式就不写了,图示如下:

将两个能量变化相等,就能推出爱因斯坦方程。我们的推导比Verlinde的推导“完美”。第一,开放的屏可以任意小,所以积分方程可以变成微分方程。第二,Verlinde需要温度,而对于任意封闭的面,温度不是恒正定的。第三,既然我们需要用到面上的stress tensor而不是温度,我们可以用别的量取代extrinsic curvature,从而获得其他理论如高阶导数理论。过去我和庞毅证明了,Verlinde理论不能用到高导数理论。
我们的推导与Jacobson相似,他也用了能流,但他的全息屏是类光的,我们的是类时的。他只用到类光屏的面积变化(即熵变化),我们没有引进热力学。但后来我们可以引进热力学,采用Verlinde温度,但熵不由几何直接给出,需要解热力学第一定律。换言之,我们对爱因斯坦方程的推导还不能看成是热力学第一定律的应用。另外,类光屏上压强为零,也没有能量从屏流到屏的另一部分现象(所以热力学很简单,任意小的开放类光屏类似一个封闭系统)。
热力学需要单独研究,引进Verlinde温度,以及面压强,甚至化学势(事后看,这是自然的,面的变化自然会导致被激发的自由度的变化),我们研究了一个球对称气体,获得了全息熵。这个全息熵很像Bekenstein熵界,但对于不同的气体具体数值不同。全息熵远远大于气体的统计熵,说明全息屏上带有更多的信息。虽然我们的全息熵公式里有一个未定常数,这个结果是我们的图像的预言,而Verlinde图像还没有预言。
气体全息熵的导出是我相信这个新建议的主要原因。
全息熵中的未定常数是我们下一步的研究目标。我们现在同时在做三个相关的研究计划。
另外,很重要的是,Verlinde图像无法用到热力学上,对于一个气体,很难获得可以接受的熵公式。
我建议大家读我们的文章。
当然,不用说,还有很多要做的研究。
No comments:
Post a Comment