冪定律- 維基百科，自由的百科全書 - Wikipedia
zh.wikipedia.org/zh-hk/冪定律
缺少字詞： 衰减
平方反比定律_百度百科
baike.baidu.com/view/474387.htm
轉為繁體網頁
轉為繁體網頁
缺少字詞： 幂
Patent CN102301149B - 润滑条件监测- Google Patents
www.google.com/patents/CN102301149B?cl=zh - 轉為繁體網頁
预测城市人群移动量的人口权重机会模型 - 科学网—博客
blog.sciencenet.cn/blog-404069-822520.html
轉為繁體網頁
轉為繁體網頁
学渣请教：诺兰的高维空间中怎么旅行 - 豆瓣
www.douban.com/group/topic/67232410/
轉為繁體網頁
轉為繁體網頁
中国股市多标度的幂律分布与相关性关联研究_CNKI学问
xuewen.cnki.net/CJFD-GCXT200703001.html
轉為繁體網頁
轉為繁體網頁
普通物理的一些注记（1）：静电场和电介质- Sherry Lixue Cheng
www.sherrylixuecheng.com/9/post/2012/10/1.html
轉為繁體網頁
轉為繁體網頁
Bo Zhang's Homepage » 说说幂律谱的问题
bzhang.lamost.org/website/archives/power_law_spectrum/
轉為繁體網頁
轉為繁體網頁
缺少字詞： 衰减
phymath999: "輻射衰減距離平方反比",静电场随源区距离的3 ...
phymath999.blogspot.com/2012/10/3.html
轉為繁體網頁
轉為繁體網頁
[PDF]经验数字 - 中国计算机学会
www.ccf.org.cn/resources/1190201776262/2013/.../14.pd...
轉為繁體網頁
轉為繁體網頁
说说幂律谱的问题
在天文学中，幂律谱可以说是再常见不过了。非热辐射、宇宙线粒子能量分布，甚至还有陨星的质量分布，通通可以用幂律谱来描述。一般在统计工作中，也往往采用幂律形式来描述两个量之间的关系。由于本人正在计算非热辐射，最近基本上是每天都要与幂律谱打交道。
幂律谱的表示形式很简单，只是以下式子：
 \propto x^{-\alpha})
其中的
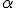唤作谱指数。其几何意义就是在对数坐标图上，谱的斜率为
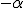。谱拟合也很简单，原则上说只要给定两点的
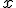与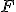
就可以做到。当然在实际操作中，由于测量误差等因素的存在，往往用的是多点拟合的方式。
当然从表达式来看，幂律就是个非常普遍的存在，线性关系可以看作是其中的一个特例。而人们熟知的平方反比定律也可以算作是幂律关系，描述黑体辐射能流密度与温度联系的斯忒藩—玻尔兹曼定律亦是如此。
天体物理学中，在电磁波谱的两端，幂律谱都在大唱主角，比如用于描述伽玛暴的Band双幂律谱，还有超新星遗迹在射电波段的辐射形式。对于后者，谱指数往往还是遗迹分类的重要因素：依靠中心致密天体供能的实心型往往谱指数偏小，作为激波产物的壳层型则偏大。
要说这幂律谱形的起源，首先要说说带电粒子能量（因此也就是洛伦兹因子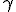
，因能量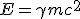
）的幂律分布。这样的粒子是加速的产物，常见的加速机制包括激波的一阶加速、磁场中的二阶费米加速等等，这里的阶数是针对能量的改变与粒子同加速区相对速度之间的关系而言的，一阶加速的效率要更高一些。
设每次加速后粒子的能量就增加到原先的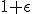
倍，同时有
的概率继续停留在加速区被进一步加速。那么它就有^n)
的概率来接受n次加速，而加速后粒子能量是原先的^n)
倍。由此得到的粒子集体能量分布就是幂律形式的，而且在
与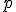
不太大的情况下，还可以导出幂律指数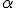近似满足
。
不同的指数意味着不同的加速机制。典型的例子就是初级宇宙线的能谱：
对于非热辐射机制，在天体物理学环境下一般是同步加速辐射与逆康普顿散射。将幂律分布的电子代入辐射的表达式，自然就可以给出幂律形式的谱形，而且对于同步加速辐射来说，若不考虑同步自吸收与冷却效应，电子的幂律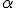指数与谱指数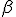
之间就应该有
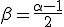的联系。当然如果冷却或者自吸收存在，问题要复杂许多。就算不考虑这些，很多精细的数值模型给出的激波加速电子谱分布往往也偏离单纯的幂律，因此实际的辐射谱会更加复杂。
至于其他呈幂律形态的统计关系，各自有各自的原因，如旋涡星系的Tully-Fisher关系可以用运动来解释，而椭圆星系的Faber-Jackson关系则可以归结为位力定理。描述伽玛暴的数种统计关系往往认为是同步辐射所致，对于流星体的质量分布，甚至还有说法认为是由于间接测量导致的假象。
幂律谱的表示形式很简单，只是以下式子：
当然从表达式来看，幂律就是个非常普遍的存在，线性关系可以看作是其中的一个特例。而人们熟知的平方反比定律也可以算作是幂律关系，描述黑体辐射能流密度与温度联系的斯忒藩—玻尔兹曼定律亦是如此。
天体物理学中，在电磁波谱的两端，幂律谱都在大唱主角，比如用于描述伽玛暴的Band双幂律谱，还有超新星遗迹在射电波段的辐射形式。对于后者，谱指数往往还是遗迹分类的重要因素：依靠中心致密天体供能的实心型往往谱指数偏小，作为激波产物的壳层型则偏大。
要说这幂律谱形的起源，首先要说说带电粒子能量（因此也就是洛伦兹因子
设每次加速后粒子的能量就增加到原先的
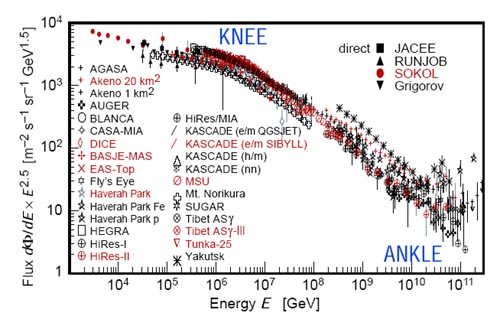
不同的指数意味着不同的加速机制。典型的例子就是初级宇宙线的能谱：
Hoerandel 2003
图中分别位于106与1010 GeV的两个拐点叫做“Knee”与“Ankle”，后者标志着河外起源的高能带电粒子，一般认为它们往往由活动星系核或是致密星双星系统加速。而关于前者的成因有多种说法，包括高能粒子从银河系中的逃逸，或者是达到超新星加速上限后，新的加速机制起了主导作用。对于非热辐射机制，在天体物理学环境下一般是同步加速辐射与逆康普顿散射。将幂律分布的电子代入辐射的表达式，自然就可以给出幂律形式的谱形，而且对于同步加速辐射来说，若不考虑同步自吸收与冷却效应，电子的幂律指数
至于其他呈幂律形态的统计关系，各自有各自的原因，如旋涡星系的Tully-Fisher关系可以用运动来解释，而椭圆星系的Faber-Jackson关系则可以归结为位力定理。描述伽玛暴的数种统计关系往往认为是同步辐射所致，对于流星体的质量分布，甚至还有说法认为是由于间接测量导致的假象。
推荐两篇进化生物学的paper－集智俱乐部
www.swarma.org/swarma/detail.php?id=17994
轉為繁體網頁
the power law 在天文学分类中的翻译结果 --cnki翻译助手
dict.cnki.net/h_51230402007.html - 轉為繁體網頁
爆发的评论(57) - 豆瓣读书
book.douban.com/subject/10769712/reviews
轉為繁體網頁
为什么我国的概率与统计学教科书里不怎么讲幂律分布 ... - 知乎
www.zhihu.com/question/20313934
轉為繁體網頁
高斯与天鹅| 日志| 果壳网科技有意思
www.guokr.com/blog/772814/
轉為繁體網頁
查看首页的源代码- 经济物理Wiki
econophysics.fudan.edu.cn/mwiki/index.php?title=首页...
轉為繁體網頁
金融物理學- MBA智库百科
wiki.mbalib.com/zh-tw/金融物理学
No comments:
Post a Comment