x的奇幻之旅_第11章函数:你能把一张纸对折8次以上吗?(2 ...
book.mihua.net › 科技工程 › x的奇幻之旅 - 轉為繁體網頁
數學科詞彙表
www.cmi.hku.hk/ref/glossary/mat/p.htm
耦合常數[编辑]
维基百科,自由的百科全书
在物理学中,耦合常數决定了相互作用的強度。例如在牛顿万有引力定律和爱因斯坦的广义相对论中,牛顿常数  就是引力的耦合常数。在粒子物理中,耦合常数的数值常常通过精细结构常数来给出。例如电磁相互作用的精细结构常数为
就是引力的耦合常数。在粒子物理中,耦合常数的数值常常通过精细结构常数来给出。例如电磁相互作用的精细结构常数为  , 其中
, 其中 是电磁相互作用的耦合常数,它正比与电子电荷
是电磁相互作用的耦合常数,它正比与电子电荷 。在日常使用时,耦合常数也经常和精细结构常数换用。
。在日常使用时,耦合常数也经常和精细结构常数换用。
在拉格朗日系统中,拉格朗日量或哈密顿量可以分成动能部分和相互作用部分。耦合常数决定了决定了相互作用部分相对于动能部分的强度。在存在多种相互作用的情况下,耦合常数也决定着各个相互作用的相对强度。
在经典力学中,耦合常数的大小可以通过测量力的大小直接得到。历史上牛顿常数是在牛顿死后71年后才由卡文迪什通过扭秤实验测量得到。但在量子力学中由于量子涨落的存在,出现在拉格朗日量或哈密顿量中的耦合常数是无法直接通过测量得到的。而实验中测量得到的耦合常数会随着探测尺度的不同而不同,被称为跑动的耦合常数。相应的,拉格朗日量中的耦合常数被称为裸耦合常数。
如果一个物理系统的相互作用的耦合常数比较小,则它的解可以通过微扰论近似得到。微扰论在量子场论的计算中尤其重要。
 远小于单位一,则其称为“弱耦合”的,此时问题的解
远小于单位一,则其称为“弱耦合”的,此时问题的解 可以按照
可以按照 的幂次(又叫做阶数)展开表示为,
的幂次(又叫做阶数)展开表示为,
 为没有相互作用时问题的解。这种方法称为微扰论。在上述微扰展开中,越高阶项的贡献越小。因而可以在适当阶做截断,以满足给定的精度要求。微扰论只有在弱耦合时才有用,因为若耦合常数
为没有相互作用时问题的解。这种方法称为微扰论。在上述微扰展开中,越高阶项的贡献越小。因而可以在适当阶做截断,以满足给定的精度要求。微扰论只有在弱耦合时才有用,因为若耦合常数 大于一,则越高阶项的贡献越大,任何有限阶数的截断都会带来严重的误差。
大于一,则越高阶项的贡献越大,任何有限阶数的截断都会带来严重的误差。
微扰论在量子场论中具有核心地位。量子场论中的微扰论计算一般是通过费曼图和费曼规则来系统地组织实现的,因为费曼图就是按照耦合常数的幂次画出来的。电磁相互作用、弱相互作用在寻常尺度下都是弱耦合的相互作用。而强相互作用在短距离上(尺度远小于飞米时)也是弱耦合的。
 来理解。测量使用的能量越高,测量仪器能够分辨的尺度就越小。在小尺度下,将能看到更多的虚粒子的涨落。这种效应与电荷在介质中的极化效应是相似的。因而也被称为真空极化。这种随着能标的改变而改变的“耦合常数”被称为跑动的耦合常数。
来理解。测量使用的能量越高,测量仪器能够分辨的尺度就越小。在小尺度下,将能看到更多的虚粒子的涨落。这种效应与电荷在介质中的极化效应是相似的。因而也被称为真空极化。这种随着能标的改变而改变的“耦合常数”被称为跑动的耦合常数。
β函數β(g) 描述了耦合常数随能量标度μ變化的的情形,其定義如下
若量子场论中的β函數為零,則此理論為共形場論。若在高能量下β函数为正,代表耦合常数随着能标的增加而增加;若在高能量下β函数为负,则代表耦合常数随着能标的增加减小,这种现象叫做漸近自由。
 為一常數,
為一常數, 是夸克味的数目。这是最先由韦尔切克、波利策和格娄斯計算的。
是夸克味的数目。这是最先由韦尔切克、波利策和格娄斯計算的。
相反的,耦合程度會隨著能量降低而增強,因此在低能量時耦合效應會變強。尤其是在能标Λ上由微扰论定义耦合常数开始出现发散,因此不能用微擾效應來求解。Λ稱為QCD尺度,其數值為
間改善,而其數值需動態決定。
 就是引力的耦合常数。在粒子物理中,耦合常数的数值常常通过精细结构常数来给出。例如电磁相互作用的精细结构常数为
就是引力的耦合常数。在粒子物理中,耦合常数的数值常常通过精细结构常数来给出。例如电磁相互作用的精细结构常数为  , 其中
, 其中 是电磁相互作用的耦合常数,它正比与电子电荷
是电磁相互作用的耦合常数,它正比与电子电荷 。在日常使用时,耦合常数也经常和精细结构常数换用。
。在日常使用时,耦合常数也经常和精细结构常数换用。在拉格朗日系统中,拉格朗日量或哈密顿量可以分成动能部分和相互作用部分。耦合常数决定了决定了相互作用部分相对于动能部分的强度。在存在多种相互作用的情况下,耦合常数也决定着各个相互作用的相对强度。
在经典力学中,耦合常数的大小可以通过测量力的大小直接得到。历史上牛顿常数是在牛顿死后71年后才由卡文迪什通过扭秤实验测量得到。但在量子力学中由于量子涨落的存在,出现在拉格朗日量或哈密顿量中的耦合常数是无法直接通过测量得到的。而实验中测量得到的耦合常数会随着探测尺度的不同而不同,被称为跑动的耦合常数。相应的,拉格朗日量中的耦合常数被称为裸耦合常数。
如果一个物理系统的相互作用的耦合常数比较小,则它的解可以通过微扰论近似得到。微扰论在量子场论的计算中尤其重要。
基本相互作用[编辑]
强、弱、电磁和引力四种基本相互作用中的耦合常数的大小大致如下 [1]:| 相互作用 | 耦合常数 |
|---|---|
| 强相互作用 |  |
| 电磁相互作用 |  |
| 弱相互作用 |  |
| 引力相互作用 |  |
弱耦合与微扰论[编辑]
如果一个问题中的耦合常数 远小于单位一,则其称为“弱耦合”的,此时问题的解
远小于单位一,则其称为“弱耦合”的,此时问题的解 可以按照
可以按照 的幂次(又叫做阶数)展开表示为,
的幂次(又叫做阶数)展开表示为, 为没有相互作用时问题的解。这种方法称为微扰论。在上述微扰展开中,越高阶项的贡献越小。因而可以在适当阶做截断,以满足给定的精度要求。微扰论只有在弱耦合时才有用,因为若耦合常数
为没有相互作用时问题的解。这种方法称为微扰论。在上述微扰展开中,越高阶项的贡献越小。因而可以在适当阶做截断,以满足给定的精度要求。微扰论只有在弱耦合时才有用,因为若耦合常数 大于一,则越高阶项的贡献越大,任何有限阶数的截断都会带来严重的误差。
大于一,则越高阶项的贡献越大,任何有限阶数的截断都会带来严重的误差。微扰论在量子场论中具有核心地位。量子场论中的微扰论计算一般是通过费曼图和费曼规则来系统地组织实现的,因为费曼图就是按照耦合常数的幂次画出来的。电磁相互作用、弱相互作用在寻常尺度下都是弱耦合的相互作用。而强相互作用在短距离上(尺度远小于飞米时)也是弱耦合的。
跑动的耦合常数[编辑]
在量子力学尤其是量子场论中,由于量子涨落效应的存在,相互作用顶点被虚粒子所修正,成为非局域性的相互作用顶点。因此,测得的耦合常数的大小与原拉格朗日量或哈密顿量中的耦合常数不同,且与测量的能量标度有关。后一点可以通过不确定关系, 来理解。测量使用的能量越高,测量仪器能够分辨的尺度就越小。在小尺度下,将能看到更多的虚粒子的涨落。这种效应与电荷在介质中的极化效应是相似的。因而也被称为真空极化。这种随着能标的改变而改变的“耦合常数”被称为跑动的耦合常数。
来理解。测量使用的能量越高,测量仪器能够分辨的尺度就越小。在小尺度下,将能看到更多的虚粒子的涨落。这种效应与电荷在介质中的极化效应是相似的。因而也被称为真空极化。这种随着能标的改变而改变的“耦合常数”被称为跑动的耦合常数。β函數β(g) 描述了耦合常数随能量标度μ變化的的情形,其定義如下
若量子场论中的β函數為零,則此理論為共形場論。若在高能量下β函数为正,代表耦合常数随着能标的增加而增加;若在高能量下β函数为负,则代表耦合常数随着能标的增加减小,这种现象叫做漸近自由。
量子电动力学和朗道奇點[编辑]
根据微扰论,描写电磁相互作用的量子电动力学的β函數为正,耦合效應會隨著能量增加而增強。量子电动力学在高能量時會變得高度耦合,甚至在某些有限時能量下,耦合係數似乎會變成無限大,此現象最早是由列夫·达维多维奇·郎道所發現,因此稱為郎道奇點。不過微擾论在强耦合情况下已经失效。而且达到朗道奇点所需的能标远远超过普朗克能标,而一般认为量子场论在普朗克能标左右已经不再适用。量子色动力学和漸近自由[编辑]
弗朗克·韦尔切克、休·波利策及戴维·格娄斯發現,描写强相互作用的量子色动力学的β函數為负。因此量子色动力学的耦合在高能量時會降低。其發現者因此获得2004年的諾貝爾物理獎[2]。在一阶近似下耦合係數大致可以表示為下式: 為一常數,
為一常數, 是夸克味的数目。这是最先由韦尔切克、波利策和格娄斯計算的。
是夸克味的数目。这是最先由韦尔切克、波利策和格娄斯計算的。相反的,耦合程度會隨著能量降低而增強,因此在低能量時耦合效應會變強。尤其是在能标Λ上由微扰论定义耦合常数开始出现发散,因此不能用微擾效應來求解。Λ稱為QCD尺度,其數值為
弦理論[编辑]
弦理論下的耦合常數有明顯的不同點,弦理論的每一個微擾敘述和一個弦耦合常數有關,可是這些耦合常數不是事先定義、可調整及共適性的常數,而是動態的純量場,會依位置和時間改善,而其數值需動態決定。
x的奇幻之旅_第11章 函数:你能把一张纸对折8次以上吗?(2)
(畅游书海,品尝文化,陶冶情操,彰显智慧。米花在线书库为您营造舒适阅读环境而努力,希望书友继续支持。)
为什么这个函数的图像会呈弓形呢?因为有一把看不见的数学“镊子”正在悄悄地使劲。在这个关于y的方程中,x被“转化”成了x2,这种转化的工具就像日常生活中我们使用的镊子一样,能够对被转化物施加拉力,使被转化物弯曲。本来,我们的原材料可以看作x轴上的一小段线段,它是完全水平的,经过这个方程的转化,这一小段原材料的每一个点都受到了拉力的作用,就像被镊子夹起来一样,原材料被弯曲拉长了,形成了我们在上图中看到的弓形。
上面我们谈到的是方程中x2的部分,那么,y=4-x2中的这个常数4又起到了什么作用呢?同样用五金工具进行类比,这个常数4就好像把一幅画挂在墙上的那枚钉子一样。这枚钉子将拉开的弓形向上提起,固定在y轴上4的位置上。就像钉子不会改变弓的形状一样,常数4也不会改变函数的形状,它只是把这个图形的所有点都向上提高了4个单位而已,我们给这类“工具”起了一个统一的名字,叫作“常数函数”。game.mihua.net
上面的这个例子很好地诠释了函数的双重作用。一方面,函数和五金工具一样,是一种可以转化原材料的工具,x2能把x轴的一段拉伸变弯,而4则能把整个图形向上提。另一方面,函数又相当于工具所处理的原材料,4和–x2都是函数的零部件,它们共同组合成了一个更复杂的函数4–x2,就好像电线、电池、晶体管等零部件可以组成一台收音机一样。
当你了解了函数的双重作用,你就会发现生活中处处都有函数。上面的这个弓形或者说拱门形的东西,它的学名叫作“抛物线”。抛物线是平方函数的学名,生活中处处都能见到抛物线,也就意味着平方函数常常在我们周围出没。不管是喷泉形成的水柱,还是篮球运动的轨迹,都有二次函数的身影。如果你什么时候去美国的底特律国际机场转机,别忘了留几分钟时间逛逛达美航空的候机楼,那里的喷泉组是世界上最壮观的抛物线表演之一。
从抛物线和常数出发,我们可以推广得到一类更为广阔的函数:幂函数。幂函数的形式为xn。在幂函数中,未知数x被连乘n次,n是一个给定的已知数。比如,
对于抛物线函数来说,n=2;而对于常数函数来说,n=0。
只要改变n的值,我们就能得到一系列非常方便好用的数学工具。比如,一次函数(n=1)是一个斜坡,它可以很好地描述速率稳定的增长或是衰减的过程。一次函数又叫作线性函数,因为在xy平面上,一次函数的图像是一条直线。如果外面在下着一场速度均匀的雨,你把一个铁桶放在室外,那么桶内的积水量和时间的关系就是一种线性关系,这种关系可以用一次函数来表示。
另一个非常有用的工具是平方反比例函数,也就是n=-2所得到的幂函数。平方反比例函数可以很好地描述波或者力在三维空间中传播时的衰减情况。比如,要研究一个声音如何随着传播距离的变化而越变越轻,就要用到平方反比例函数。
在各行各业中,科学家们和工程师们都会大量运用幂函数,它们能够非常好地表达和描述相对平缓的增长或者衰减的过程
量子場論中的微擾論計算一般是通過費曼圖和費曼規則來系統地組織實現的,因為費
1 day ago - 量子场论中的微扰论计算一般是通过费曼图和费曼规则来系统地组织实现的,因为费
现在,特霍夫特证明,所有在大N 展开中贡献最大的费曼图都可以画在平面 ... 通常以阶乘方式发散的微扰论不同,当亏格数固定时,费曼图的个数只是以圈数的幂次增
用微扰论研究弦论,一开始就先天不足,如同用费曼图研究量子场论一样,我们在 .... 以阶乘方式发散的微扰论不同,当亏格数固定时,费曼图的个数只是以圈数的幂次 ...
用耦合常数的幂次来确定费曼图的阶数,哪个的阶数与其他不同? 15. 16. 17. 18. 查了不少量子力学和相对论(和标准答案),拿到了perfect end。 本文标签: 物理.
2013年9月16日 - 这是因为相空间体积元包含的粒子数宏观无限小,微观无限大。选1 14. 用耦合常数的幂次来确定费曼图的阶数,哪个的阶数与其他不同?
2011年7月9日 - 比如曾经用于描述弱相互作用的四费米子相互作用理论就是如此。量纲分析指出,当相互作用常数的量纲为质量量纲的零次幂的时候,费曼图阶数 ...
2014年5月31日 - ... 對應著一套圖形化的方法--對費曼圖進行積分拉氏量不僅對決定費曼圖的 ... 的零次冪的時候費曼圖階數增長不改變發散級次正次冪的時候高階圖 ...
舉的雙體非輕子衰變道為例,此過程可如圖一所示一分為二,下半部代表的躍遷形 ... 次要項,包括屬於高階(高冪次的耦合常數)修正的弱作用頂點圈圖的貢獻,如圖 .... 場及等效拉氏量,後者則是費因曼圖,SCET級數中的每一項皆有對應的費因曼圖。
为什么这个函数的图像会呈弓形呢?因为有一把看不见的数学“镊子”正在悄悄地使劲。在这个关于y的方程中,x被“转化”成了x2,这种转化的工具就像日常生活中我们使用的镊子一样,能够对被转化物施加拉力,使被转化物弯曲。本来,我们的原材料可以看作x轴上的一小段线段,它是完全水平的,经过这个方程的转化,这一小段原材料的每一个点都受到了拉力的作用,就像被镊子夹起来一样,原材料被弯曲拉长了,形成了我们在上图中看到的弓形。
上面我们谈到的是方程中x2的部分,那么,y=4-x2中的这个常数4又起到了什么作用呢?同样用五金工具进行类比,这个常数4就好像把一幅画挂在墙上的那枚钉子一样。这枚钉子将拉开的弓形向上提起,固定在y轴上4的位置上。就像钉子不会改变弓的形状一样,常数4也不会改变函数的形状,它只是把这个图形的所有点都向上提高了4个单位而已,我们给这类“工具”起了一个统一的名字,叫作“常数函数”。game.mihua.net
上面的这个例子很好地诠释了函数的双重作用。一方面,函数和五金工具一样,是一种可以转化原材料的工具,x2能把x轴的一段拉伸变弯,而4则能把整个图形向上提。另一方面,函数又相当于工具所处理的原材料,4和–x2都是函数的零部件,它们共同组合成了一个更复杂的函数4–x2,就好像电线、电池、晶体管等零部件可以组成一台收音机一样。
当你了解了函数的双重作用,你就会发现生活中处处都有函数。上面的这个弓形或者说拱门形的东西,它的学名叫作“抛物线”。抛物线是平方函数的学名,生活中处处都能见到抛物线,也就意味着平方函数常常在我们周围出没。不管是喷泉形成的水柱,还是篮球运动的轨迹,都有二次函数的身影。如果你什么时候去美国的底特律国际机场转机,别忘了留几分钟时间逛逛达美航空的候机楼,那里的喷泉组是世界上最壮观的抛物线表演之一。
从抛物线和常数出发,我们可以推广得到一类更为广阔的函数:幂函数。幂函数的形式为xn。在幂函数中,未知数x被连乘n次,n是一个给定的已知数。比如,
对于抛物线函数来说,n=2;而对于常数函数来说,n=0。
只要改变n的值,我们就能得到一系列非常方便好用的数学工具。比如,一次函数(n=1)是一个斜坡,它可以很好地描述速率稳定的增长或是衰减的过程。一次函数又叫作线性函数,因为在xy平面上,一次函数的图像是一条直线。如果外面在下着一场速度均匀的雨,你把一个铁桶放在室外,那么桶内的积水量和时间的关系就是一种线性关系,这种关系可以用一次函数来表示。
另一个非常有用的工具是平方反比例函数,也就是n=-2所得到的幂函数。平方反比例函数可以很好地描述波或者力在三维空间中传播时的衰减情况。比如,要研究一个声音如何随着传播距离的变化而越变越轻,就要用到平方反比例函数。
在各行各业中,科学家们和工程师们都会大量运用幂函数,它们能够非常好地表达和描述相对平缓的增长或者衰减的过程
耦合常數- 維基百科,自由的百科全書 - Wikipedia
zh.wikipedia.org/zh-hk/耦合常數
phymath999: 费曼图就是按照耦合常数的幂次画出来的, 耦合 ...
phymath999.blogspot.com/2014/12/blog-post_669.html
轉為繁體網頁
回复:弦论通俗演义zt_相对论吧_百度贴吧
tieba.baidu.com/p/319161318?pn=3
轉為繁體網頁
弦论通俗演义(二十) - 饮水思源
https://bbs.sjtu.edu.cn/bbsanc,path,%2Fgroups%2FGROUP...
轉為繁體網頁
withinbeyond的日记 - 豆瓣
www.douban.com/people/withinbeyond/notes
轉為繁體網頁
臣妾已经再起不能了(终章三) - 豆瓣
www.douban.com/note/302943173/
轉為繁體網頁
音乐快递:高阶导数项的能量(量纲) 幂次较高, 相应的耦合 ...
bbs.wenxuecity.com › 论坛 › 音乐快递
轉為繁體網頁
重整化- 知識Wiki - 知網
www.labtud.com/article-3048329-1.html
[DOC]DOC檔
psroc.phys.ntu.edu.tw/bimonth/download.php?d=2&cpid=135...

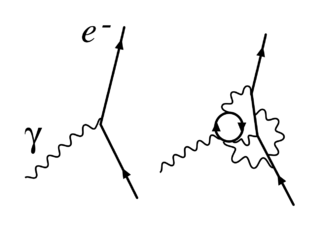


 阶的强相互作用的耦合常数随着能标的变化
阶的强相互作用的耦合常数随着能标的变化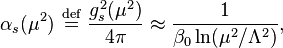
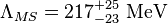
No comments:
Post a Comment