phymath999: Delta Function Model of a Molecule attractive delta function potential and look for the bound states. Putting k in the formula for \bgroup\color{black}$\kappa$\egroup in terms of the energy.

Tuesday, December 2, 2014

Delta Function Model of a Molecule attractive delta function potential and look for the bound states. Putting k in the formula for \bgroup\color{black}$\kappa$\egroup in terms of the energy.

http://quantummechanics.ucsd.edu/ph130a/130_notes/node154.htmlPutting in the formula for $\bgroup\color{black}$\kappa$\egroup$ in terms of the energy.

$\epsfig{file=figs/potdelta.eps,width=5in}$
We now need to meet the boundary condition on the first derivative at $\bgroup\color{black}$x=0$\egroup$ . Recall that the delta function causes a known discontinuity in the first derivative.

The Delta Function Model of a Molecule *
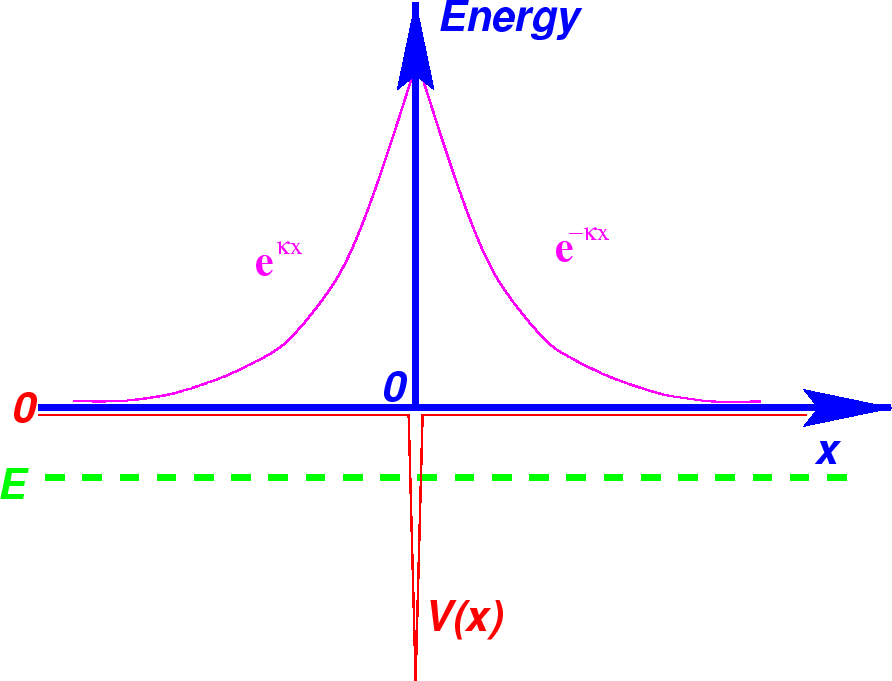
The use of two delta functions allows us to see, to some extent, how atoms bind into molecules. Our potential is

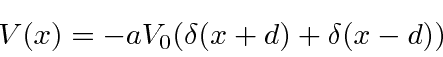
$\begin{displaymath}\bgroup\color{black} V(x)=-aV_0(\delta(x+d)+\delta(x-d)) \egroup\end{displaymath}$

with attractive delta functions at 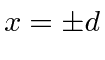$\bgroup\color{black}$x=\pm d$\egroup$ . This is a parity symmetric potential, so we can assume that our solutions will be parity eigenstates.
For even parity, our solution in the three regions is

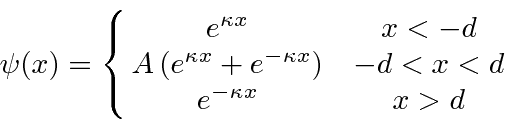
$\begin{displaymath}\bgroup\color{black} \psi(x)=\left\{ \matrix{e^{\kappa x} & x... ...x}\right) & -d<x<d\cr e^{-\kappa x} & x>d\cr} \right. \egroup\end{displaymath}$

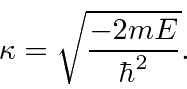
$\begin{displaymath}\bgroup\color{black} \kappa=\sqrt{-2mE\over\hbar^2} .\egroup\end{displaymath}$

Since the solution is designed to be symmetric about $\bgroup\color{black}$x=0$\egroup$ , the boundary conditions at $\bgroup\color{black}$-d$\egroup$ are the same as at $\bgroup\color{black}$d$\egroup$ . The boundary conditions determine the constant $\bgroup\color{black}$A$\egroup$ and constrain $\bgroup\color{black}$\kappa$\egroup$ .
A little calculation gives

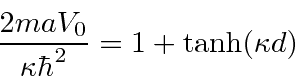
$\begin{displaymath}\bgroup\color{black} {2maV_0\over\kappa\hbar^2}=1+\tanh(\kappa d) \egroup\end{displaymath}$

This is a transcendental equation, but we can limit the energy.

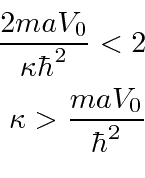
$\begin{eqnarray*} {2maV_0\over\kappa\hbar^2}<2 \\ \kappa > {maV_0\over \hbar^2} \\ \end{eqnarray*}$

Since 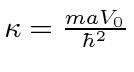$\bgroup\color{black}$\kappa={maV_0\over\hbar^2}$\egroup$ for the single delta function, this 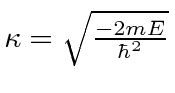$\bgroup\color{black}$\kappa=\sqrt{-2mE\over\hbar^2}$\egroup$ is larger than the one for the single delta function. This means that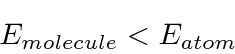 $\bgroup\color{black}$E$\egroup$ is more negative and there is more binding energy.

$\begin{displaymath}\bgroup\color{black} E_{molecule}<E_{atom} \egroup\end{displaymath}$

Basically, the electron doesn't have to be a localized with two atoms as it does with just one. This allows the kinetic energy to be lower.
The figure below shows the two solutions plotted on the same graph as the potential.

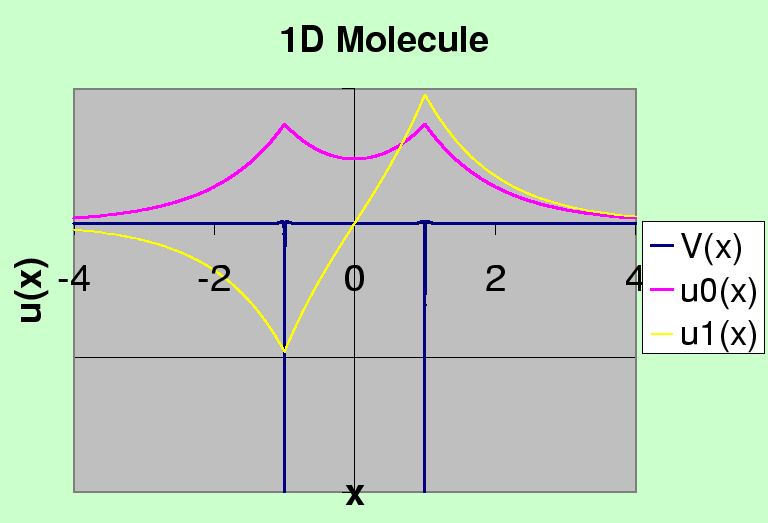
$\epsfig{file=figs/mol1d.eps,width=5in}$

Two Hydrogen atoms bind together to form a molecule with a separation of 0.74 Angstroms, just larger than the Bohr radius of 0.53 Angstroms. The binding energy (for the two electrons) is about 4.5 eV. If we approximate the Coulomb potential by with a delta function, setting 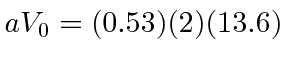$\bgroup\color{black}$aV_0=(0.53)(2)(13.6)$\egroup$ eV Angstroms, our very naive calculation would give 1.48 eV for one electron, which is at least the right order of magnitude. The odd parity solution has an energy that satisfies the equation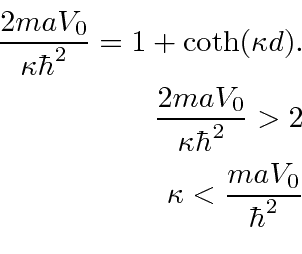

$\begin{eqnarray*} {2maV_0\over\kappa\hbar^2} = 1+\coth(\kappa d) .\\ {2maV_0\over\kappa\hbar^2}>2 \\ \kappa < {maV_0\over \hbar^2} \\ \end{eqnarray*}$

This energy is larger than for one delta function. This state would be called anti-bonding.

phymath999

Tuesday, December 2, 2014

Delta Function Model of a Molecule attractive delta function potential and look for the bound states. Putting k in the formula for \bgroup\color{black}$\kappa$\egroup in terms of the energy.

No comments:

Post a Comment