普朗克的黑體輻射定律[60]。他成功地將一個諧振腔內的電磁場分解成其傅立葉模式，並假設了每一種模式的能量都是E=h\nu\,的整數倍，將這些模式求和就得到了黑體輻射定律

國立台灣師範大學物理系 物理教學示範實驗教室(舊網站) 物理問題討論區 (黃福坤) 我們也針對科學教學建立開課系統:科學園,讓老師更方便運用網路科技輔助教學，歡迎教師多加利用！ 中學物理(維基) (學習物理不只是know HOW 更重要的是 know WHY, 歡迎參考聞名全球的物理動畫, 英文網頁NTNUJAVA以動畫為主) 新聞 報導 與白話物理

關鍵詞 最近天 物理名詞中英檢索 無法登入或系統功能不正常回報

討論區首頁 >>物理課程相關問題(分成國中/高中/大學等區) >>日常生活中的物理現象>>請問光是否能轉換能量結構

IP=107.193.137.176;[訪客]光臨時間 2957 秒, 閱覽 2 頁 本區 註冊 且 登入 者方可留言

powered by 討論區

本討論串狀態為: 未定(請幫忙選擇)問題已經圓滿解決提出問題,等待討論討論進行中,尚未有結論問題爭辯中,還沒有定論

歡迎參考幾篇日常生活中的物理專文

光學 標題:請問光是否能轉換能量結構 1:黃胤龍榮譽點數1點 (大學)張貼:2012-01-03 13:37:58:地點*台灣基隆 守恆 波動 質量 粒子 能量 ,本留言獲[]給賞金共 1 點 剛剛在這討論版看到一篇文章再說有關於空間扭曲的說明 http://www.phy.ntnu.edu.tw/demolab/phpBB/viewtopic.php?topic=3194 上面有人寫到光在靜止的時候質量為零... 我就想到幾個問題好奇想問問看 1.光可以靜止嗎?... 如果光不傳遞光子或波動..怎麼實驗觀察光在原地靜止不動...是否最多只能假設時間趨近零吧...就算重力(或黑洞)影響光路徑...造成觀察上的變化..可觀察的結果是發現光就此一直在原地靜止不動呢?  還是相對觀察者而言近似於靜止不動? 2.光是有質量的?.. 就我上網查詢，光具有波動和粒子屬性，而光能被重力場影響，就我所知有關重力場的理論中能被重力影響的物質都是具有質量，所以光是有質量的? 3.光的能量型態是什麼? 一般的物質可以透過物理或化學的方式轉換成能量型態，例如:火柴可以燃燒變成火的能量型態，電燈泡發電可以變成光的能量型態，如果光有質量，根據質能守恆，光也能轉換成能量，那光的能量型態是什麼? 4.如果光有能量型態是否能轉換成特定能量結構存在? 因為目前的太陽能發電除了在太空中的衛星外，地表的太陽能發電都只能等天氣好的白天，天氣不好的時候或者夜晚都無法產生發電，若光可以轉換成特定能量結構儲存起來，就可以在晚上和天氣不好的時候發電，且若光的能量能加以儲存，也許能製造一種利用可儲存起來的光來行走的光電車，既減少因使用石油產生的汙染，且因為光是免費的，所以除了製造儲存光的成本和收集光設備成本以及人士和社會成本(稅等等..)以外，這種能量應該會非常廉價 PS我物理不好只有國中程度...大學也沒選修相關課程..現在是社會人士..單純只是有興趣想知道) 2:Hydrogen Dioxide(研究所)張貼:2012-05-06 13:22:40:地點*台灣高雄 [回應上一篇] 能量 波動 電磁波 質量 光是電磁波，所謂的波動，就與時間、空間有關。若是光靜止了，表示電和磁的變動在空間中定點來看的話與時間無關，你能講出來這是甚麼意義呢？ 依據愛因斯坦質能轉換關係式Ｅ＝ｍｃ２   ,  光有能量，所以光具有質量。 Ｅ＝ｍｃ２＝ｈｆ依據此關係式作轉換就可以得到光的質量了 3:Hydrogen Dioxide(研究所)張貼:2012-06-04 14:26:05:地點 台灣高雄 [回應第1篇] 電荷 能量 量子 質子 電子 頻率 帶電 質量 電磁波 粒子 位移 動量 動量守恆 守恆 相位 振幅 電場 輻射 磁場 相對論 Quote: 在 2012-01-03 13:37:58, 黃胤龍 寫了: 3.光的能量型態是什麼? 4.如果光有能量型態是否能轉換成特定能量結構存在? 光子 (量子場論) 光子與量子場論 [编辑] 二次量子化 主條目：量子場論 不同的「電磁波模式」 可以被認為是彼此獨立的諧振子，一個光子對應著該種模式的對應能量的最小單位 1910年，彼得·德拜從一個相對簡單的假設推導出了普朗克的黑體輻射定律[60]。他成功地將一個諧振腔內的電磁場分解成其傅立葉模式，並假設了每一種模式的能量都是的整數倍，將這些模式求和就得到了黑體輻射定律。不過，德拜的方法沒有能夠給出愛因斯坦於1909年得到的黑體輻射能量漲落公式的正確形式[8]。 1925年，波恩、海森堡和約當 (Pascual Jordan) 對德拜的概念做了關鍵性的重新闡述[61]。在古典理論中就可以證明，電磁場的傅立葉模式，這個由其波矢k和偏振態標記的平面電磁波的一組完備集合，和無耦合的諧振子的一組集合等價。在量子力學中，這組諧振子的能級可用表示，是諧振子的頻率。而下一個關鍵步驟就是證明電磁場的每一種傅立葉模式的能級都對應可用表示的具有n個光子的一個態，每一個光子的能量是。這種方法給出了正確的能量漲落公式。 在量子場論中，一個可觀測事件的機率來源於對所有可能過程的機率振幅（一個複數）求和。在這裡的費曼圖中，機率等於振幅之和的模的平方 狄拉克在此基礎上做了進一步推導[55][56]，他將一個電荷和電磁場的交互作用處理為引起光子能級躍遷的微擾，能級躍遷造成了光子數量的變化，但總體上系統滿足能量和動量守恆。狄拉克成功地從第一性原理導出了愛因斯坦係數和的形式，並證明了光子的玻色-愛因斯坦統計是電磁場量子化的自然結果（玻色的推導過程正好相反，他在假設玻色-愛因斯坦統計成立的條件下導出了普朗克公式）。在狄拉克的時代，人們還不知道包括光子之內的所有玻色子都服從玻色-愛因斯坦統計。 狄拉克的二階微擾理論會涉及到虛光子，虛光子可以認為是極短暫的電磁場的中間態，如靜電場或靜磁場中的交互作用就是由虛光子來傳遞。在量子場論中，可觀測事件的機率振幅是由對所有可能的中間態求和得到的，包括那些沒有物理意義的態。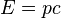這樣虛光子並沒有如這樣公式的約束，而且可能會存在兩個以外的偏振態，在某些規範條件下光子可能會有三個甚至四個偏振態。儘管虛光子不能被觀測到，它們對可觀測事件的機率的貢獻是可以測量到的。當然，二階微擾以及更高階的微擾在數學上會使求和的結果無限大，對於這種不存在物理意義的結果解決的技巧是重整化。其他種類的虛粒子也能夠對求和產生貢獻，例如在兩個光子的交互作用中的虛電子-正電子對。 在現代物理的符號系統中，電磁場的量子態是用一個福柯態來表示，這是每一種電磁場模式對應的量子態的張量積： 這裡表示的量子態意為有個光子處於模式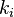下。在這種符號系統中，模式下產生一個新光子的過程被記做。這只是波恩、海森堡和約當的概念的一種數學表述，並沒有更多的物理內容。 [编辑] 光子：規範玻色子 主條目：規範場論 電磁場可用規範場論來理解為要求時空中每一個位置都滿足對稱性要求的結果[62]。對於電磁場，這種規範對稱性是複數的局域阿貝爾U(1)對稱性，複數代表著可以自由改變其相位，而不改變其實數部分，例如能量或拉格朗日量是複數的實部。 在對稱不破缺的前提下，阿貝爾規範場的量子必須是無質量的、不帶電荷的玻色子，因此理論預言光子為無質量無電荷並帶有整數自旋的粒子。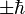電磁交互作用的形式決定了光子的自旋一定為±1，即Helicity一定為，對應著光子古典概念中的左旋和右旋；而虛光子也可能會具有無物理意義的其他自旋態[62]。物理學家一直在致力於檢查實驗結果和標準模型的預言相矛盾之處，特別是從實驗中計算光子所帶電荷和內秉質量的上限，任何一個值非零都是對標準模型致命的破壞。然而，目前為止所有實驗都證明光子具有的電荷和內秉質量為零[63][64][65][66][67][68][69][70][71][72][73] ，現今最為廣泛接受的上限值分別為5×10−52庫侖（3×10−33倍基本電荷）和1.1×10−52千克（6×10-17 電子伏特）[74]。 在流行的標準模型中，光子是電弱相互作用的四個規範玻色子之一，其他三個是參與弱交互作用的W+, W−和Z0，它們都具有內秉質量，因此需要一種SU(2)規範對稱破缺的機制來解釋。光子和W、Z玻色子的弱電統一理論是由格拉肖、薩拉姆和溫伯格完成的，三人因此項工作獲得1979年的諾貝爾物理學獎[75][76][77] 。而大統一理論的創立，是物理學家試圖將這四種規範玻色子和傳遞強交互作用的八種膠子規範玻色子聯繫起來的嘗試；然而大統一理論的一些關鍵性預言，例如質子的衰減，還沒有在實驗中得到證實。 [编辑] 光子的結構 參見：量子色動力學 所謂光子結構的測量，在量子色動力學中是指觀測光子場的量子漲落[78]，這種能量漲落用一個光子的結構方程式來描述。目前對光子結構的測量一般都依賴於對光子與電子，以及正負電子的對撞時的深度非線性散射的觀測[79]。根據量子色動力學，光子既能以無尺寸粒子，即輕子的方式參與交互作用；也能以一組夸克和膠子的集合體，即強子的方式參與。決定光子結構的並不是像質子那樣由傳統的價夸克分布，而是由輕子的漲落而形成的部分子的集合。 [编辑] 對系統質量的貢獻 當一個系統輻射出一個光子，從相對系統靜止的參考系來看，能量相應地降低了一個光子對應的能量，這造成系統質量降低了；同樣地，系統吸收光子時質量也會增加相應的值。 這一概念被應用於狄拉克發起的理論——量子電動力學（QED）的關鍵性預言中。QED有能力在很高的精確度上對輕子的磁偶極矩值作出預測，雖然這些預測將虛光子的貢獻也計算到輕子的質量中，實驗觀測到的結果卻和這一理論符合得相當完美。另一個此類貢獻被實驗驗證的例子是，QED關於在束縛輕子對（例如μ介子素或正子電子偶）中的超精細結構觀測到的蘭姆位移所做的預言。 既然光子對能量-動量張量有貢獻，根據廣義相對論它們也會產生引力場。反過來，光子本身也會受到引力場的作用，在彎曲的時空中它們的路徑也會發生彎曲，在天體物理學中這被應用為引力透鏡。在強引力場中運動時光子的頻率會發生引力紅移，這一點已經在龐德-雷布卡實驗（Pound-Rebka experiment）實驗中得到證實。當然，這些效應並不僅限於光子，而對古典的電磁波同樣成立。