王先智教授| 上海交通大学物理系
只有在热力学极限下,配分函数才会出现奇点,系统产生相变。 ... 的最困难问题之一。1952年杨振宁和李政道提出了著名的相变理论(C.N.Yang and T.D.Lee ... 他们证明,在热力学极限下如果根分布趋近于正实轴,巨正则配分函数出现奇点,系统有相 ...
热力学极限
维基百科,自由的百科全书
热力学极限是指粒子数(或体积)趋向无穷大时的极限。一般宏观物体包含了1023个粒子,可以认为是满足热力学极限的。
杨振宁和李政道证明相变只有在热力学极限下才会发生。
"
展完备的理论"
发掘等式1=0.999...中的物理奥义 精选
精选

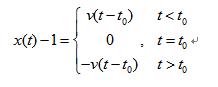
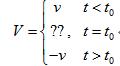
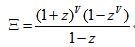
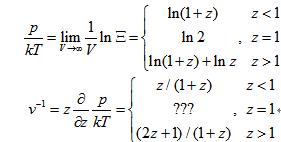
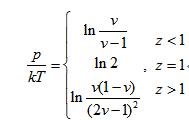
http://blog.sciencenet.cn/blog-3377-537780.html
杨振宁和李政道证明相变只有在热力学极限下才会发生。
"
历史上统计物理学的任务首先在于说明平衡态的性质。早
在人类认识物质的微观结构之前,就形成了描述宏观物体的科
学体系。这就是使用体积、温度、压力、比热、压缩率、膨胀率等
等可以测量的参数,坚持能量守恒、热过程不可逆等基本规律的
热力学体系。热力学主要描述平衡态。对于非平衡态,它除了
指出孤立系统最终必须趋向平衡外,几乎没有给出更为积极的
知识。平衡态的统计物理学,作为热力学的微观基础,已经是发
展完备的理论"
发掘等式1=0.999...中的物理奥义
|||
一只蚂蚁,从坐标原点处往坐标1处爬,它能发现1处的陷阱吗?
高中时期,借得伽莫夫通俗读物《从一到无穷大》一本,很多内容刻尤在骨,封面上的如下一个等式就令人震撼:

近十年来,常有机会面试一些申请或希望进入湖南大学的高三理科生,“如何理解这个等式”之类是我面试题库中的常用题。另一道常用题也出自该书,说有一无限多房间的酒店注满了客人(每房限住一人),可又来了两位客人,还能安排入住吗? 这道题的原始出处据说来自Hilbert.
仅仅学过初等数学,等式1=0.999...不妨这样理解:因为1/3=0.333...,所以1=3x(1/3)=0.999... . 当然,理解不等于证明。初等数学中的一个证明是0.999…=9 x (1/10+1/102+1/103+...)=1.
如果学过高等数学,证明这个等式最高明的方法需要利用到N-ε语言。而涉及这一语言,会遇到两个问题。
问题之一是区间和开和闭。对于半开区间:[0,1) 或者闭区间:[0,1],等式1=0.999...含义不一样。如果一只蚂蚁从0往1爬,对于半开区间,这只蚂蚁不可能到达但是能越来越接近接近1,在x=1这个地方,很可能有一个陷阱;而对于后者,则可以到达。也就是,如果定义一个函数,对于前者,函数是x=1不可能是连续点;对于后者,则有可能。
问题之二有点深奥:在这一点,函数发生了什么事件? 数学上,函数的性质是预先定义好的;在物理上,往往关注一个物理对象,而非抽象的数,例如粒子的运动,一个热力学系统等等。对于这个具体的物理对象能否到达x=1的点,不是一个函数本身就能说清楚,有些问题往往需要通过求导数甚至积分才能看清楚。
所以,弄清函数在x=1处的性质,看似数学,其实能反映出一个物理学家的理论修养。李政道、杨振宁这样的大家由此而创造历史,当然更多的物理教授闹出笑话来而不自知。
一,球与刚性壁间的弹性碰撞
考虑一个质点从x=0处往x=1处匀速地飞,在t=0时与x=1处的刚性壁发生弹性碰撞。位置x对时间t的依赖关系如下:
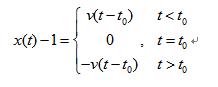
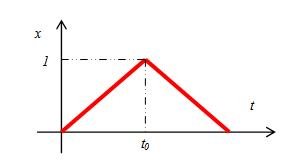
图示如下:

x可以到达1这一点,x本身的定义域为[0,1]. 对x求时间t的导数,得速度:
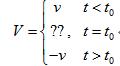
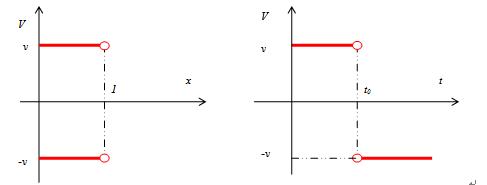
速度空间发生了“灵异”事件:当t=t0时速度无法定义! 也就是从速度空间看,说不清楚粒子有没有到达x=1的点,或者粒子到达后,粒子的速度如何? 图示如下:

进一步揭示x=1处的奇异性,再求导之。结果出现一个“高等”函数——狄拉克d函数d(t-t0):
a= -2vd(t-t0)= -2v2d(x-1)
也就是出现了一个等效力场:
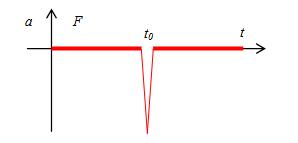
F=ma= -2vd(t-t0)= -2v2d(x-1)
所谓等效力场,一方面它贡献一个冲量,这个冲量刚好改变粒子的运动方向;另一方面它不做功,W=0!
加速度空间图示结果如下:

这是一个极其简单的例子,揭示的道理却是深刻的:蚂蚁能爬到1,爬到后会原路返回! 运动是连续的,但是力场确具有奇异性。力场的奇异性通过对运动的求导数就可以揭示出来。
二,杨振宁-李政道定理
给一个连续函数描述水的流体态,谁是天皇老子能告诉我这个函数何时水处在气相还是液相? 杨-李单位圆定理(西方作者往往称之李-杨定理)是李杨合作的最高成就之一,他们二人的天才在于准确理解了通过求导发现函数奇异性的道理,从而解决了上述问题。
设一个(配分)函数为:
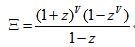
这个函数z=1为可除奇点,也就是它本身完全是一个连续函数。这个函数类似于上例中位置x和时间t的关系。
物态方程是压强p和温度T和(单位质量物质的)体积v间的关系。固定好温度T,考察p和v之间的关系,需要对z求一阶导数。步骤如下:
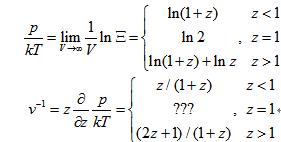
和上面速度v对时间的依赖关系何其相似,“灵异”再次出现:体积v在z=1处不连续!
将z反解出来依赖于v,立即得到一级相变结果:
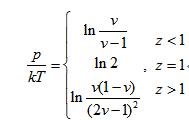
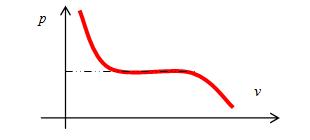
图示结果如下
不但蚂蚁能爬到1,爬到后蚂蚁居然变成了金刚。这个变化也是通过求导数才能看出来。
三,一个贻笑大方的故事
2005年,长沙理工大学物理系有位本科生写信给《物理学报》,指出该刊当年发表的计算三维各向同性谐振子能级的论文有误。《物理学报》对这类稿子通常的处理是:1,原文发表也是请专家评审过的,专家那么容易出错? 2.作者私下沟通一下算了,公开发表“comment”就免了吧。一篇彻头彻尾的错误论文就留在那里至今无人公开指出来。刊物的这种做法其实很不严肃,至少会导致内行对这份刊物权威性的怀疑。
我常有幸看到了论文作者(一位正教授)和那位本科生之间等的若干通讯。作为一名量子力学研究者,我非常佩服那位教授的胆量:对于三维各向同性谐振子能级这种过分熟悉体系的本质上的新发现,发表之前是否要扪心自问一番?
教授的新发现基于建议在r=0点的波函数Y应当满足rY有限,而不是Y本身有限,进而发现一个基态比大家熟悉的基态还要低。除了r=0点,体系的薛定谔方程中的势能的确是各向同性谐振子势能,但是,对波函数求两阶导数,立即发现r=0点出现了一个d函数势能。而三维各向同性谐振子中心带有d函数势能的情况,曾谨言先生已经给出正确处理的途径,那位教授的方法也不对。
在这个例子中,眼睁睁看到蚂蚁靠近1,然后跌到1处的沟里去了。呵呵。
http://blog.sciencenet.cn/blog-3377-537780.html
No comments:
Post a Comment