http://www.dimensions-math.org/Dim_E.htm
[PDF]Option Pricing Models with Jumps in the Context of the ...
math.sun.ac.za/.../Dissertation_Robin_Davies_Jun...
Stellenbosch University
Loading...
by R Davies - 2006
5.1 Using the Convex Hull Function to Find the Optimal Hedge Ratio and the ... that the jumps in the individual security being considered was not correlated to jumps .... The Fundamental Theorem of Asset Pricing states that, for a financial market ... The volatility can be observed from a given path which is what makes the ...Algorithmic Hessians and the fast computation of cross ...
www.tandfonline.com › List of Issues › Table Of Contents
by M Joshi - 2011 - Cited by 11 - Related articles
Sep 30, 2011 - It accurately describes a function's local behavior and is therefore key ... Such derivatives are typically delta hedged, canceling out all .... We will make the notion of state variables precise; however, they ...... The Concepts and Practice of Mathematical Finance, Cambridge, UK: Cambridge University Press.The Concepts and Practice of Mathematical Finance
books.google.com/books?isbn=0521823552
Mark Suresh Joshi - 2003 - Mathematics
However, multiple risk-neutral measures suggest multiple prices so we deduce that there must be a connection between the ... Such a security is known as an Arrow-Debreu security and is essentially a delta function on a given state. What is
按票数排序按时间排序
6 个回答
哈,这个其实是个宏观经济学的概念,所以我修改了话题分类。 @林钊文回答的蛮简略,我详细说一下。
所谓的阿罗德布鲁证券,其实就是针对未来每一种可能存在的情况有一种证券。比如考虑一个简单的两期模型,我们处在第零期,第一期可能有3种情况{H,M,L},这三种情况分别代表三种可能的经济状态。对应这三种状态,分别有三种证券{sh,sm,sl}。在第零期,用{ph,pm,pl}块钱来购买这种证券,第一期,{H,M,L}实现的时候,分别得到回报1块钱。比如第一期H实现了,我就可以得到1/ph的回报率。
以上可以扩充到无限期的情形。
注意在这个建模里面,实际上是把未来的可能离散化了。扩展到连续的情形非常自然,这里用离散的情形加以说明。
与A-D security对应的还有Arrow security,是sequential trade,两者在完备的金融市场下是等价的,不展开叙述。
为什么引入阿罗德布鲁证券?引入了阿罗德布鲁证券之后,我们就引入了完备的金融市场。与之相对应的,不完备的金融市场,比如市场上只存在债券的例子。
有了阿罗德布鲁证券之后,我们就可以用阿罗德布鲁证券来模拟任何的其他证券。比如债券就是{H,M,L}的一个组合,债券实际上就是第一期无论是HML的任何一种,都支付1块钱。所以一单位债券代表一单位H+一单位M+一单位L:{sh,sm,sl}={1,1,1}。这样债券的价格不就是ph+pm+pl么?因为均衡的时候买债券和买那个阿罗德布鲁证券的组合{sh,sm,sl}={1,1,1}是等价的。
奥,差点忘了{ph,pm,pl}是怎么确定的。思路是先解出个体的最优化问题,就是欧拉方程,完了之后代入市场均衡,出清,三个价格就解出来了。
如果想深入下去,可以参考Sargent的Recursive Macroeconomic Theory吧。
另外补充说明,个人觉着如果你是做金融的,这个内容知道一点就好,因为很容易的就可以从阿罗德布鲁证券的一般均衡模型推导出诸如CAPM之类的定价模型。现实应用的话都是用宏观里面这套理论的结论的,没有人再去推一遍这个一般均衡模型。当然你要是做定价的理论除外
Delta位勢阱[编辑]
在量子力學裏,Delta位勢阱是一個阱內位勢為負狄拉克Delta函數,阱外位勢為0的位勢阱。Delta位勢阱問題專門研討,在這種位勢的作用中,一個粒子的量子行為。這是一個常見的理論問題。假若,粒子的能量是正值的,我們想要知道的是,在被Delta位勢壘散射的狀況下,粒子的反射係數與透射係數。假若,粒子的能量是負值的,這粒子會被束縛於Delta位勢阱的阱內。這時,我們想要知道的是粒子的能量與束縛的量子態。
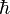 是約化普朗克常數,
是約化普朗克常數,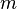 是粒子質量,
是粒子質量, 是粒子位置,
是粒子位置,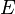 是能量,
是能量, 是波函數,
是波函數, 是位勢,表達為
是位勢,表達為
 是狄拉克Delta函數,
是狄拉克Delta函數, 是狄拉克Delta函數的強度。
是狄拉克Delta函數的強度。
 與
與  。在任何一個區域內,位勢為常數,薛丁格方程的解答可以寫為往右與往左傳播的波函數的的疊加(參閱自由粒子):
。在任何一個區域內,位勢為常數,薛丁格方程的解答可以寫為往右與往左傳播的波函數的的疊加(參閱自由粒子):
 、
、 、
、 、
、 都是必須由邊界條件決定的常數,下標
都是必須由邊界條件決定的常數,下標  與
與 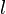 分別標記波函數往右或往左的方向。
分別標記波函數往右或往左的方向。 是波數。
是波數。
當 時,
時,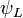 與
與  都是行進波。可是,當
都是行進波。可是,當  時,
時,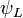 與
與  都隨著座標
都隨著座標  呈指數遞減或指數遞增。
呈指數遞減或指數遞增。
在 处 ,邊界條件是:
处 ,邊界條件是:
 並不是連續的,在位勢阱兩邊的差額有
並不是連續的,在位勢阱兩邊的差額有 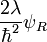 這麼多。這方程式的推導必須用到薛丁格方程。將薛丁格方程積分於
這麼多。這方程式的推導必須用到薛丁格方程。將薛丁格方程積分於  的一個非常小的鄰域:
的一個非常小的鄰域:
 是一個非常小的數值。
是一個非常小的數值。
方程式 (1) 右邊的能量項目是
 时,该項趋向于0。
时,该項趋向于0。
方程式 (1) 左邊是
 的極限,
的極限,
 ,
,
 或
或  。在這裏,粒子的量子行為主要是由 Delta 位勢阱造成的散射行為。稱這粒子的量子態為散射態。設定粒子從左邊入射。在 Delta 位勢阱,粒子可能會被反射回去,或者會被透射過去。我們想要知道散射的反射係數與透射係數。設定
。在這裏,粒子的量子行為主要是由 Delta 位勢阱造成的散射行為。稱這粒子的量子態為散射態。設定粒子從左邊入射。在 Delta 位勢阱,粒子可能會被反射回去,或者會被透射過去。我們想要知道散射的反射係數與透射係數。設定  ,
, ,
, ,
, 。求算反射的機率幅
。求算反射的機率幅  與透射的機率幅
與透射的機率幅 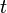 :
:
透射係數是
 ,波數變為複數。設定
,波數變為複數。設定  。前述的振盪的波函數
。前述的振盪的波函數 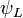 與
與  ,現在卻隨著座標
,現在卻隨著座標  呈指數遞減或指數遞增。為了要符合物理的真實性,我們要求波函數不發散於
呈指數遞減或指數遞增。為了要符合物理的真實性,我們要求波函數不發散於  。那麼,
。那麼,  與
與  必須被設定為 0 。波函數變為
必須被設定為 0 。波函數變為
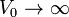 與阱寬
與阱寬  的極限,同時保持
的極限,同時保持  ,就可以從有限深位勢阱的波函數,得到 Delta 位勢阱的波函數。
,就可以從有限深位勢阱的波函數,得到 Delta 位勢阱的波函數。
Delta 函數模型 其實是 氫原子的一維版本 根據 維度比例 由 达德利·赫施巴赫(“Dudley R. Herschbach”)[1] 團隊所研發 此 delta 函數 模型以 雙井 迪拉克 Delta 函數模型 最有用 因其代表一維版的 水分子離子 如以下章節 所述.
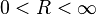 是「核間」距離於迪拉克Delta函數(負)峰值位於
是「核間」距離於迪拉克Delta函數(負)峰值位於  (圖表中棕色所示)。記得此模型與其三維分子版本的關係,我們用原子单位制且設
(圖表中棕色所示)。記得此模型與其三維分子版本的關係,我們用原子单位制且設  。此處
。此處  為一可調參數。從單井的例子,可推論擬設於此解為:
為一可調參數。從單井的例子,可推論擬設於此解為:
 是由偽二次式方程:
是由偽二次式方程:
 。若等價情況(對稱單核),
。若等價情況(對稱單核), 則偽二次式化為:
則偽二次式化為:
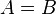 稱為偶態。接著,「-」情況為反對稱於中點的波函數其
稱為偶態。接著,「-」情況為反對稱於中點的波函數其 稱為非偶態(圖中綠色)。它們代表著三維
稱為非偶態(圖中綠色)。它們代表著三維 的兩種最低能態之近似且有助於其分析。對稱電價的特徵能分析解為[2]:
的兩種最低能態之近似且有助於其分析。對稱電價的特徵能分析解為[2]:
 。當非等電價,此為三維分子問題,其解為一般化Lambert W函數(見一般化朗伯W函数章節與相關參考)。
。當非等電價,此為三維分子問題,其解為一般化Lambert W函數(見一般化朗伯W函数章節與相關參考)。
所谓的阿罗德布鲁证券,其实就是针对未来每一种可能存在的情况有一种证券。比如考虑一个简单的两期模型,我们处在第零期,第一期可能有3种情况{H,M,L},这三种情况分别代表三种可能的经济状态。对应这三种状态,分别有三种证券{sh,sm,sl}。在第零期,用{ph,pm,pl}块钱来购买这种证券,第一期,{H,M,L}实现的时候,分别得到回报1块钱。比如第一期H实现了,我就可以得到1/ph的回报率。
以上可以扩充到无限期的情形。
注意在这个建模里面,实际上是把未来的可能离散化了。扩展到连续的情形非常自然,这里用离散的情形加以说明。
与A-D security对应的还有Arrow security,是sequential trade,两者在完备的金融市场下是等价的,不展开叙述。
为什么引入阿罗德布鲁证券?引入了阿罗德布鲁证券之后,我们就引入了完备的金融市场。与之相对应的,不完备的金融市场,比如市场上只存在债券的例子。
有了阿罗德布鲁证券之后,我们就可以用阿罗德布鲁证券来模拟任何的其他证券。比如债券就是{H,M,L}的一个组合,债券实际上就是第一期无论是HML的任何一种,都支付1块钱。所以一单位债券代表一单位H+一单位M+一单位L:{sh,sm,sl}={1,1,1}。这样债券的价格不就是ph+pm+pl么?因为均衡的时候买债券和买那个阿罗德布鲁证券的组合{sh,sm,sl}={1,1,1}是等价的。
奥,差点忘了{ph,pm,pl}是怎么确定的。思路是先解出个体的最优化问题,就是欧拉方程,完了之后代入市场均衡,出清,三个价格就解出来了。
如果想深入下去,可以参考Sargent的Recursive Macroeconomic Theory吧。
另外补充说明,个人觉着如果你是做金融的,这个内容知道一点就好,因为很容易的就可以从阿罗德布鲁证券的一般均衡模型推导出诸如CAPM之类的定价模型。现实应用的话都是用宏观里面这套理论的结论的,没有人再去推一遍这个一般均衡模型。当然你要是做定价的理论除外
Delta位勢阱[编辑]
维基百科,自由的百科全书
定義[编辑]
一個粒子獨立於時間的薛丁格方程為 ;
;
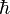 是約化普朗克常數,
是約化普朗克常數,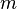 是粒子質量,
是粒子質量, 是粒子位置,
是粒子位置,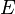 是能量,
是能量, 是波函數,
是波函數, 是位勢,表達為
是位勢,表達為 ;
;
 是狄拉克Delta函數,
是狄拉克Delta函數, 是狄拉克Delta函數的強度。
是狄拉克Delta函數的強度。導引[编辑]
這位勢阱將一維空間分為兩個區域: 與
與  。在任何一個區域內,位勢為常數,薛丁格方程的解答可以寫為往右與往左傳播的波函數的的疊加(參閱自由粒子):
。在任何一個區域內,位勢為常數,薛丁格方程的解答可以寫為往右與往左傳播的波函數的的疊加(參閱自由粒子): ,
, ;
;
 、
、 、
、 、
、 都是必須由邊界條件決定的常數,下標
都是必須由邊界條件決定的常數,下標  與
與 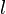 分別標記波函數往右或往左的方向。
分別標記波函數往右或往左的方向。 是波數。
是波數。當
 時,
時,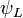 與
與  都是行進波。可是,當
都是行進波。可是,當  時,
時,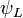 與
與  都隨著座標
都隨著座標  呈指數遞減或指數遞增。
呈指數遞減或指數遞增。在
 处 ,邊界條件是:
处 ,邊界條件是: ,
,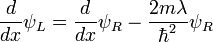 。
。
 並不是連續的,在位勢阱兩邊的差額有
並不是連續的,在位勢阱兩邊的差額有 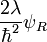 這麼多。這方程式的推導必須用到薛丁格方程。將薛丁格方程積分於
這麼多。這方程式的推導必須用到薛丁格方程。將薛丁格方程積分於  的一個非常小的鄰域:
的一個非常小的鄰域:-
 ;(1)
;(1)
 是一個非常小的數值。
是一個非常小的數值。方程式 (1) 右邊的能量項目是
 。(2)
。(2)
 时,该項趋向于0。
时,该項趋向于0。方程式 (1) 左邊是
 (3)
(3)
 。(4)
。(4)
 的極限,
的極限, ,(5)
,(5) 。(6)
。(6)
 ,
, 。
。
 ,
,
 。
。
散射態[编辑]
假若,能量是正值的,粒子可以自由的移動於 位勢阱外的兩個半空間, 或
或  。在這裏,粒子的量子行為主要是由 Delta 位勢阱造成的散射行為。稱這粒子的量子態為散射態。設定粒子從左邊入射。在 Delta 位勢阱,粒子可能會被反射回去,或者會被透射過去。我們想要知道散射的反射係數與透射係數。設定
。在這裏,粒子的量子行為主要是由 Delta 位勢阱造成的散射行為。稱這粒子的量子態為散射態。設定粒子從左邊入射。在 Delta 位勢阱,粒子可能會被反射回去,或者會被透射過去。我們想要知道散射的反射係數與透射係數。設定  ,
, ,
, ,
, 。求算反射的機率幅
。求算反射的機率幅  與透射的機率幅
與透射的機率幅 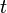 :
: ,
, 。
。
 。
。
透射係數是
 。
。
- 由於模型的對稱性,假若,粒子從右邊入射,我們也會得到同樣的答案。
- 很奇異地,給予同樣的能量、質量、與狄拉克 Delta 函數的強度,Delta 位勢壘與 Delta 位勢阱有同樣的反射係數與透射係數。
束縛態[编辑]
每一個一維的吸引位勢,都至少會存在著一個束縛態(bound state)。由於 ,波數變為複數。設定
,波數變為複數。設定  。前述的振盪的波函數
。前述的振盪的波函數 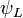 與
與  ,現在卻隨著座標
,現在卻隨著座標  呈指數遞減或指數遞增。為了要符合物理的真實性,我們要求波函數不發散於
呈指數遞減或指數遞增。為了要符合物理的真實性,我們要求波函數不發散於  。那麼,
。那麼,  與
與  必須被設定為 0 。波函數變為
必須被設定為 0 。波函數變為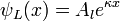 ,
, 。
。
 ,
, 。
。
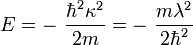 。
。
 。
。
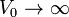 與阱寬
與阱寬  的極限,同時保持
的極限,同時保持  ,就可以從有限深位勢阱的波函數,得到 Delta 位勢阱的波函數。
,就可以從有限深位勢阱的波函數,得到 Delta 位勢阱的波函數。Delta 函數模型 其實是 氫原子的一維版本 根據 維度比例 由 达德利·赫施巴赫(“Dudley R. Herschbach”)[1] 團隊所研發 此 delta 函數 模型以 雙井 迪拉克 Delta 函數模型 最有用 因其代表一維版的 水分子離子 如以下章節 所述.
雙井迪拉克Delta函數模型[编辑]
雙井迪拉克Delta函數模型是用以下薛丁格方程描述: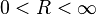 是「核間」距離於迪拉克Delta函數(負)峰值位於
是「核間」距離於迪拉克Delta函數(負)峰值位於  (圖表中棕色所示)。記得此模型與其三維分子版本的關係,我們用原子单位制且設
(圖表中棕色所示)。記得此模型與其三維分子版本的關係,我們用原子单位制且設  。此處
。此處  為一可調參數。從單井的例子,可推論擬設於此解為:
為一可調參數。從單井的例子,可推論擬設於此解為: 是由偽二次式方程:
是由偽二次式方程: 。若等價情況(對稱單核),
。若等價情況(對稱單核), 則偽二次式化為:
則偽二次式化為: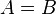 稱為偶態。接著,「-」情況為反對稱於中點的波函數其
稱為偶態。接著,「-」情況為反對稱於中點的波函數其 稱為非偶態(圖中綠色)。它們代表著三維
稱為非偶態(圖中綠色)。它們代表著三維 的兩種最低能態之近似且有助於其分析。對稱電價的特徵能分析解為[2]:
的兩種最低能態之近似且有助於其分析。對稱電價的特徵能分析解為[2]: 。當非等電價,此為三維分子問題,其解為一般化Lambert W函數(見一般化朗伯W函数章節與相關參考)。
。當非等電價,此為三維分子問題,其解為一般化Lambert W函數(見一般化朗伯W函数章節與相關參考)。

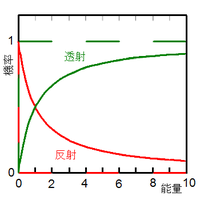
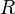 (用紅線表示)與透射係數
(用紅線表示)與透射係數 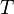 (用綠線表示)隨著能量
(用綠線表示)隨著能量  。經典力學的答案用虛線表示,量子力學的答案用實線表示。
。經典力學的答案用虛線表示,量子力學的答案用實線表示。

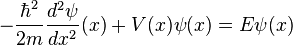
![V(x)=-q \left[ \delta (x - \frac{R}{2}) + \lambda \delta (x+ \frac{R}{2}) \right]](http://upload.wikimedia.org/math/d/e/e/deebbcb61be107530f5ea36cf42992e0.png)


![d_{\pm} (\lambda )~=~{\textstyle\frac{1}{2}}q (\lambda+1)
\pm {\textstyle\frac{1}{2}}
\left\{ q^2 (1+\lambda )^{2}-4\,\lambda q^2 \lbrack 1-e^{-2d_{\pm }(\lambda
)R}]\right\} ^{1/2}](http://upload.wikimedia.org/math/1/c/d/1cdf0b20307ffcb970f913a996bb7a74.png)
![d_{\pm} = q [1 \pm e^{-d_{\pm} R}]](http://upload.wikimedia.org/math/1/b/2/1b25bdd9e628549118cff1f2587d7445.png)

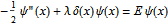
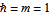
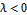
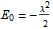
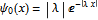
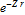
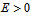
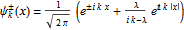
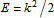
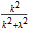
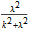
No comments:
Post a Comment