After the free particle, the most elementary example of a one-dimensional time-independent Schrödinger equation is conceptually that of a particle in a delta function potential:
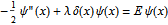
(in units with

). For an attractive potential, with
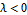
, there is exactly one bound state, with
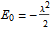
and
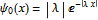
. Note that
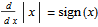
and
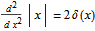
. Since the delta function has dimensions of
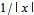
, this solution is considered the one-dimensional analog of a hydrogen-like atom. The bound state, in fact, resembles a cross section of a 1
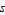
orbital
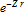
.
For
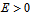
, free particles are scattered by a delta function potential. The positive-energy solutions can be written
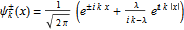
, with

. The amplitudes of the transmitted and reflected waves are accordingly given by
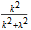
and
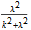
, respectively. Note that these are the same for attractive and repulsive delta funtion potentials, independent of the sign of
[more]
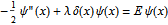 (in units with
(in units with  ). For an attractive potential, with
). For an attractive potential, with 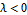 , there is exactly one bound state, with
, there is exactly one bound state, with 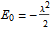 and
and 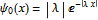 . Note that
. Note that 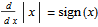 and
and 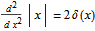 . Since the delta function has dimensions of
. Since the delta function has dimensions of 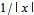 , this solution is considered the one-dimensional analog of a hydrogen-like atom. The bound state, in fact, resembles a cross section of a 1
, this solution is considered the one-dimensional analog of a hydrogen-like atom. The bound state, in fact, resembles a cross section of a 1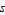 orbital
orbital 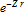 .
.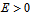 , free particles are scattered by a delta function potential. The positive-energy solutions can be written
, free particles are scattered by a delta function potential. The positive-energy solutions can be written 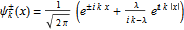 , with
, with  . The amplitudes of the transmitted and reflected waves are accordingly given by
. The amplitudes of the transmitted and reflected waves are accordingly given by 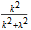 and
and 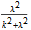 , respectively. Note that these are the same for attractive and repulsive delta funtion potentials, independent of the sign of [more]
, respectively. Note that these are the same for attractive and repulsive delta funtion potentials, independent of the sign of [more]
No comments:
Post a Comment