Sunday, December 14, 2014

热力学 广义坐标Yi, 与yi共轭的广义力 dW =sum 0f Yidyi

 
 
Carnot heat engine 2.svg
经典的卡诺热机
热力学第一定律是能量守恒定律对非孤立系统的扩展。此时能量可以以功W或热量Q的形式传入或传出系统。即：
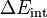\qquad \mathrm \Delta E_{\rm int}= Q + W
式中\Delta E_{\rm int}为系统内能的变化量，若外界对该系统做功，则W为正值，反之为负值。
写成微分形式为：
\qquad \mathrm dE_{\rm int} = \delta Q + \delta W
 
系统的等温过程和量子力学系统的等容过程，我们需要先找到热交换¹dQ和做

功¹dW的量子力学对应的表述。从方程(2.3)我们可以得到

dU =


X
n


(En dPn + Pn dEn) : (2.4)


在经典热力学中，热力学第一定律被表述为
dU = ¹dQ + ¹dW; (2.5)

其中¹dQ = TdS，¹dW =


P
i Yidyi [35]；T 和S 分别是温度和熵；yi 是广义坐

标Yi是与yi共轭的广义力。考虑到（冯诺依曼）熵S和各个本征能级En上的布居

数Pi的关系S = ¡kB


P
i Pi ln Pi，我们可以如下定义量子力学系统的热传递和做

功[36, 37, 38]

¹dQ =


X
n


En dPn; (2.6)

¹dW =


X
n

Pn dEn:


热力学基本过程的量子力学推广
 
2.2.1 量子等温过程


下面我们来讨论一些量子力学系统的基本热力学过程。首先我们要研究的

是量子力学系统的等温过程，也就是量子等温过程。在量子等温过程中，作为

热机的工作物质的量子力学系统，如一个被束缚在势阱中的粒子，始终与一个

温度恒定的热库接触。这个粒子从热库吸热，同时对外做功。在量子等温过程

中，工作物质的本征能级和它在各个能级上的布居数时刻都要发生变化，这样

才能确保系统时刻与热库处于热平衡。现在我们以一个二能级系统为例。我们
分别用jei，jgi和¢来表示这个二能级系统的激发态，基态和两能级间的能级差。

在准静态量子等温过程中，系统在两个能级上的布居数Pe和Pg 服从波尔兹曼分

布关系Pe=Pg = exp[¡¯¢(t)]和归一化条件Pe + Pg = 1。
Posted by at

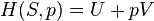
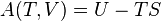
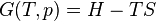
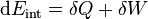
No comments:

Post a Comment

Subscribe to: Post Comments (Atom)