|||
要理解李群流形,先理解“群”。
“群”一直总是一个我没有花精力建立牢固理解的观念。这次顺便解决这个问题。
要定义一个“群”,
首先要定义一个集合,一个符号标志的集合(如整数集合)。这个集合的元素就是每个符号,可以认为是某一个基本状态或某类基本行为的标志。
然后,在这个集合的基础上再定义一种“处理”(如加法+),这种处理,使用集合中任意两个元素,得到另一个元素。
如果这样定义的集合和处理可以满足如下四条规则,则称这个集合和处理是一个“群”。
1.满足封闭性:也就是这个处理所得到的元素,仍然被封闭在所定义的集合中——仍是属于所定义的集合的元素。[a+b=c (a,b,c∈整数集)用系统科学的语言来说,就是不产生“涌现”“突现”]。
2.满足结合律:也就是在用连续两次的处理来按顺序处理三个元素的时候,把前次对前2个元素的处理的结果与第三个元素再进行处理得到最后的结果,会和将第一个元素与“提前处理的后两个元素处理的结果”进行再次处理的结果相同。(a+b)+c = a+(b+c)
3.集合中存在有一个“0元素”。0元素使得对它和任意其他一个元素进行处理的时候,都会得到其他的那个元素,也就是,用它来处理,不会给其他的元素带来任何的变换。(如: 0 + x = x)
4.集合中任何的元素都有反元素。反元素使得将正元素和反元素进行处理的时候,无论先后次序如何,得到的结果都会是0元素。[如a+(-a)=0,(-a)+a=0].
群,可以应用理解为是对自然界中的“变化”用“集合”和“处理”来表达的模型,有2种基本的应用理解:
1.变化发生在“各种不同的状态”之间,变化靠“处理”来驱动。“各种不同的状态”的集合便是一个“状态空间”,处理是联系状态空间中不同状态的跃迁。只是,群,只规定了最基本的2元单类型处理跃迁(其他多元多类型处理的状态跃迁,总可以简化为两元单类型处理的复合结构)。从这个意义上来说,群,实际上就是一个“2元单处理的状态机”。
2.驱动变化的“各种处理”通过复合可以相互转化。这时是将“各种不同的处理”当集合,把将任意两个处理进行复合作为群的处理操作,得到的“驱动变化的处理”仍然是“各种不同的处理”中的一种。这表达了自然界的变化看上去总是循环往复的在驱动操作上的原因的一种假设。
接下来理解“李群”
以前导致我不能专心理解李群的原因之一,可能是我有一个大学的同学的姓名叫“李群”。我看到这两个字的大脑第一反应总是一个人的姓名,而不是一个数学上的“群”概念的一个特例。
摘一段百科上的说明如下:
李群主条目:李群 (数学)李群(为纪念索菲斯·李而命名)是具有流形结构的群,就是说它们是局部上看起来像某个适当维度的欧几里得空间的空间。[69] 这里,作为额外结构的流形结构也必须是兼容的,就是说对应于乘法和求逆的映射必须是光滑的。标准例子是上面介绍的一般线性群: 它是所有 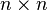 矩阵的空间的开子集,因为它由不等式:det (A) ≠ 0,
矩阵的空间的开子集,因为它由不等式:det (A) ≠ 0,
给出。这里的 A 指示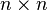 矩阵。[70]
矩阵。[70]
李群在物理中是基础性的: 诺特定理把连续对称与守恒定律关联起来。[71] 在空间和时间中旋转和平移不变性是力学定律的基本对称。它们可以被用来构造简单的模型——比如在一种状况下实施轴对称常常会导致在解用来提供物理描述的方程上的重大简化。v[›] 另一个例子是洛伦兹变换,它有关于两个相互运动的观察者的时间和速度的测量。它们可以用纯群论方式推演,通过把变换表达为闵可夫斯基时空的旋转对称。在忽略万有引力的情况下,后者充当了狭义相对论的时空模型。[72] 闵可夫斯基时空的完全对称群,就是说包括了平移,叫做庞加莱群。通过上述联系,它在狭义相对论中扮演了关键角色,并隐含地用于量子场论。[73] 随位置变化的对称与规范场论一起构成现代物理对相互作用的描述的中心。[74]
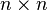 矩阵的空间的开子集,因为它由不等式:det (A) ≠ 0,
矩阵的空间的开子集,因为它由不等式:det (A) ≠ 0,给出。这里的 A 指示
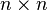 矩阵。[70]
矩阵。[70]李群在物理中是基础性的: 诺特定理把连续对称与守恒定律关联起来。[71] 在空间和时间中旋转和平移不变性是力学定律的基本对称。它们可以被用来构造简单的模型——比如在一种状况下实施轴对称常常会导致在解用来提供物理描述的方程上的重大简化。v[›] 另一个例子是洛伦兹变换,它有关于两个相互运动的观察者的时间和速度的测量。它们可以用纯群论方式推演,通过把变换表达为闵可夫斯基时空的旋转对称。在忽略万有引力的情况下,后者充当了狭义相对论的时空模型。[72] 闵可夫斯基时空的完全对称群,就是说包括了平移,叫做庞加莱群。通过上述联系,它在狭义相对论中扮演了关键角色,并隐含地用于量子场论。[73] 随位置变化的对称与规范场论一起构成现代物理对相互作用的描述的中心。[74]
待续...
No comments:
Post a Comment