| | 當你讀過了上期對於董禮內教授以及他所創造的劇變論的介紹之後,可能你還記得他的劇變論帶來了一大堆新的定性的語言詞彙,我們現在想把一些最簡單、最實用的詞彙介紹出來。當你學會了這些,你就開始會運用劇變論了。
大家對多項式都很熟悉,因此我們就來考慮一個以 x 為變數的多項式 V(x)。假設 V(x) 沒有常數項,因此 V(0)=0。取 V(x) 的導數 V'(x) 以及第二次導數V''(x),我們特別有興趣考慮那些滿足V'(x)=0以及V''(x)=0的點。 舉例來說,令 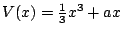 ,則 V'(x)=x2+a,V''(x)=2x。首先考慮 V'(x)=0,則 ,則 V'(x)=x2+a,V''(x)=2x。首先考慮 V'(x)=0,則 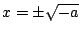 ,因此當a>0時,實根不存在。V(x)的圖形如圖一所示,沒有什麼極大或極小出現。但若a<0,則x有兩個實根,其中 ,因此當a>0時,實根不存在。V(x)的圖形如圖一所示,沒有什麼極大或極小出現。但若a<0,則x有兩個實根,其中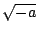 為極小, 為極小,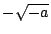 為極大。當 a=0,則有重根,極大與極小相重疊而消失。如果把 V(x) 想成一個位函數(potential function),而其極小代表一種穩定的物理狀態(通常極大不具有任何物理意義),則當 a<0 時,只有一個極小,因此表示我們有一種物理現象或穩定的物理狀態。但是當 a 由負值變為正值,則不再有任何極小存在,這表示此物理現象之消失。反之,若 a 由正變到負,則表示某種物理現象之出現。發生這種出現或消失的不連續變化的所在可藉解 V'(x)=0 及 V''(x)=0 而得;即 x=0 故 a=0。我們稱a=0這點是一個奇異點。在這點附近,a值微小的變化能決定某物理現象之出現或消失。圖二中我們畫出 V'(x)=x2+a=0 的拋物曲線,但通常把這曲線往上平移到 Q 點(平移的原因請讀下一個例子)。上支實線代表極小,下支點線代表極大。這拋物現在 a 軸的投影構成負 a 軸。這樣的圖形叫做摺點劇變(fold catastrophe)模型,O 點(或即 Q 點)稱為摺點。當控制因子(control factor)a 小於 0 時有一個極小存在,但 a 大於 0 時極小消失,因此摺點劇變的模型中的摺點,能用來表達某種現象之出現或消失的不連續變化。 為極大。當 a=0,則有重根,極大與極小相重疊而消失。如果把 V(x) 想成一個位函數(potential function),而其極小代表一種穩定的物理狀態(通常極大不具有任何物理意義),則當 a<0 時,只有一個極小,因此表示我們有一種物理現象或穩定的物理狀態。但是當 a 由負值變為正值,則不再有任何極小存在,這表示此物理現象之消失。反之,若 a 由正變到負,則表示某種物理現象之出現。發生這種出現或消失的不連續變化的所在可藉解 V'(x)=0 及 V''(x)=0 而得;即 x=0 故 a=0。我們稱a=0這點是一個奇異點。在這點附近,a值微小的變化能決定某物理現象之出現或消失。圖二中我們畫出 V'(x)=x2+a=0 的拋物曲線,但通常把這曲線往上平移到 Q 點(平移的原因請讀下一個例子)。上支實線代表極小,下支點線代表極大。這拋物現在 a 軸的投影構成負 a 軸。這樣的圖形叫做摺點劇變(fold catastrophe)模型,O 點(或即 Q 點)稱為摺點。當控制因子(control factor)a 小於 0 時有一個極小存在,但 a 大於 0 時極小消失,因此摺點劇變的模型中的摺點,能用來表達某種現象之出現或消失的不連續變化。
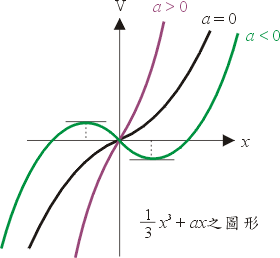
圖一 |
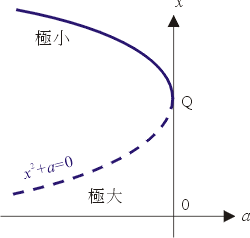
圖二 |
| | |
No comments:
Post a Comment