|
|
|
|
|
|
第七、八章:纤维丛
数学家 Heinz Hopf
描述了他的「纤维丛」(Fibration)。他借着复数的帮忙,在空间内交织出了美丽的圆形排列。 |
|
|
|
|
|
拓扑学
乃研究形变之学门。举例而言,在右边看到的杯子和轮胎是截然不同的两样物体,但是其中一样东西可以透过连续形变,在不弄断任何一处的情况下,变成另外一样;数学家们说杯子与轮胎是同胚(homeomorphic)的。而拓扑学家就是一群分不清楚他们的咖啡杯和甜甜圈的人!!
同样地,这门理论亦经过了很长一段时间才成为一支完全独立、拥有着自己的(通常是性质上的)问题和原创方法的学科。Henri
Poincaré 常被认为是为拓扑学(他称其为analysis
situs)扎下了稳固根基的数学家,虽然在他之前已有许多极具名望的前辈,如 Euler、Riemann、Listing 或 Tait。
我们的主讲人 Heinz
Hopf (1894-1971) 是 Poincaré 在二十世纪上半叶时期最卓越的后辈之一。 |
 |
 |
 |
 |
 |
 |
|
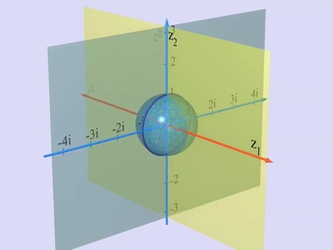
二、C2 內的 S3 球面
我們已經知道,四維空間內的單位 S3 球面即為距原點一單位長度的點之集合。若設此空間內四個實座標為
x1、y1、x2、y2,則這個球面方程就是:
x12 + y12 +
x22 + y22= 1。
但我們可以把 (x1,y1) 想成是一個複數 z1 = x1+iy1,而
(x2,y2) 則為複數 z2 =
x2+iy2。而 S3
球面就可以被想成是一個複數對 (z1,z2) 之集,使得
|z1|2 +
|z2|2 =
1。
|
|
换言之,S3 球面可被视为复二维平面内一单位圆。类推而言(但仅止于类推而言),我们就可以把
S3 球面画成是平面上的一个圆,但请切记:这是一个复平面,而
z1 与 z2 皆为复数。如,轴线
z2=0 就是一条复直线,即一实平面,而它与 S3
球面相交于皆满足 |z1|2 = 1 的点 (z1,0)
,或换言之,皆在 S1 圆上的点。对于轴线 z1=0
与所有型如 z2= a.z1(其中 a
为一复数)的过原点直线而言,上述依然成立。因此,每一个复数 a 都定义了一条复直线
z2= a.z1,其交 S3 球面于一圆。故每个复数
a 皆对应到 S3 球面上的一个圆。此外,虽然轴线方程
z1=0 型非如此,它仍可被视为是对应到了无限的 a
值之情况(垂直的轴线不就是一条有着无限斜率的直线吗?)。
所以 S3 球面上是充满着圆的。对每一个
S2 内的点,即,对所有的复数 a
值(可取无穷大值),都有相对应的一个圆。没有两个这种圆会在有不同的 a
值之情况下相同。这种分解三维球面成圆的动作被称为 Hopf 纤维化 (fibration)。 |
 |
| 請按上圖觀賞影片。 |
|
 |
回想:若设 X 与 Y 为两集合,则一个由
X 到 Y
的一个映射(map) f,又常记为 f : X
→ Y,就是一条可让我们将
X 内之点 x 和
Y 内之点 f(x) 之间建立关系的规则。
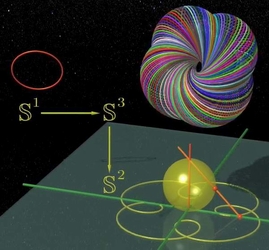
例:考虑 Hopf 映射 f : S3 →
S2。它建立了一点 (z1,z2) 与点
z2/z1 之间的关系。
关于这点有两个解释:
第一,S3 上的一点就是二维复平面上的一点,而可以被其复坐标
(z1,z2) 所描述。
第二,我们藉由球极投影可以看到,若于平面添加一无穷远点(point at
infinity),则我们就可以得到一个 S2 球面。而当然,复数
z2/z1 只有在 z1
之值不为零的情况下方属定义良好(well defined)的,若 z1 值为零,则我们就把
z2/z1 定为无穷远点。所以 z2/z1 实可定义出
S2 上之一点。 |
对于 S2 上每一点 a,于
S3 内使得在 f 下的像(image)为
a 的点集(即 a 之原像[pre-image]),是
S3 内的一个圆。我们称此点集为 a
上的纤维(fiber)。这与上述解释之关联就是:所有在一条线 z2=
a.z1上的点皆使得 z2/z1 为常量(这很明显,因为它根本就等于
a !)。
|
|
|
|
|
影片先请我们仔细观察这个「纤维丛」。每个 a 值皆对应到一在
S3 内之圆。我们要怎么将其加以具象化呢?当然是靠球极投影法了!我们由
S3
投影至接于投影极点对面的极点之三维切空间上。此投影是空间内的一个圆。您可以好好地欣赏它(别忘了那些蜥蜴!)。当然,这个
S3
上的圆有可能正经过北极点,因而造成其球极投影呈一直线(即少了一个点的圆……那个点已经跑到无穷远处了!)。
|
 |
|
 |
几个序列阐明了此纤维丛:
首先,我们只看到一个 Hopf 圆。它与 a 值相对应。这个点
a 在 S2
上移动(请记得:它是一个加上了一无穷远点的复平面),而我们就看到此圆在空间中移动,不时地当在 a
通过无穷远点时变成一直线。
然后,我们看到了两个正同时移动的 Hopf 圆。它们与两个 a
值相对应。您可以在屏幕底部看到两个正在移动的 a
点,而此二圆也同时跟着移动。顺便一提,请注意:这两个圆是像铁链般地互相链结在一起的。我们不能在不扯断它们的情况下将它们分开。
然后,我们看到了三个舞动中的 Hopf 圆。它们与三个 a
值对应……这些圆时而疏离、时而凑近……。 |
| 单机图片观赏影片。 |
|
最后,我们同时看到了一大堆 Hopf 圆。a
值被随机地选定而出,而相对应的圆就陆续跟着出现。我们就可以「看」到空间中充满了圆,而这些圆并不相交。我们也终于可以了解「纤维丛」这个词的来源了:所有的圆都互相交织在一起,就像是织物的纤维一般:由局部上看来,它们整齐的像一束面条。当初以
Hopf 映射为原形发展而成的纤维丛之概念,已成为了拓扑学与数理物理(mathematical
physics)中的一个核心概念。有些纤维丛更为复杂,存在于更高维的空间之中,但对这个历史性的例子能有一个清楚的观念无疑是深具启发意义的!
把实平面想成复数直线固然有用,但将实四维空间想成复二维平面更是有用多了! |
 |
|
|
|
 |
为了更透彻地理解 Hopf 纤维丛 f : S3 →
S2,考虑 S2 内一条纬线
p,以及 p 在
f 下的「原像」,即于 S3 内满足在
f 下之像是属于 p 的点集。由于
S2 内各点的原像(各纤维)皆为一 Hopf 圆,而又由于一条纬线也同时是一个圆,故
p 之原像乃是由一族圆所组成,其因一关于圆 p
的参数而变。因此它是 S3 内的一个曲面。一如往常地,在影片中它被球极投影到了三维空间内。
当一纬线非常地靠近 S2
的一个极点(而因此是一个很小的圆)时,p
的原像将会呈一细小管状,紧临着该极点上的纤维。当该纬线渐渐地变大,直到变成赤道,接着又渐渐变小,向另一个极点靠近时,管子就会跟着渐渐变大,然后再变小,而在最后又变成细管状。这些管子是
S3 内的环面,不过,我们只能观察它们于三维空间中的投影,所以它们在靠近
S3 的北极点处时看起来并不是非常地完美无暇。 |
| 請按上圖觀賞影片。 |
|
严格来说,一个环面是一个空间中的回转曲面,由将一圆绕行与其共面之轴线而得来。环面上面的一点有两个角坐标:一个是用来描述在圆上的位置,而另一个则是用来描述此圆被旋转的角度大小。
这与经纬之概念的相似处是值得注意的。居住在环面上(而非球面,如我们的地球)的生物也会发明出经线、纬线、经度、纬度的概念。 |
|
事实上,拓扑学家们常称一「环面」为一与回转环面「同胚」的曲面,例如:一个咖啡杯!当他们所指的是由回转一个圆而得来的环面时,他们会说回转环面(torus
of revolution),以避免混淆。
我们可以在一个回转环面上清楚地看到两族圆:一族经线(蓝)与一族纬线(红)。在这个情况下,要区分经纬会比较困难一点。在球面上,这很容易:所有的经线皆通过两个极点,但是,回转环面上是没有极点的!于是,我们约定(但这只是一个习惯)将蓝色的圆都称为「经线」,因为它们处于的平面都含有回转环面之对称轴,而红色的圆则为「纬线」,因为它们处于的平面皆与该轴垂直。
一个令人惊奇几何事实是:在回转环面上还有可能找的出许多其它圆…本章解释了如何作出这些圆。 |
 |
|
回想一下描述 Hopf 纤维丛的公式。从复数坐标而言,它将 (z1,z2) 送到可被视为是
S2 内的一点 a。在
S2 内定一条纬线
p,就等同于定一复数之模,故一条纬线的原像可被型如下的公式所描述:
|z2/z1| =
常数。
例如,可取该常数值为1,使
z1 与 z2 有同样的模。但别忘了
|z1|2 + |z2|2 = 1,
故
z1 和 z2
的模皆等于√2/2。因此,此纬线之原像集包含了点 (z1,z2),其中
z1和 z2
皆为在半径为√2/2、以原点为圆心的圆上之动点。故,由此可见,纬线的原像就是一个曲面,其可被两个角度所参数化:因此,就如同影片中所见,它是一个环面。若令
z1 为定值,则可得到 S3 内之一圆,而若是令
z2 为定值,则可得到另一个圆。不过,目前对于四维回转环面而言,我们无法说出哪一个圆是纬线、哪一个是经线。
将该环面由北极(其坐标为(0,1))球极投影至三维空间内之时,我们不难看出:该环面之投影不单只是与一环面同胚而已,它还其实根本就是一个回转环面。绕着哪个轴回转呢?即通过北极点的
Hopf 圆的球极投影:这个投影无疑是一条直线!所以,我们能知道该如何把回转环面想成是一条纬线在 Hopf 映射下的原像了。
一个由这种解释衍生的结果是:对于该选定纬线上之每一点而言,相对应到的 Hopf 圆很明显地是被包含在此回转环面内的。我们刚发现了回转环面内的其它圆……。
于下列出几个公式。考虑空间内一由从北极点(0,1)投影
|z1| =
√2/2;
|z2| =
√2/2
而生成的回转环面。
我们接着考虑将 (z1,z2) 送到
(ω.z1,z2) 的映像,其中 ω
描述了所有模皆为1的复数所形成之圆。因 z1 和 z2
之模并不会变动,故这些映射将保有 S3 球面。型如
(0,z2) 之点亦不会改变。我们正在讨论的就是于四维空间中绕着复直线
z1=0
的旋转变换。因为该直线通过了投影极点(0,1),所以它的球极投影并不会是一个圆,而是一条直线。因此,这些与
ω
参数相关之映射就定义了在我们的空间中绕行着一条直线的旋转变换。而由于这些旋转变换亦保留了我们目前正在考虑的回转环面,所以
z1=0 就是这个环面的对称轴! |
|
如此一来,通过 (z1,z2) 的纬线就是型如 (ω.z1,
z2) 的点之集合,其中,ω 属于所有模为1的复数组成之圆。通过
(z1,z2) 的经线则是型如 (z1, ω.z2)的点之集合。
通过 (z1,z2)的 Hopf 圆是型如 (ω.z1,
ω.z2) 的点之集合(请注意:若将 z1 与
z2 同乘以 ω,则
z2/z1将仍不变,因此所有的这类点在 f
下的像皆相同;它们都属同一纤维)。还没完;过每一点 (z1,z2),我们还可以考虑「对称」的圆,其乃是由型如
(ω.z1, ω-1.z2) 的点所组成。这给出了回转环面上的第四个圆。
我们刚才证明了:对一回转环面上之每一点,我们都可以画出四个通过该点之圆:一条经线、一条纬线、一个 Hopf 圆、以及一个对称于
Hopf 圆的圆。 |
 |
|
 |
这项事实在很久以前就已经被发现了。这些圆通常被称为 Villarceau
圆,以纪念一位十九世纪的数学家。但读者应早就了解到:在数学中,创造与内化的过程是如此地漫长且复杂,因此,一个定理很少是实由其名而来的。所言不假,史特拉斯堡大教堂(Cathedral
of Strasbourg)博物馆之一阶梯(其历史可追溯至十六世纪)便告诉了我们:雕刻家们不需要等到 Villarceau
的发现才开始在环面上雕刻圆形! |
|
本章第二部份采用了不依赖 Hopf 纤维丛的一个方法来描绘出 Villarceau
圆。从一个回转环面开始,我们用一个双切平面把它剖开来,然后观察其截面。该截面含有两个圆。
怎么证明这项事实呢?我们可以列出方程式,然后计算(参见 此处)……但是,呃,这并不是非常地具有启发性。不过,藉由代数几何中的几个概念,如「圆点(cyclic
points)」,我们就可以用一个非常出色的方法,在几乎不用计算的情况下证明出该定理。这些点不只是无穷远点,还是虚点!由此可见,想象力是无边无际的!欲阅读利用了这类构想的
Villarceau 定理之证明,请参见 此篇文章。 |
 |
|
 |
给定一三维空间中之曲面,则我们可将其视为一在 S3 空间内(在添上一无穷远点之后)的曲面。因
S3
乃四维空间内的单位球面,故我们可以先利用四维旋转变换使其旋转,然后再一次地将其球极投影至三维空间中!这样我们就会得到另一个曲面。这个曲面与它原来的样子相类似,但是并不一样!若从一回转环面开始操作,则我们会得到的曲面就是所谓的
Dupin
四次圆纹曲面。这种曲面于十九世纪时期被广泛地研究过。因球极投影把不通过极点的圆变换为圆,故回转环面上之四族圆的存在性就意味着:在四次圆纹曲面上亦存在着四族圆……
因此,三维空间中一环面即可被想成是四维空间内可旋转的
S3 内之一曲面。若藉由球极投影法辅助观察之,则我们就可以看到一段 Dupin
四次圆纹曲面正在变形的画面。一旦当该曲面通过了投影极点时,我们就会发现它会膨胀至无限大,而接着又再次变回原样。不过,这时您会发现:它的经纬线已经被互相对调,而一整个环面则是已经被从里面翻到外面去了! |
| 請按上圖觀賞影片。 |
|
空间内的圆之几何是非常美丽的。有时候它亦名保反(anallagmatic)几何。关于这门学问,我们有一箩筐的事情可以讲!
五、Hopf 与同伦
在影片中,我们不幸地并无提及 Hopf 之动机。我们在此对其做出一些简短的讨论,以做为本文结尾。
在拓扑学中,我们经常考虑两 拓扑空间 X 与
Y 之间的映射。我们不在这里给出定义,不过,您可以把 X
和 Y 分别想成是(举例而言)n 维和
p
维的球面。当然了,至此我们只有讨论过零、一、二与三维的球面,不过,您应该早就料到了故事并不会就到此结束…&
hellip;当然,研究完全没有任何限制条件的映像并不会引起太大的兴趣,所以,我们将只专心讨论连续映像(continuous
maps),即所有满足当 x 的变动量足够小时,点
f(x) 并不会作出剧烈变动的映射。例如:对一实数
x,若 x 非 0,则将其送至 +1,而若
x 为 0,则将其送至 -1 的映像并不是连续的,因为它在我们经过 0 的时后「跳」了一下。但是,将
x 值送至其平方值 x2
的映射就是连续的;若我们稍微地变动一数,则其平方值只会稍加改变。拓扑学中的其中一个基本问题涵括了对于拓扑空间(如球面)之间的连续映射之探讨。
拓扑学其实简单多了:它以了解 同伦(homotopies)
为目标。又是一个代表着很简单的事物的复杂名词!假设今给定两个由 Sn 球面到
Sp 球面的连续映射 f0 与
f1。如果我们可以把 f0 形变为
f1,则我们就称 f1 与
f0 是同伦的。换言之,这代表着:存在一族与一参数
t(其取值范围在0与1之间)相关之映像 ft,将
f0 与 f1 连结起来。更确切地说,这表示
Sn 内的每一点 x 和每一个介于0与1之间
t 值皆可以与一点 ft(x) 相配,定义出一个
x 和 t 的连续映射,使得当 t=0 时,我们便可得到
f0,而当 t=1 时,我们即可得到
f1。 |
|
|
举例而言:一映射 f : S1→
S2
只不过是一个二维球面上的一条封闭曲线而已。例如,f0 可以是一个把
S1 上所有点 x
都送到北极点的一个映射:这就是所谓的常值映射(constant map)。而
f1 则可以是将 S1 圆送至
S2
上之赤道的映射。若此二映射是同伦映射,则这就代表着我们可以把赤道渐渐的形变成北极点,如右图。事实上,这总是有可能的;每一对由
S1 到 S2 的映射都是同伦的。拓扑学家们这么说:所有
S2 上面可画出的曲线皆与常值曲线同伦,或是,S2
是单连通(simply connected)的。应该不难说服自己:对于所有维数大于等于二的
Sp 球面,上述仍成立。(亦请参考 这页) |
|
 |
|
|
S1 与 S1
之间的一个映射就等效于将圆上的一点变换为圆上的另一点:某种程度上,这就是圆上的一条曲线。这种映射有一个度数(degree):即该映像所绕行的完整圈数。例,常值映射完全不会绕行:它的度数是0。将每一点送至自身之处的恒等映射(identity
map)理所当然地是绕行了一周;它的度数是1。把任何模为1的复数都送至其平方的映射将把幅角乘以二。故,若绕行圆一周,则平方映射就会绕行两圈:它的度数是2。当一映像受到形变时,它的度数并不会改变,因此,在所有由
S1 到 S1
的映像中,存在着无法被形变为常值映射的映射……要看得出两个度数相同的映射是可以各自形变成对方的,则稍加困难。 |
|
 |
但是 S2 与 S2 之间的映射又是如何呢?与
S1 到 S1
的情况相似地,我们亦可定义出一个度数,即使问题已不再是要数出「圈数」了:现在问题在于要数出 f
之像「覆盖」球面的次数多寡,而这并不容易定义。最简单的例子是恒等映射:任一点皆被该映射送至原处:它的度数是1。我们可猜想:S2
上的恒等映射,是无法在不把球扯断的情形下,被形变成常值映射的。但是还是要有办法证明才行!
Heinz Hopf
在1931年时证明了这个惊人的事实:某些由 S3 到
S2
的映射是不能被连续形变成常值映射的。当然,他举出的例子就是我们才刚认识的纤维丛。渐渐地,这个对象就在数学还有物理中开始扮演起非常重要的角色。
每对纤维都是互相链结在一起的特质就是使得 Hopf 映射 f :
S3→ S2
无法被形变为一常值映射的关键。要给出一个具有说服力的理由还需要一个颇为冗长的解释!这本书
里给出了一个完整却艰涩的阐述,或可于 Hopf 的 原版论文 中找到一个证明,与其它许多细节。 |
|
对于 Sn 与 Sp 之间的映射,其中
n 与 p
皆取任意值,我们又有何了解呢?已有很多事实被发现,但我们与达全盘了解的距离还很长:「球面间的映射之同伦类(homotopy classes)」仍然是一个大谜题!
「纤维丛」只是 Heinz Hopf 做出的贡献的其中之一而已。他对于二十世纪时期的数学有着深远的影响。
|
|
|
|






No comments:
Post a Comment