法蘭克的數學世界
主要用中文寫的數學部落格
光滑流形(Smooth Manifold)

導言
今天要跟各位談的是一種比較特殊的拓樸空間,這個拓樸空間呢叫做流形(Manifold)。這個拓樸空間特別的地方就在於它每個點的附近看起來都像歐氏空間,換句話說,他是由一些歐氏空間所黏貼而成。舉例來說,我們所生長的地球就是一個具有這樣性質的空間。想一想,我們生活在地球上,我們自己覺得是生活在平地上並沒有感覺到我們所生活的空間是彎曲的。由於這個空間局部上看起來很像是歐氏空間,所以我們可以賦予這空間座標系的概念。例如,我們熟知的地球,有經度跟緯度這樣的概念,而經緯的概念就是座標系的概念。在介紹一般的流形概念之前,讓我們先來看一下,在歐氏空間中如何定義曲線與曲面的概念。歐氏空間的參數化曲線
令假設
範例:令
令
如果 均是定義在
均是定義在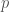 點附近的光滑函數,則我們可以驗證:
點附近的光滑函數,則我們可以驗證:
(1) 

(2) 
於是切向量就被賦予了新的意義。當然這意義是人工的,我們只是把切向量看成是對函數做微分。這樣的目的是為了在抽象的流形中引入切向量的概念,隨後我們會見到。
歐氏空間中的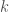 維曲面
維曲面
假設(1)
(2)任意的
則我們稱映射
範例:令
當你把不同的
定義:令
範例:
光滑流形的一般定義
嚴謹的流形定義如下:假設假設

以下我們談到的
定理: (Whitney Embedding Theorem) 假設
這個定理告訴我們,所有的光滑流形都是某個歐氏空間中的光滑曲面。
光滑流形的環空間定義方式
令定理:函數空間
如果
定義:如果
定理:
假設
換句話說,環空間除了具有拓樸空間的概念外,我們也定義了他上面由環層
任給一個
定理:光滑流形與其上的光滑映射構成了一個範疇。
基本上來說,光滑流形可以視為某一類的環空間 滿足:存在一個
滿足:存在一個 開覆蓋
開覆蓋 使得對任意的
使得對任意的 ,環空間
,環空間 與環空間
與環空間 是同構的。換句話說,光滑流形局部上來說,他跟歐氏空間一樣,他上面的函數空間跟歐氏空間上的光滑函數所形成的空間也是一樣的(在同構意義下)。換句話說呢,如果給一個
是同構的。換句話說,光滑流形局部上來說,他跟歐氏空間一樣,他上面的函數空間跟歐氏空間上的光滑函數所形成的空間也是一樣的(在同構意義下)。換句話說呢,如果給一個 上的可微分函數,我們取局部座標系
上的可微分函數,我們取局部座標系 那麼
那麼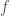 就可以寫成歐氏空間中的可微分函數
就可以寫成歐氏空間中的可微分函數 這樣的對應關係
這樣的對應關係
是一個代數上的同構關係。不僅如此,透過這樣的代數關係,我們把歐氏空間中的微積分學就這樣的搬到了光滑流形上。局部上來說,由於光滑流形看起來就是歐氏空間,流形上的光滑函數就是歐氏空間中的光滑函數。你當然希望你的微積分在座標變換下的意義是不變的,因此,你會要求你的函子 是一個層。基本上來說,層的概念就是透過微分流形才產生的。而層的一些條件就是在告訴你,微分流形上的微積分學是良定(well-defined)的(在座標變換的意義下不變)。從現在開始,你知道的微分流形的概念,把古典微積分學套入,你就可以開始研究微分幾何。
是一個層。基本上來說,層的概念就是透過微分流形才產生的。而層的一些條件就是在告訴你,微分流形上的微積分學是良定(well-defined)的(在座標變換的意義下不變)。從現在開始,你知道的微分流形的概念,把古典微積分學套入,你就可以開始研究微分幾何。
5 responses on “光滑流形(Smooth Manifold)”
發表迴響
%d bloggers like this:


的manifold是不是要Housdorff該定理才會對?(因為這裡的mainfold好像沒有特別說是Housdorff)
另一个微分算子是 Θ 算子,定义为
有时候这也称为齐次算子,
“—-http://zh.wikipedia.org/wiki/%E5%BE%AE%E5%88%86%E7%AE%97%E5%AD%90
——
thanks for your this post with picture, very good, and I have to read it again, but I like it a lot.
I understand 微分算子 as 拉普拉斯算子, what is 齐次算子 as qutoed in the above wiki?
a good article:
[PDF]
物理激发的数学 – 中国科学院数学研究所
http://www.math.ac.cn/index_E/post/…/PPT110907.pdf – 轉為繁體網頁
檔案類型: PDF/Adobe Acrobat – 快速檢視
形的A- 亏格恰好是黎曼流形上狄拉克算子. 的指标。 几何分析中许多有效的方法都是受物理学家. 启发的如. 启发的如平均曲率流是物上首先. 平均曲率流是物上首先 …