不過話說回來,講線性代數的書不一定會講到這個幾何意義,因為定義行列式幾行就寫完了,但是定義面積(體積),尤其是高維空間的面積(體積)是一件相當麻煩的事情。
如果讀者只讀過線性代數,那麽不妨這樣直觀感受一下行列式。而如果讀者讀過實變函數或者測度論,那麽這個結論可以作為一道不錯的習題。
外积典型的称呼张量积或有类似势的运算如楔积。这些运算的势是笛卡尔积的势。这个名字相对于内积,它是有相反次序的积。
一个长方形的纸箱,它的体积应该怎样算?公式?
纸箱的体积,就是两个长方体的体积相减就行了,长方体的体积公式:V=长*宽*高 的体积应该=长*宽*高 长乘宽乘高! 设底为a.宽为b.高为h.体积为V. 所以V=abh. 长为最长的边.宽为长边于底面的临边,高为长边的另一临边. 线乘线等于面积,面积乘面积等于体积,所以纸箱的体积是一个角引出3条边长度的乘积的值。 长乘宽乘高l=?立方 底面积乘高 体积V=长乘以宽乘以高 体积=长*宽*高 一般来说长方形纸箱的体积是该长方形的面积乘以他的高度,当高度为0时,其体积等于0.。
外积典型的称呼张量积或有类似势的运算如楔积。这些运算的势是笛卡尔积的势。这个名字相对于内积,它是有相反次序的积。
平凡解是Ax=0中的零解,即x=0。
中文名
平凡解
外文名
Trivial Solution
定 义
Ax=0中的零解,即x=0,称为平凡解
应用学科
数学
数学范畴
矩阵代数
矩阵代数的中的定义,
因为任何线性空间的子空间都过零点, 所以明显的等于0的时候解是成立的,但这显然没什么意义,说这个0解是平凡的,
通俗来讲,如果方程组AX=0, 只有当X=0的时候才成立,就说方程组AX=0只有平凡解(trivial solution),此时肯定有行列式|A| 不为零。相反如果方程组AX=0存在非零解,也就是说存在不为零的X也可以使方程组AX=0成立,则说方程组AX=0存在非平凡解(nontrivial solution),此时肯定有系数矩阵行列式的值|A|=0。
行列式的運算公式與性質| 線代啟示錄
https://ccjou.wordpress.com/2010/12/01/行列式的運算公式與性質/
2010年12月1日 - 本文的閱讀等級:初級在線性代數發展歷史中,行列式和矩陣理論一直有著 ... 本文從一個簡單的面積計算問題推導行列式的運算公式,這麼做雖有違 ...行列式的應用(Applications of Determinant) | 科學Online ...
highscope.ch.ntu.edu.tw/wordpress/?p=56727
2014年9月17日 - 表示平面上三角形的面積 e1 、 e2 ,則 E3 面積 E4 ( E5 乘以 E6 的絕對值)。 【證明】向量积- 维基百科,自由的百科全书
zh.wikipedia.org/wiki/向量积
轉為繁體網頁
与点乘不同,它的运算结果是一个偽向量而不是一个标量。叉乘的 ... 2.1 几何意义; 2.2 代数性质; 2.3 拉格朗日公式; 2.4 矩阵形式. 3 高维 ... 为边的平行四边形的面积。轉為繁體網頁
行列式求面積- Yahoo!奇摩知識+
https://tw.knowledge.yahoo.com/question/question?qid=1512122200031
求證明:知三角形頂點座標,可用二分之一4行2列行列式絕對值代表面積.行列式的運算公式與性質
本文的閱讀等級:初級
在線性代數發展歷史中,行列式和矩陣理論一直有著密切的關係。行列式概念最早出現於解線性方程組的過程中,十七世紀末,日本數學家關孝和與德國數學家萊布尼茨 (Gottfried Wilhelm Leibniz) 的著作就已使用行列式來確定線性方程組解的個數以及形式[1]。十九世紀以後,矩陣的引入使得更多的行列式性質被發現,行列式的發展遂漸趨完善。今天多數線性代數教科書都會開闢一個專門討論行列式的章節,但主要的目的並非求解線性方程組,而是為了順利導入矩陣的特徵多項式。不過,美國數學教授阿斯勒 (Sheldon Axler) 卻抱持反對的態度,他認為行列式是線性代數核心原理的推導結果,而不是行列式推導出線性代數的核心原理。1994年,阿斯勒發表〈斷絕行列式〉 (Done with determinants!),該文嚴厲抨擊行列式目前於線性代數的「地位」,之後並獲得不少數學家的共鳴和迴響。阿斯勒反對行列式的理由在於行列式難以理解,不具直覺,而且常在缺乏明顯動機的情況下被引用。不僅如此,行列式和線性代數理論的基調不甚相合。行列式的計算公式與主要的矩陣運算無關,它像是從一堆矩陣元拼貼出來的蒙太奇,讓人困惑如此怪異的公式究竟是怎麼冒出來的。雖然我們無法改變或簡化行列式公式,但仍可嘗試編排出易於理解的推導過程。本文從一個簡單的面積計算問題推導行列式的運算公式,這麼做雖有違行列式誕生的初衷,但此法能夠豐富行列式的幾何直覺解釋並顯現行列式的一些重要性質。
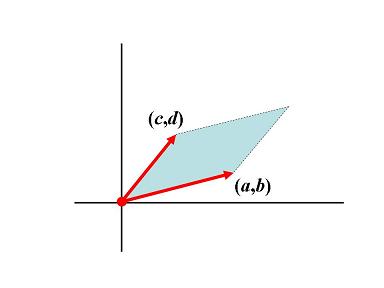
設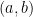 和
和  為平面上的兩個向量 (見下圖)。考慮矩陣
為平面上的兩個向量 (見下圖)。考慮矩陣 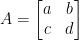 ,我們定義函數
,我們定義函數 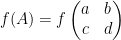 為
為 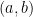 和
和  所張的平行四邊形面積。通常吾人總會揀選最便捷的解題途徑,不過在此我們採用一種比較不尋常的作法:先找出此函數必須滿足的條件,等待條件充足後,再著手推導面積函數
所張的平行四邊形面積。通常吾人總會揀選最便捷的解題途徑,不過在此我們採用一種比較不尋常的作法:先找出此函數必須滿足的條件,等待條件充足後,再著手推導面積函數  的公式。
的公式。
首先考慮最簡單情況: ,
, ,兩相互垂直的標準單位向量張開單位正方形,於是有下面的性質。
,兩相互垂直的標準單位向量張開單位正方形,於是有下面的性質。
性質一: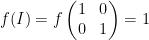
再看另一個極端情況: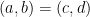 ,兩向量完全重合表示所張的平行四邊形面積等於零。
,兩向量完全重合表示所張的平行四邊形面積等於零。
性質二:若 有相同的兩列 (row)[2],則
有相同的兩列 (row)[2],則  。
。
上述兩個性質仍不足以規範函數 ,我們需要更多有關平行四邊形的幾何性質,特別是所夾向量改變時,平行四邊形面積如何隨之變化。下圖顯示向量
,我們需要更多有關平行四邊形的幾何性質,特別是所夾向量改變時,平行四邊形面積如何隨之變化。下圖顯示向量 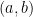 的長度縮放
的長度縮放 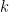 倍,對應的平行四邊形面積亦等比例改變,因此
倍,對應的平行四邊形面積亦等比例改變,因此  滿足下列關係:
滿足下列關係:

從基礎幾何學可知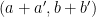 和
和  所張的平行四邊形面積恰為
所張的平行四邊形面積恰為 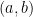 和
和  所張的平行四邊形面積與
所張的平行四邊形面積與 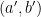 和
和  所張的平行四邊形面積之和 (見下圖),亦即
所張的平行四邊形面積之和 (見下圖),亦即

運用對稱原理,同樣也有
 我們將上述線性關係合併為一個性質。
我們將上述線性關係合併為一個性質。
性質三:考慮 的任一列,當其他列都固定時,
的任一列,當其他列都固定時,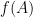 為該列的線性函數。
為該列的線性函數。
這裡要特別強調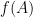 並非矩陣
並非矩陣  的線性函數,也就是說,
的線性函數,也就是說, 和
和  不成立。對於
不成立。對於  階矩陣
階矩陣  ,性質三說明
,性質三說明
 推廣至
推廣至  階矩陣
階矩陣  ,則有
,則有 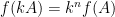 。
。
如果將 的兩列對調,
的兩列對調,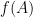 是否改變?交互使用性質二和性質三可以推出下面的結果:
是否改變?交互使用性質二和性質三可以推出下面的結果:
 性質四是性質二和性質三的必然結果。
性質四是性質二和性質三的必然結果。
性質四:交換 的兩列改變
的兩列改變 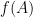 的正負號。
的正負號。
性質四迫使函數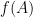 必須是「有號」(signed) 面積。若將右手拇指外的四根手指向手掌彎曲的方向視為由第一列至第二列的旋轉方向,則面積為正,反之,面積為負,此即為「右手定則」。
必須是「有號」(signed) 面積。若將右手拇指外的四根手指向手掌彎曲的方向視為由第一列至第二列的旋轉方向,則面積為正,反之,面積為負,此即為「右手定則」。
準備就緒,現在我們可以利用上述性質推導 函數。類似性質四的推演過程,先運用性質三來分解
函數。類似性質四的推演過程,先運用性質三來分解  ,如下:
,如下:
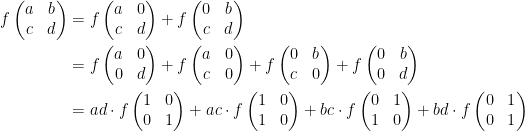 由性質二可知
由性質二可知  ,
, ,再由性質四和性質一,
,再由性質四和性質一,
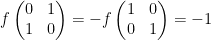 最後導出
最後導出 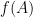 的計算公式:
的計算公式:
 這就是大家熟知的二階行列式公式。為方便辨識,我們改以
這就是大家熟知的二階行列式公式。為方便辨識,我們改以 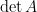 或
或 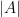 替代
替代 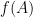 :
:
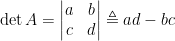 推導行列式公式的過程雖然使用了性質四,但性質四也是由前面三個性質所導出,所以性質一、二和三唯一決定行列式的計算公式。稍後我們將以歸納法推演出更高階行列式的計算公式。
推導行列式公式的過程雖然使用了性質四,但性質四也是由前面三個性質所導出,所以性質一、二和三唯一決定行列式的計算公式。稍後我們將以歸納法推演出更高階行列式的計算公式。
接著我們推導行列式的其他性質。不論前述的四個性質或下面介紹的性質,對任何 階方陣
階方陣  都是成立的。
都是成立的。
性質五:若 包含一零列,則
包含一零列,則 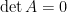 。
。
以二階行列式為例,利用性質三,將純量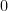 提出,就有
提出,就有

性質六:任一列乘以常數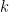 再加進另一列,行列式不改變。
再加進另一列,行列式不改變。
以二階行列式為例,若第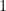 列乘以
列乘以 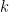 加進第
加進第 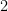 列,使用性質三和性質二,計算如下:
列,使用性質三和性質二,計算如下:
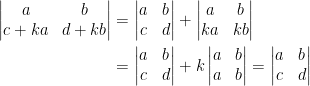
性質七:若 為三角形矩陣,
為三角形矩陣,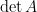 等於主對角元乘積。
等於主對角元乘積。
假設三角形矩陣![A=[a_{ij}] A=[a_{ij}]](https://s0.wp.com/latex.php?latex=A%3D%5Ba_%7Bij%7D%5D&bg=ffffff&fg=000000&s=0) 的主對角元皆不含零,以列取代運算將
的主對角元皆不含零,以列取代運算將  化簡為主對角矩陣,
化簡為主對角矩陣,
 性質六指出列取代運算不改變行列式,因此
性質六指出列取代運算不改變行列式,因此  。利用性質三,逐次將
。利用性質三,逐次將  的主對角元提出,再使用性質一,就有
的主對角元提出,再使用性質一,就有
性質八:若 是可逆矩陣,則
是可逆矩陣,則 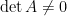 ;若
;若  是不可逆矩陣,則
是不可逆矩陣,則 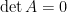 。
。
對矩陣 執行基本列運算,將
執行基本列運算,將  化簡為上三角形矩陣
化簡為上三角形矩陣 ![U=[u_{ij}] U=[u_{ij}]](https://s0.wp.com/latex.php?latex=U%3D%5Bu_%7Bij%7D%5D&bg=ffffff&fg=000000&s=0) ,性質四指出列交換運算改變行列式正負號,性質六則說明列取代運算不改變行列式,因此
,性質四指出列交換運算改變行列式正負號,性質六則說明列取代運算不改變行列式,因此 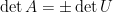 。再由性質七,
。再由性質七, ,推論當
,推論當  是可逆時,所有
是可逆時,所有  全不為零,故
全不為零,故 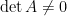 ;當
;當  不可逆時,
不可逆時,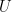 必有一零列,即至少有一
必有一零列,即至少有一 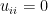 ,則
,則 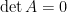 。
。
性質九:
這可能是最困難證明的一個性質,下面分開兩個情況討論。若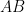 不可逆,則
不可逆,則  或
或 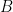 至少有一個是不可逆矩陣,性質八給出
至少有一個是不可逆矩陣,性質八給出 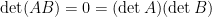 。若
。若  和
和 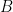 都是可逆矩陣,定義函數
都是可逆矩陣,定義函數
 函數
函數  滿足上述性質一、二和三,因此
滿足上述性質一、二和三,因此  。證明如下:設
。證明如下:設  ,
,
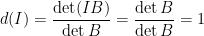 確定
確定  滿足性質一。若
滿足性質一。若 有相同兩列,則
有相同兩列,則 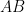 也有相同兩列,所以
也有相同兩列,所以 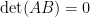 ,也就有
,也就有 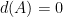 ,
, 滿足性質二。因為
滿足性質二。因為 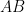 的第
的第 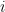 列等於
列等於  的第
的第 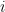 列乘以
列乘以 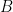 ,對於
,對於  的任一列的線性組合,
的任一列的線性組合,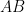 的該列也有同形式的線性組合,故
的該列也有同形式的線性組合,故  和
和 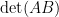 同為該列的線性函數,因此滿足性質三。(其他證明方式請見“利用分塊矩陣證明 det(AB)=(detA)(detB)”,“矩陣乘積行列式公式的代數證法”。)
同為該列的線性函數,因此滿足性質三。(其他證明方式請見“利用分塊矩陣證明 det(AB)=(detA)(detB)”,“矩陣乘積行列式公式的代數證法”。)
性質十:
如同性質九的證明,下面也分開兩個情況討論。若 不可逆,則
不可逆,則 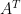 也不可逆,由性質八得知
也不可逆,由性質八得知 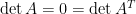 。若
。若  是可逆矩陣,考慮
是可逆矩陣,考慮  的 LU 分解 (見“LU 分解”),
的 LU 分解 (見“LU 分解”),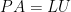 ,其中
,其中 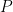 是排列矩陣,
是排列矩陣,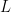 和
和 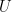 分別為下三角形和上三角形矩陣,且
分別為下三角形和上三角形矩陣,且 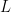 的主對角元全都是
的主對角元全都是 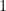 。利用性質九,
。利用性質九,
 對
對 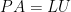 取轉置,得到
取轉置,得到 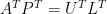 ,同樣根據性質九,
,同樣根據性質九,
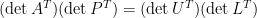 注意,三角形矩陣
注意,三角形矩陣 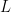 和
和 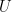 的轉置仍為三角形矩陣。由性質七,得知
的轉置仍為三角形矩陣。由性質七,得知  ,且
,且  。排列矩陣
。排列矩陣 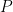 為正交矩陣,滿足
為正交矩陣,滿足  ,因此
,因此  。另外,
。另外,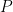 係由單位矩陣
係由單位矩陣 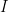 持續交換列而得,可知
持續交換列而得,可知 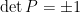 ,故
,故 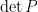 與
與 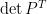 必同為
必同為 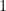 或
或 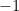 。綜合以上結果即證得
。綜合以上結果即證得  。
。
另一個證法採用基本矩陣 (elementary matrix) 分解。任一可逆矩陣 可分解為
可分解為 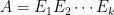 ,其中
,其中  ,
,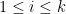 ,是基本矩陣。引用此性質:基本矩陣的轉置不改變行列式值,即
,是基本矩陣。引用此性質:基本矩陣的轉置不改變行列式值,即 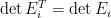 (見“特殊矩陣 (10):基本矩陣”)。因為
(見“特殊矩陣 (10):基本矩陣”)。因為  ,使用性質九,
,使用性質九,
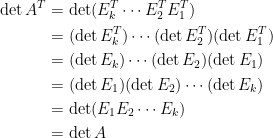
我們繼續推導高階行列式的運算方法及一般公式。性質七暗示一個行列式計算方法。對方陣 執行基本列運算,僅使用列交換和列取代運算可將
執行基本列運算,僅使用列交換和列取代運算可將  化簡為上三角形矩陣,因為列取代運算不改變行列式 (性質六),而列交換改變行列式的正負號 (性質四),根據性質七,即有下面的公式。
化簡為上三角形矩陣,因為列取代運算不改變行列式 (性質六),而列交換改變行列式的正負號 (性質四),根據性質七,即有下面的公式。
公式一:軸公式
設 為
為  階方陣,
階方陣,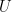 為基本列運算 (僅使用列交換和列取代) 化簡
為基本列運算 (僅使用列交換和列取代) 化簡  後得到的上三角形矩陣,
後得到的上三角形矩陣, 代表所執行的列交換次數,
代表所執行的列交換次數,
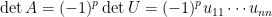 其中
其中 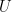 的非零主對角元
的非零主對角元  即為軸元 (pivot)。
即為軸元 (pivot)。
重複我們推導二階行列式的步驟可得三階行列式,總計分解為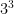 個行列式之和,但其中僅有
個行列式之和,但其中僅有  個非零行列式,如下:
個非零行列式,如下:
 每個組合行列式對應一排列矩陣
每個組合行列式對應一排列矩陣  ,
,  代表元
代表元 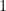 出現於元位置
出現於元位置 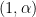 ,
, ,
, ,排列方式計有
,排列方式計有  種:
種:
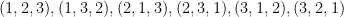 對單位矩陣
對單位矩陣 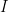 執行一序列的列交換即可得到排列矩陣
執行一序列的列交換即可得到排列矩陣  ,故
,故 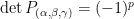 ,
, 表示從
表示從 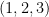 至
至  所執行的置換總數。所以,三階行列式公式為
所執行的置換總數。所以,三階行列式公式為
 下面是一般
下面是一般  階行列式公式。
階行列式公式。
公式二:排列公式 (或稱萊布尼茲公式)
上述三階行列式的任一列皆可作為因數提出,繼續代入二階公式,可得到一個僅含 個行列式的表達形式,以第
個行列式的表達形式,以第  列為例:
列為例:
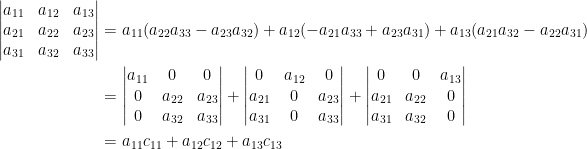 上式中,我們稱
上式中,我們稱 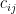 為餘因子 (cofactor),定義如下:
為餘因子 (cofactor),定義如下:
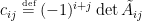 其中
其中  為移除
為移除  的第
的第 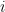 列與第
列與第 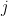 行後得到的
行後得到的  階子陣,
階子陣, 稱為餘子式 (minor)。這個運算公式稱為餘因子展開或 Laplace 展開公式。
稱為餘子式 (minor)。這個運算公式稱為餘因子展開或 Laplace 展開公式。
公式三:餘因子公式 (或稱 Laplace 公式)
設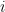 為任一列指標,
為任一列指標,
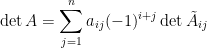
行列式的性質同時適用於列與行 (column)。如果將 定義為行向量
定義為行向量  和
和  所張的平行四邊形面積,只需要將以上討論的「列」改成「行」,並適當修改推導算式即可。另外,除了上述三個常見於教科書的行列式運算公式,還有兩個鮮為人知的運算法,有興趣進一步暸解的讀者請參閱“Chiò演算法──另類行列式計算法 ”和“Dodgson 縮合法──奇特的行列式運算法 ”。
所張的平行四邊形面積,只需要將以上討論的「列」改成「行」,並適當修改推導算式即可。另外,除了上述三個常見於教科書的行列式運算公式,還有兩個鮮為人知的運算法,有興趣進一步暸解的讀者請參閱“Chiò演算法──另類行列式計算法 ”和“Dodgson 縮合法──奇特的行列式運算法 ”。
向量积只存在于三维向量中? | 问答| 问答| 果壳网科技有意思在線性代數發展歷史中,行列式和矩陣理論一直有著密切的關係。行列式概念最早出現於解線性方程組的過程中,十七世紀末,日本數學家關孝和與德國數學家萊布尼茨 (Gottfried Wilhelm Leibniz) 的著作就已使用行列式來確定線性方程組解的個數以及形式[1]。十九世紀以後,矩陣的引入使得更多的行列式性質被發現,行列式的發展遂漸趨完善。今天多數線性代數教科書都會開闢一個專門討論行列式的章節,但主要的目的並非求解線性方程組,而是為了順利導入矩陣的特徵多項式。不過,美國數學教授阿斯勒 (Sheldon Axler) 卻抱持反對的態度,他認為行列式是線性代數核心原理的推導結果,而不是行列式推導出線性代數的核心原理。1994年,阿斯勒發表〈斷絕行列式〉 (Done with determinants!),該文嚴厲抨擊行列式目前於線性代數的「地位」,之後並獲得不少數學家的共鳴和迴響。阿斯勒反對行列式的理由在於行列式難以理解,不具直覺,而且常在缺乏明顯動機的情況下被引用。不僅如此,行列式和線性代數理論的基調不甚相合。行列式的計算公式與主要的矩陣運算無關,它像是從一堆矩陣元拼貼出來的蒙太奇,讓人困惑如此怪異的公式究竟是怎麼冒出來的。雖然我們無法改變或簡化行列式公式,但仍可嘗試編排出易於理解的推導過程。本文從一個簡單的面積計算問題推導行列式的運算公式,這麼做雖有違行列式誕生的初衷,但此法能夠豐富行列式的幾何直覺解釋並顯現行列式的一些重要性質。
設
首先考慮最簡單情況:
性質一:
再看另一個極端情況:
性質二:若
上述兩個性質仍不足以規範函數
從基礎幾何學可知
運用對稱原理,同樣也有
性質三:考慮
這裡要特別強調
如果將
性質四:交換
性質四迫使函數
準備就緒,現在我們可以利用上述性質推導
接著我們推導行列式的其他性質。不論前述的四個性質或下面介紹的性質,對任何
性質五:若
以二階行列式為例,利用性質三,將純量
性質六:任一列乘以常數
以二階行列式為例,若第
性質七:若
假設三角形矩陣
性質八:若
對矩陣
性質九:
這可能是最困難證明的一個性質,下面分開兩個情況討論。若
性質十:
如同性質九的證明,下面也分開兩個情況討論。若
另一個證法採用基本矩陣 (elementary matrix) 分解。任一可逆矩陣
我們繼續推導高階行列式的運算方法及一般公式。性質七暗示一個行列式計算方法。對方陣
公式一:軸公式
設
重複我們推導二階行列式的步驟可得三階行列式,總計分解為
公式二:排列公式 (或稱萊布尼茲公式)
上述三階行列式的任一列皆可作為因數提出,繼續代入二階公式,可得到一個僅含
公式三:餘因子公式 (或稱 Laplace 公式)
設
行列式的性質同時適用於列與行 (column)。如果將
www.guokr.com/question/510522/
轉為繁體網頁
轉為繁體網頁
为什么矩阵的行秩/列秩= 用秩一矩阵和逼近的最小项数 ... - 知乎
www.zhihu.com/question/25524419
轉為繁體網頁
轉為繁體網頁
三维空间已知张成一个平面的两个不平行向量,求法向量_百度知道
zhidao.baidu.com › 教育/科学 › 理工学科 › 数学
轉為繁體網頁
轉為繁體網頁
向量外积与行列式的本质关系| 数学笔记
math.tianpeng.org/2010/04/向量外积与行列式的本质关系/
轉為繁體網頁
轉為繁體網頁
【线性代数的几何意义】向量的基本几何意义- AndyJee - 博客园
www.cnblogs.com/AndyJee/p/3491458.html
轉為繁體網頁
轉為繁體網頁
[PDF]行列式几何化的教学研究
www.paper.edu.cn/index.../1674-5884(2012)04-0090-05
轉為繁體網頁
轉為繁體網頁
《线性代数》 - longhuihu的专栏- 博客频道- CSDN.NET
blog.csdn.net/longhuihu/article/category/1887589
轉為繁體網頁
轉為繁體網頁
[PDF]基于Clifford 代数的混合型传感器网络覆盖理论分析
info.scichina.com:8083/sciF/.../downloadArticleFile.do?...
轉為繁體網頁
轉為繁體網頁
何 ... 外积是一个二向量( 平面量) , 即这两个向量张成的平面内的. 一个有方向的面积 ...
向量外积与行列式的本质关系
在三维空间中,两个向量a和b的外积a×b定义为这样的一个向量:
1) |a×b|=|a||b|sin<a,b> 其中sin<a,b>表示a和b两向量夹角的正弦。
2) 若|a×b|≠0,那么a×b的方向垂直于a和b所在平面并且使a,b,c满足右手螺旋定则。
设i,j,k是三维空间中成右手定则关系的标准正交基底,a和b在这组基底下的坐标分别为(a1,a2,a3)和(b1,b2,b3),那么a×b可以用行列式形式地表示为
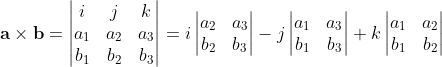
这个公式的由来,在一般的教材中,是先推导出外积的几个重要性质:
1) a×b = -b×a
2) (a+b)×c = a×c+b×c
3) a×(b+c) = a×b+a×c
4) a×(kb)=(ka)×b=k(a×b)
5) i×j=k,j×k=i,k×i=j
然后,就可以利用这些性质对以下式子进行展开:
a×b=(a 1 i+a 2 j+a 3 k)×(b 1 i+b 2 j+b 3 k)
最后化为上面的行列式表示。
但是,为什么外积可以如此规整地表示为一个行列式?难道只是巧合吗?一定有某些内在的原因。
设
c=(∣ ∣ ∣ a 2 b 2 a 3 b 3 ∣ ∣ ∣ ,−∣ ∣ ∣ a 1 b 1 a 3 b 3 ∣ ∣ ∣ ,∣ ∣ ∣ a 1 b 1 a 2 b 2 ∣ ∣ ∣ )
首先,注意到 c 的三个分量是那个三阶行列式中的三个子式,利用行列式展开法则,我们可以很容易地证明c垂直于a和b:
c⋅a =a 1 ∣ ∣ ∣ a 2 b 2 a 3 b 3 ∣ ∣ ∣ −a 2 ∣ ∣ ∣ a 1 b 1 a 3 b 3 ∣ ∣ ∣ +a 3 ∣ ∣ ∣ a 1 b 1 a 2 b 2 ∣ ∣ ∣ =∣ ∣ ∣ ∣ a 1 a 1 b 1 a 2 a 2 b 2 a 3 a 3 b 3 ∣ ∣ ∣ ∣ =0
c⋅b =b 1 ∣ ∣ ∣ a 2 b 2 a 3 b 3 ∣ ∣ ∣ −b 2 ∣ ∣ ∣ a 1 b 1 a 3 b 3 ∣ ∣ ∣ +b 3 ∣ ∣ ∣ a 1 b 1 a 2 b 2 ∣ ∣ ∣ =∣ ∣ ∣ ∣ b 1 a 1 b 1 b 2 a 2 b 2 b 3 a 3 b 3 ∣ ∣ ∣ ∣ =0
那么,为了证明c就是a×b,我们还需证明 |c|=|a||b|sin<a,b> ,以及a,b,c满足右手螺旋定则。
为了证明三个向量a=(a1,a2,a3),b=(b1,b2,b3),c=(c1,c2,c3)满足右手螺旋定则,只需验证行列式
| a1 a2 a3 |
| b1 b2 b3 |
| c1 c2 c3 |
的值是非负的。为此,我们将c的坐标代入,并把此行列式按c的那一行展开,得到行列式的值等于 |c| ² ,因此它确实是非负的。
下面证明|c|=|a||b|sin<a,b> 。考虑行列式
| a1 a2 a3 |
| b1 b2 b3 |
| c1 c2 c3 |
的几何意义,知道它是a,b,c三个向量组成的平行六面体的体积,前面我们已经知道它的数值等于 |c| ² 。又因为c垂直于a和b,那么下面的式子是成立的:
|c| ² =|a| |b| sin<a,b> |c| (因为体积等于底面积乘以高)
当c≠0时,我们直接可以得到 |c| =|a| |b| sin<a,b>。
当c=0时,我们任意取一个三维向量d=(d1,d2,d3),考虑行列式
| a1 a2 a3 |
| b1 b2 b3 |
| d1 d2 d3 |
因为它总是0,即不论d是什么向量,a,b,d总是线性相关。我们可以断定a,b线性相关,从而|a| |b| sin<a,b>=0,同样有|c| =|a| |b| sin<a,b>。
这样,没有用到外积的那些难以推导的性质,直接用行列式的性质,我们就证明了上面的外积表达式,而且这个证明更能揭示它们之间的本质联系。
因为有这样的本质联系,我们可以把三维空间中两个向量的外积推广到n维空间中的n-1个向量的情形。但是需要注意的是向量的顺序与定向的问题:如果规定
a1,a2, ...,an-1,a1×a2×...an-1取正向,那么必须在表示外积的行列式中把基底那一行写在最下面,然后按照基底那一行展开成各个分量。
在初级线性代数中,有几个概念之间有密切联系,这些概念是:
1)行列式,2)3个向量张成多面体的有向体积,3)2个向量的外积,4)3个向量的混合积
其实1,2,4直接相等,证明的途径多种多样,这里列出了一种,与一般的教科书稍有不同,即先承认1)等于2),再由此推出3)的表达式,最后推得4)等于1)。
其实承认1)等于2)之后,4)等于1)是很自然的(根据外积和混合积的定义),然后用类似上文的方法也可以推出3)的表达式。
如果开始像一般的线性代数书那样推导3)的表达式,那么4)等于1)就是显然的,从而可以证明1)等于2)。
这些内容都可以向高维空间推广,这里就不赘述了。
1) |a×b|=|a||b|sin<a,b> 其中sin<a,b>表示a和b两向量夹角的正弦。
2) 若|a×b|≠0,那么a×b的方向垂直于a和b所在平面并且使a,b,c满足右手螺旋定则。
设i,j,k是三维空间中成右手定则关系的标准正交基底,a和b在这组基底下的坐标分别为(a1,a2,a3)和(b1,b2,b3),那么a×b可以用行列式形式地表示为
这个公式的由来,在一般的教材中,是先推导出外积的几个重要性质:
1) a×b = -b×a
2) (a+b)×c = a×c+b×c
3) a×(b+c) = a×b+a×c
4) a×(kb)=(ka)×b=k(a×b)
5) i×j=k,j×k=i,k×i=j
然后,就可以利用这些性质对以下式子进行展开:
最后化为上面的行列式表示。
但是,为什么外积可以如此规整地表示为一个行列式?难道只是巧合吗?一定有某些内在的原因。
设
首先,注意到 c 的三个分量是那个三阶行列式中的三个子式,利用行列式展开法则,我们可以很容易地证明c垂直于a和b:
那么,为了证明c就是a×b,我们还需证明 |c|=|a||b|sin<a,b> ,以及a,b,c满足右手螺旋定则。
为了证明三个向量a=(a1,a2,a3),b=(b1,b2,b3),c=(c1,c2,c3)满足右手螺旋定则,只需验证行列式
| a1 a2 a3 |
| b1 b2 b3 |
| c1 c2 c3 |
的值是非负的。为此,我们将c的坐标代入,并把此行列式按c的那一行展开,得到行列式的值等于 |c| ² ,因此它确实是非负的。
下面证明|c|=|a||b|sin<a,b> 。考虑行列式
| a1 a2 a3 |
| b1 b2 b3 |
| c1 c2 c3 |
的几何意义,知道它是a,b,c三个向量组成的平行六面体的体积,前面我们已经知道它的数值等于 |c| ² 。又因为c垂直于a和b,那么下面的式子是成立的:
|c| ² =|a| |b| sin<a,b> |c| (因为体积等于底面积乘以高)
当c≠0时,我们直接可以得到 |c| =|a| |b| sin<a,b>。
当c=0时,我们任意取一个三维向量d=(d1,d2,d3),考虑行列式
| a1 a2 a3 |
| b1 b2 b3 |
| d1 d2 d3 |
因为它总是0,即不论d是什么向量,a,b,d总是线性相关。我们可以断定a,b线性相关,从而|a| |b| sin<a,b>=0,同样有|c| =|a| |b| sin<a,b>。
这样,没有用到外积的那些难以推导的性质,直接用行列式的性质,我们就证明了上面的外积表达式,而且这个证明更能揭示它们之间的本质联系。
因为有这样的本质联系,我们可以把三维空间中两个向量的外积推广到n维空间中的n-1个向量的情形。但是需要注意的是向量的顺序与定向的问题:如果规定
a1,a2, ...,an-1,a1×a2×...an-1取正向,那么必须在表示外积的行列式中把基底那一行写在最下面,然后按照基底那一行展开成各个分量。
在初级线性代数中,有几个概念之间有密切联系,这些概念是:
1)行列式,2)3个向量张成多面体的有向体积,3)2个向量的外积,4)3个向量的混合积
其实1,2,4直接相等,证明的途径多种多样,这里列出了一种,与一般的教科书稍有不同,即先承认1)等于2),再由此推出3)的表达式,最后推得4)等于1)。
其实承认1)等于2)之后,4)等于1)是很自然的(根据外积和混合积的定义),然后用类似上文的方法也可以推出3)的表达式。
如果开始像一般的线性代数书那样推导3)的表达式,那么4)等于1)就是显然的,从而可以证明1)等于2)。
这些内容都可以向高维空间推广,这里就不赘述了。
外积典型的称呼张量积或有类似势的运算如楔积。这些运算的势是笛卡尔积的势。这个名字相对于内积,它是有相反次序的积。
平凡解是Ax=0中的零解,即x=0。中文名
平凡解外文名
Trivial Solution定 义
Ax=0中的零解,即x=0,称为平凡解应用学科
数学数学范畴
矩阵代数
矩阵代数的中的定义,因为任何线性空间的子空间都过零点, 所以明显的等于0的时候解是成立的,但这显然没什么意义,说这个0解是平凡的,通俗来讲,如果方程组AX=0, 只有当X=0的时候才成立,就说方程组AX=0只有平凡解(trivial solution),此时肯定有行列式|A| 不为零。相反如果方程组AX=0存在非零解,也就是说存在不为零的X也可以使方程组AX=0成立,则说方程组AX=0存在非平凡解(nontrivial solution),此时肯定有系数矩阵行列式的值|A|=0。向量积只存在于三维向量中?
初:
若向量a叉乘向量b得c,由向量积的性质,c是一个垂直于a,b的向量,则
1、若a,b是二维的,则(一般)不可能存在3个二维向量互相垂直
2、若a,b是四维或更高维的,则又至少有两个向量与a,b互相垂直
对于1,c是不可定义的,对于2,c得定义似乎是歧义的(?)
Q0. 所以,向量积只存在于三维向量中?
其实想起这个事是想用向量积算面积的,于是有下面的问题:
Q1. 对于两个n维向量,是否存在一个关于坐标的运算,其结果是这两向量所夹平行四边形的面积?或者类似于向量积,其结果是个向量而其模是面积?
自然的,三维里面还有个混合积的东西,这东西在高数书里使用行列式定义的,三个三维向量算行列式没问题,三个四维向量就bug了...于是有
Q2.对于三个n维向量,是否存在一个关于坐标的运算,其结果是这三个向量所夹平行六面体的体积?
类似的,可以发散成下面这个很泛化的问题
Q3. n维空间中的m个向量可唯一确定一个m维超"立方"体,如何通过这些向量的坐标计算超"立方"体的体积?(显然不一定立方,但也不知道怎么称呼...)
就这样嗯...1个答案假定你学过线性代数,不然没法讲……
向量积有很多名字,比如说叉积、外积。它的推广也有很多种。不过,要回答你这个问题,我们还是用外积这个名字吧。
为什么不用向量积这个名字呢?向量的模表示的是一个长度,两个向量的外积的模表示的却是一个面积。虽然我们习惯了,但细想起来这还是有点不自然的。而且,如果把两个向量的外积当作一个向量的话,这个向量是依赖于坐标系的。也就是说,它在坐标变换下不能保持不变。这实在不是什么好的性质。从物理学的角度来看,它们的量纲也是不同的。
也就是说,我们应该把它们区分开来看,把向量与向量的外积看成是不同的东西;至少看成是不同的空间中的向量。
那么,应该把向量的外积看作是什么东西呢?
考虑三维空间里的一组基
,它们对应于3条坐标轴。两个向量的外积是一个“面积向量”,于是可以想象,如果把全体“面积向量”组成的线性空间记作
的话,
的基底可以取成对应于3个坐标平面(对,恰好也是3个)。把这组基记为
。这里用了
这个符号,这是外代数里表示外积的符号,叫做wedge,是楔子的意思,因此外积也叫楔积。
为了方便,我们还可以增加一些约定。由一个向量和它自己张成的“平行四边形”(可以看成是退化的平行四边形)面积为0,于是可以约定
、
、
。另一方面,在考虑物理等实际问题的时候定向是很重要的,从正面看过去的“面积”和从反面看过来的“面积”可以看成是相反的,所以可以约定:
、
、
。
这样一来,我们已经定义好了对于三个基底这个
该怎么算。于是,很容易把这个
双线性地延拓成一个
的运算。
比如说,对于
和
,
就等于
有没有发现这有结果看起来点熟悉?
如果把最后的
换成
,
换成
,
换成
,这就是我们熟悉的“向量积”了。
但我们不换。
对于面积,我们有了。于是很自然地想到,对于体积,我们也应该有个
。而且,它的一组基是
。也就是说,
是一个一维的向量空间。然后约定,对于
,如果调换其中两项,得到的就是原来的乘以-1,比如说
。这样,如果
中有两项是一样的,比如说
,那么调换这两项的次序,就有
,于是它只能等于0。
这样,和前面类似,我们就可以定义三个向量的外积了。经过验算(具体过程我就不写了)就会发现:三个向量的外积就是我们熟悉的混合积,当然还要乘上一个。
再看一遍前面的过程,就会发现“三”这个维数在这里并没有起到什么特别的作用,顶多是使得的维数和
恰好一样。于是,我们可以把这些东西推广到任意一个有限维的向量空间。也就是说,对一个
维的向量空间,取它的一组基
。这样,对
,就可以取
为由
张成的向量空间(这个空间是
维的)。然后约定,对
(这里不要求
),如果调换其中两项,得到的东西等于原来的乘以-1。然后就可以像前面那样那样定义
个
维向量的外积。然后,这个外积(在
这个
维空间中)的模就是你所问的那个“体积”了。特别地,在
的时候,
是个一维空间,
个
维向量正好可以排成一个
的方阵,这些向量外积正好相当于这个矩阵的行列式(具体的我也不算了)。
到目前为止已经回答了你的全部问题。
不过,中两个向量取了一下外积就到了
里,
中的东西再和
中的东西取外积又到了
里……这样总有点不方便。于是我们可以把它们统一一下。我们把实数域
当作一维的向量空间,就记作
,约定它和其他东西的外积就等于数乘。然后把
自己记作
。然后取所有这些
直和,得到
,记作
。它也是个向量空间。除了向量空间的结构,这个东西上面还有一个外积运算。我们把这个东西叫做外代数。
前面都是先选了上的一组基,然后才定义出这么一堆东西。其实它们的定义也可以不依赖于基的选取,不过要先讲张量什么的,我这里就不介绍了。
外代数还有个叫“泛性质”的性质(这段看不懂就算了):对任一个结合代数(这里说的“结合代数”指的是有某种形式的“乘法”运算,而且这个运算满足结合律的向量空间,下面就把这个“乘法”记作
)和任何一个线性映射
,如果对
中任一个元素
都有
,那么就有唯一的一个代数同态
,使得
,这里
是
到
的嵌入,也就是把
等同于
中的那个
。
当然,向量积还有别的一些推广,不过我不是很了解,就不说了。可以参考维基百科的Cross Product词条。我这里只举一个跟你的问题关系不是很大的小例子:
考虑三阶反对称矩阵(也就是满足的矩阵
)的全体
。这种矩阵一定长成
的形式,因此是一个三维的线性空间。然后在
上定义一种叫“李括号”的运算
。算算看,这样会得到什么东西?
就说这么多。不说了
矩阵的秩与行列式的意义_百度文库
wenku.baidu.com/view/5364a532eefdc8d376ee324c.html
轉為繁體網頁2012年11月11日 - 因此,我们可以将面积看成一个映射: 其中V 就是一个矢量,V*V 代表两个 ... 是X 和Y 轴上的单位正向量,那么由这两个矢量张成的四边形就是一个 ... 显然(两个共线矢量所张成的平行四边形还是一条线,因此面积为0): 假定面积映射是一个 .... 成的平行四边形,退化成一个线,其面积显然是0;一组共面的三个矢量张成 ...