| |
在幾何學的發展之中,有許許多多幾何學,像歐幾里得幾何學、投影幾何學……及其他種種幾何學,自然就要有一個人把它綜合集結起來,那就是德國的數學家克萊恩(F. Klein, 1849~1925年)。他在二十二歲的時候,前往德國小城 Erlangen 的一所大學任教。依據德國的習慣,新教授上任必須做一次公開演講,而他講演的結果──Erlangen program,就是這個新幾何學,他把幾何學建立在群的觀念上:一個空間有一個變換群,允許把空間的圖形從這個位置移到另一個位置。因此有了一個群之後,便有一種幾何,它研究所有經過這個變換群不變的幾何性質。這個群可以是歐幾里得運動群,也可以是投影變換群,或者其他種種的群。因為群的選擇不同,也就得到許多不同的幾何學;其中包括非歐幾何學。 仿克萊恩的觀點,只要在空間中有一個所謂二次的超曲面,就有一個非歐幾何,它討論使這個二次超曲面不變的投影變換子群所相應的幾何性質。如:在平面上有一個圓周,非歐幾何就變成研究圓內點所構成的空間的性質,也就是在雙曲平面 (hyperbolic plane) 上討論。因此由克萊恩的觀點,非歐幾何學就變得極易處理。 在這階段前,還有黎曼 (Riemann) 幾何的發展,這是笛卡兒坐標幾何的自然推廣。在笛卡兒坐標系中如果我們取 m 維的空間,一個點就可以用 m 個坐標 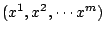 來表示,而此點到原點的距離如果是 d,那麼就有 來表示,而此點到原點的距離如果是 d,那麼就有 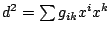 (見圖五)。即這個點到原點距離的平方,是坐標的一個二次式。而黎曼不但用坐標,他還用坐標的微分,於是硬把笛卡兒幾何局部化。因此黎曼幾何可說是一個局部化的幾何。黎曼幾何主要建構在弧長 s 上,弧長微分的平方會等於坐標的一個二次微分式,即 (見圖五)。即這個點到原點距離的平方,是坐標的一個二次式。而黎曼不但用坐標,他還用坐標的微分,於是硬把笛卡兒幾何局部化。因此黎曼幾何可說是一個局部化的幾何。黎曼幾何主要建構在弧長 s 上,弧長微分的平方會等於坐標的一個二次微分式,即 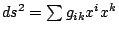 ;用弧長即可建立一個幾何,因為既然有了 ds,便可計算兩點所連接的曲線的長度,也就是弧長。「測地線」(geodesic) 是指在兩點間使弧長最短的那條曲線,它是平面上直線的推廣。有了測地線,便可以有面積及其他種種觀念。 ;用弧長即可建立一個幾何,因為既然有了 ds,便可計算兩點所連接的曲線的長度,也就是弧長。「測地線」(geodesic) 是指在兩點間使弧長最短的那條曲線,它是平面上直線的推廣。有了測地線,便可以有面積及其他種種觀念。
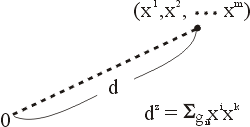
圖五 |
黎曼幾何最初在二維的情形是高斯(Gauss, 1777~1854年)發展的,他在1827年寫了一本差不多五十頁的小冊子,研究在二維(即曲面)的情形及這樣的 ds2 之下,所能夠發展的幾何性質。他的目的是為了應用,因為當時的德國 Hannover 政府要他主持一個測量工作,為了給這個測量工作一個理論甚礎,於是高斯寫下了這篇在微分幾何上最要緊的論文,微分幾何自此誕生。以前關於把微積分用在幾何上的問題,只能說是微積分在幾何學上的應用,在高斯這篇文章之後,微分幾何便成了一門獨立的學問,就是從 ds2 得到一切的幾何性質。 1854年,黎曼(1826~1866年)在為取得大學教書資格的公開演講上,發表了黎曼幾何的第一篇論文。黎曼幾何並不像其他我們所談的歐幾里得幾何,或者克萊恩的 Erlangen program 幾何,或者是投影幾何,需要整個的空間。在黎曼幾何的情形之下,我們只需要空間的一部分,因為 ds2 有意義,我們便可量弧長、面積、角度等幾何性質,不需要知道全部的空間。也就是說,在這樣的一個小塊裡,便可發展全部的幾何性質,這是黎曼幾何革命性的觀念,使幾何局部化,這個和物理上的場論是完全符合的。 真正使黎曼幾何受到重視的是愛因斯坦的廣義相對論。大致說起來,愛因斯坦的廣義相對論是要把物理幾何化,也就是說把物理的性質變為幾何的性質,因此黎曼幾何就成為物理學家一定要念的一門數學。到了黎曼空間一樣有曲率的概念,只是因為黎曼空間是高維的,所以它的曲率概念就變得相當複雜。在愛因斯坦的廣義相對論中的基本公式裡,大致說起來,物理的力是一個曲率;數學家講曲率和物理學家講力、位 (potential)、速度,是完全可以把它們連在一起的。
從歐幾里得到微分幾何
什麼是幾何學 (第 6 頁) 陳省身
整理:林麗明
| |
.原載於科學月刊第十八卷第六期
‧對外搜尋關鍵字 |
| |
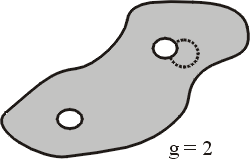
在黎曼幾何中,Levi-Civita 平行性是一個重要的觀念。Levi-Civita 以為在黎曼幾何(廣義相對論裡的其中一種,稱為勞倫茲幾何)都有一個很基本的性質,那就是平行性;在這個時候,空間不再是只用一個坐標系表示的空間,而是需要很多不同的坐標系才能表現的「流形」(manifold),這樣又把幾何研究的空間推廣了。所以我常有個比喻,如果我們把幾何空間的推廣和人類穿衣服的過程相對照,那麼一開始的歐幾里得幾何,便好比人在原始社會中沒有穿衣服,是裸體的;然後笛卡兒把坐標的概念加入了「赤裸」的空間,就好比人類開始穿衣服;而到了流形的階段,就好比現代人,不只穿一件衣服,還要常常換。也許有些人不太能接受這樣「奇裝異服」式的換坐標,但是沒有關係,愛因斯坦花了七年的時間,才終於接受坐標可以轉換的概念,而能從狹義相對論進展到廣義相對論。空間中有不同的坐標系,那麼麻煩就來了,因為幾何的性質是和坐標系的選取有關,不過不要緊,只要我們能控制坐標變換的性質,使在變換前即有的性質,經過變換之後仍為我們所控制,那麼換坐標就沒關係了,這是近代幾何學比較困難的地方。 用以表示流形的坐標系是任意的,因此可能是非線性的坐標,這在處理上就變得比較困難;但是我們可以取線性的空間去逼近流形。換句話說,雖然流形本身是非線性的,但在流形上的一點,都有一個和普通空間一樣的線性空間,即切空間。這些切空間之間原本是沒有關係的,而 Levi-Civita 平行性就是要建立二點之間的切空間的關係;之後,微分幾何學家發現,這個平行性是非常基本的性質。又因為拓樸學 (topology) 的發展,我們把這個觀念推廣了,不一定要談切空間,任意一個空間都可以,於是就有矢量叢 (vector bundles) 和聯絡 (connections) 的觀念。也就是說流形的切空間差不多是平的,但是矢量叢卻可以是一個豎起來的空間,任何的矢量空間都可以,這是今天在幾何上大家所公認的一個基本結構。從黎曼幾何推廣到有聯絡的矢量叢,這也就是物理上規範場論 (gauge field) 的數學基礎。
從歐幾里得到微分幾何
什麼是幾何學 (第 7 頁) 陳省身
整理:林麗明
| |
.原載於科學月刊第十八卷第六期
‧對外搜尋關鍵字 |
|
|
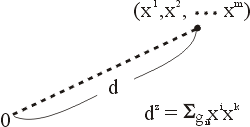
No comments:
Post a Comment