在标准状况下（或更一般地，等温等压的状况下），存在一个一般规律：
“
任何一个封闭系统都尽量使自由能最小。
”
因此，根据这个自然界的基本趋势，如果对于一个潜在反应，距离这个最小值进行定量测量，当热力学的计算显示吉布斯自由能ΔG的变化是负值的时候。本质上，这表明了那样一个反应更容易发生并且将释放能量。释放的能量等于这个化学反应所能够做的最大的功。相反，如果ΔG为正值，能量必须通过做功的方式进入反应系统使得此反应能够进行。
吉布斯自由能的物理含义是在等温等压过程中，除体积变化所做的功以外，从系统所能获得的最大功。换句话说，在等温等压过程中，除体积变化所做的功以外，系统对外界所做的功只能等于或者小于吉布斯自由能的减小。
“
任何一个封闭系统都尽量使自由能最小。
”
化学势和生成吉布斯自由能间的关系？
一般查热力学手册得到的都是标准摩尔生成吉布斯自由能。请问化学势和生成吉布斯自由能是一回事吗？是不是等温等压条件下化学势即为摩尔生成吉布斯自由能？
如果不是，请问怎么能计算得到非标准状态下的生成吉布斯自由能？
望相互交流，多多指教。
如果不是，请问怎么能计算得到非标准状态下的生成吉布斯自由能？
望相互交流，多多指教。
没人感兴趣吗？自己来顶一下吧。等温等压情况下有一反应，我不清楚式1和式2是否是等价的。从热力学手册上查到的数据应该为反应吉布斯自由能，但是对于非标准状态下的反应吉布斯自由能怎么求？若反应吉布斯自由能和化学势是相等的，则是否可以通过式3来求非标准状态下的化学反应自由能？
式1.jpg
式2.jpg
式3.jpg
式1.jpg
式2.jpg
式3.jpg
不是一回事, 举个例子,你有米缸,里面装了h高的米,由于重力,其具有能量E1,如果你再加一点米,能量就会增加E2,E2/米的量,随着增加的米的数量的减小而趋近于常数,这个常数就是化学位,而E1就是自由能.
忘了说了E2与高度h是有关系的
化学势是偏摩尔自由能。。。
未命名.JPG(34.14KB)
http://kuai.xunlei.com/d/LnU4DZrboV7pUAQA432?p=130497
未命名.JPG(34.14KB)
http://kuai.xunlei.com/d/LnU4DZrboV7pUAQA432?p=130497
化学势是偏摩尔自由能。。。
未命名.JPG(34.14KB)
http://kuai.xunlei.com/d/LnU4DZrboV7pUAQA432?p=130497
未命名.JPG(34.14KB)
http://kuai.xunlei.com/d/LnU4DZrboV7pUAQA432?p=130497
3楼: Originally posted by digghost at 2013-01-06 11:07:26
不是一回事, 举个例子,你有米缸,里面装了h高的米,由于重力,其具有能量E1,如果你再加一点米,能量就会增加E2,E2/米的量,随着增加的米的数量的减小而趋近于常数,这个常数就是化学位,而E1就是自由能.
你比喻的很形象，化学势随着物质的量的变化而变化的。我疏忽了，我想问的是标准态化学势和标准生成吉布斯自由能是否相等？查表得到的标准生成吉布斯自由能怎么换算成非一个大气压下的生成吉布斯自由能？不是一回事, 举个例子,你有米缸,里面装了h高的米,由于重力,其具有能量E1,如果你再加一点米,能量就会增加E2,E2/米的量,随着增加的米的数量的减小而趋近于常数,这个常数就是化学位,而E1就是自由能.
你的问题相当于气压，温度，体积对自由能的影响。如果是理想气体，这就好办了，用基本热力学方程就可以换算，如果是其他的体系，则根据自由能模型来讨论。这有很多模型。规则溶体，规则界面，居于浓度模型。。。。
在标准状况下（或更一般地，等温等压的状况下），存在一个一般规律：
因此，根据这个自然界的基本趋势，如果对于一个潜在反应，距离这个最小值进行定量测量，当热力学的计算显示吉布斯自由能ΔG的变化是负值的时候。本质上，这表明了那样一个反应更容易发生并且将释放能量。释放的能量等于这个化学反应所能够做的最大的功。相反，如果ΔG为正值，能量必须通过做功的方式进入反应系统使得此反应能够进行。
吉布斯自由能的物理含义是在等温等压过程中，除体积变化所做的功以外，从系统所能获得的最大功。换句话说，在等温等压过程中，除体积变化所做的功以外，系统对外界所做的功只能等于或者小于吉布斯自由能的减小。数学表示是：
，上式化为：
特别地，吉布斯自由能是一个广延量，单位摩尔物质的吉布斯自由能就是化学势
，也就是说。
，代入热力学第一定律的微分形式：
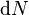。这时，
,
,
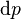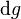这些强度量的变化为零。所以必然有
，
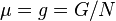表示。
通过生成吉布斯自由能，我们能算出标准反应自由能。标准反应自由能是指在标准状况下，标况下的反应物生成标况下的生成物所需要的能量变化，即用生成物的生成吉布斯自由能与各自的化学计量系数相乘后减去的反应物的生成吉布斯自由能与各自的化学计量系数相乘后的乘积。常用符号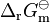
表示。
对于一般反应：
它的标准反应自由能![\Delta_\mathrm{r} G^\ominus_\mathrm{m} = [c \Delta_\mathrm{f}G^\ominus_\mathrm{m}(\mathrm{C})+ d\Delta_\mathrm{f}G^\ominus_\mathrm{m}(\mathrm{D})] - [a\Delta_\mathrm{f}G^\ominus_\mathrm{m}(\mathrm{A})+ b\Delta_\mathrm{f}G^\ominus_\mathrm{m}(\mathrm{B})]](http://upload.wikimedia.org/math/f/1/8/f182c2ef1ed9011926cc3b0196e15ea1.png)
一般化学教科书和化学手册中都列出常见物质的生成吉布斯自由能（同时还会列出生成焓和标准熵），用时直接查表便可。
在标准状况下（或更一般地，等温等压的状况下），存在一个一般规律：
“
任何一个封闭系统都尽量使自由能最小。
”
吉布斯自由能的物理含义是在等温等压过程中，除体积变化所做的功以外，从系统所能获得的最大功。换句话说，在等温等压过程中，除体积变化所做的功以外，系统对外界所做的功只能等于或者小于吉布斯自由能的减小。数学表示是：
，上式化为：
特别地，吉布斯自由能是一个广延量，单位摩尔物质的吉布斯自由能就是化学势
，也就是说。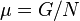
，
，代入热力学第一定律的微分形式：
，
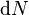。这时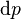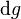，,,这些强度量的变化为零。所以必然有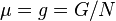，生成吉布斯自由能[编辑]
由于自由能的绝对值很难求出，同时它又是一个状态函数，所以实际应用时，就采用各种物质与稳定单质的相对值，即生成吉布斯自由能，全称标准摩尔生成吉布斯自由能变。它是由处于标准状况下的稳定单质生成一摩尔标准状况下的化合物的吉布斯自由能变，用符号
表示。通过生成吉布斯自由能，我们能算出标准反应自由能。标准反应自由能是指在标准状况下，标况下的反应物生成标况下的生成物所需要的能量变化，即用生成物的生成吉布斯自由能与各自的化学计量系数相乘后减去的反应物的生成吉布斯自由能与各自的化学计量系数相乘后的乘积。常用符号
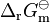表示。对于一般反应：
它的标准反应自由能
一般化学教科书和化学手册中都列出常见物质的生成吉布斯自由能（同时还会列出生成焓和标准熵），用时直接查表便可。
No comments:
Post a Comment