我们先引入一个粗粒(coarse-grained)序参量密度函数 ,我们可以把它看作原子大小尺度a范围内的平均磁距密度,因此 在比a更小的尺度里没有涨落。
[PDF]第八章: 相变与临界现象的基本概念
staff.ustc.edu.cn/~chenzyn/lectures/chapter8.pdf
轉為繁體網頁
说明低温下理想费米气体的亥姆霍茨自由能(A=U-TS)可表达为: 这里N是 ... 称破缺,
标签:
杂谈 |
反应焓变是包括体积变化做功的,只不过高中课不讲。吉布斯自由能减小只是表明反应发生在热力学上的可能性,表明这个反应不违反热力学定律,并不表示反应能发生,因为它还取决于动力学
大位能是統計力學中使用的一個量,特別是在開放系統的不可逆過程裡使用。
大位能被定義為
大位能的改變量為
當系統達到熱動力平衡,ΦG有最小值。可以由考慮到當定體積且溫度與化學位停止改變時dΦG為零而見到。
對於理想氣體,

這以羅斯物理學家列夫·朗道命名。取決於系統的規定,這可能是大位能的同義詞。
大位能是統計力學中使用的一個量,特別是在開放系統的不可逆過程裡使用。
大位能被定義為
大位能的改變量為
當系統達到熱動力平衡,ΦG有最小值。可以由考慮到當定體積且溫度與化學位停止改變時dΦG為零而見到。
對於理想氣體,
目录[隐藏] |
[编辑] 蘭道自由能
一些作者認為蘭道自由能或蘭道位能是[1][2]
這以羅斯物理學家列夫·朗道命名。取決於系統的規定,這可能是大位能的同義詞。



 ,這裡的F是亥姆霍茲自由能。對於齊次系統,可得
,這裡的F是亥姆霍茲自由能。對於齊次系統,可得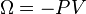
No comments:
Post a Comment