Thursday, April 23, 2015

DNA 幾何結構的基礎是微分幾何的曲線理論 White 的公式 Lk=Tk+W。兩個封閉曲線套起來的話有一個套數 Lk，它會等於 twist 和 writhingnumber 之和。套的數目可以很大很大， 可以使它套起來，也可以使它解開，恢復原來的形狀。

從歐幾里得到微分幾何
什麼是幾何學 （第 9 頁） 陳省身
整理：林麗明    
"三角形三內角之和等於180°，如果以弳(radian) 為單位，也可以說三角形三內角之和等於π."


[PPT]電腦輔助教學
web.thu.edu.tw/g922425/www/courseworks/g922425.ppt

三角形三內角之和等於180°，如果以弳(radian) 為單位，也可以說三角形三內角之和等於π. 內角A. 內角C. 內角B. 這本書在當時受到重視，不單只是為了學幾何，主要 ...
 
In physics, radiation is the emission or transmission of energy in the form of waves or particles through space or through a material medium. This includes ...

Radian - Wikipedia, the free encyclopedia

en.wikipedia.org/wiki/Radian

翻譯這個網頁
The radian is the standard unit of angular measure, used in many areas of mathematics. An angle's measurement in radians is numerically equal to the length of ...
‎Steradian - ‎Gradian - ‎Degree - ‎Radian (disambiguation)

  • Radians - Math is Fun

    www.mathsisfun.com/geometry/radians.html

    翻譯這個網頁
    Does 57.2958... degrees seem a strange value? Maybe degrees are strange, as the Radian is a pure measure based on the Radius of the circle: Radian: the ...

  • 「radian」的圖片搜尋結果檢舉圖片
    • radian的圖片搜尋結果
      {"id":"ij27HPf56nMtqM:","oh":300,"os":"34KB","ou":"http://upload.wikimedia.org/wikipedia/commons/thumb/9/9a/Degree-Radian_Conversion.svg/300px-Degree-Radian_Conversion.svg.png","ow":300,"pt":"Radian - Wikipedia, the free encyclopedia","rh":"en.wikipedia.org","ru":"http://en.wikipedia.org/wiki/Radian","s":"","th":93,"tu":"https://encrypted-tbn3.gstatic.com/images?q\u003dtbn:ANd9GcTP6Kzyr8UhZ5i_wdY9GRaLPwcbT_TR9hbMsJ5qVEmMtWt5joBMep9qnlI","tw":93}
    • radian的圖片搜尋結果
      {"id":"AIfsTNTGRtJ_3M:","oh":252,"os":"4KB","ou":"http://mathworld.wolfram.com/images/eps-gif/Radian_700.gif","ow":252,"pt":"Radian -- from Wolfram MathWorld","rh":"mathworld.wolfram.com","ru":"http://mathworld.wolfram.com/Radian.html","s":"","th":93,"tu":"https://encrypted-tbn0.gstatic.com/images?q\u003dtbn:ANd9GcTNht4oqkl6ThVcZU169Jo1fS6ng02hrCa2qrEJb8ye0r_Y5YjoeaRUjQ","tw":93}
    • radian的圖片搜尋結果
      {"cb":6,"cl":3,"cr":3,"id":"mEzizkxYUbFmaM:","oh":200,"os":"4KB","ou":"http://www.mathsisfun.com/geometry/images/radian-definition.gif","ow":340,"pt":"Radians","rh":"mathsisfun.com","ru":"http://www.mathsisfun.com/geometry/radians.html","s":"","th":90,"tu":"https://encrypted-tbn2.gstatic.com/images?q\u003dtbn:ANd9GcQvAKw94o9nXpz0qhK2XfNA9OxIklxh0g7ntmnSHOrjIQMSddJBIh0TWIM","tw":153}
    • radian的圖片搜尋結果
      {"id":"NZzqgzZnD5nn4M:","oh":2000,"os":"109KB","ou":"http://upload.wikimedia.org/wikipedia/commons/thumb/3/3d/Radian_cropped_color.svg/2000px-Radian_cropped_color.svg.png","ow":2000,"pt":"Radian - Simple English Wikipedia, the free encyclopedia","rh":"simple.wikipedia.org","ru":"http://simple.wikipedia.org/wiki/Radian","s":"","th":93,"tu":"https://encrypted-tbn2.gstatic.com/images?q\u003dtbn:ANd9GcSoiSK2rfgCZSW19fS_rcFDWpSw7TSYul_XAxK4cXrBEz81Z6gIVWEkv7Y","tw":93}
    • radian的圖片搜尋結果
      {"id":"6S1IeWzcYtiuUM:","oh":407,"os":"34KB","ou":"https://blogger.googleusercontent.com/img/b/R29vZ2xl/AVvXsEgtw5Nk2CjvXwy0SwUuDnzh6_naR3iJZw6QwsbrbpJEmf0rbwkXW5xhIIluqlWuFFbAyxWdXcoA5nEi38vvX9y9E9jcO6Jei88Xr9kFnBvqVqQ7XmRdO7K0EYiY8Yy-IG3pXSirxQ95ZL5i/s1600/0199210896.radian.1.jpg","ow":406,"pt":"Life with Advanced Function ♥: 4.1 Radian Measure","rh":"jaryntan.blogspot.com","ru":"http://jaryntan.blogspot.com/2011/09/41-radian-measure_21.html","s":"","th":94,"tu":"https://encrypted-tbn0.gstatic.com/images?q\u003dtbn:ANd9GcQIm8_aw8epG1gXkyKkMKuXyVGYgxTbH7SAVkWOadkbB5fsZ8Qxd1aAVQ","tw":94}
    更多符合「radian」的圖片

    • 從歐幾里得到微分幾何
    什麼是幾何學
    陳省身
    整理：林麗明
    		 

     
    幾何原本
    在差不多一百年前，幾何就是歐幾里得。他在公元前三百年左右寫了一部大書，中文叫做《幾何原本》。從這本書我們可以看出：在當時的社會，幾何並不被大家所注意，所以像歐幾里得這樣偉大的人，我們也不大知道他的生平。大致說起來，他是屬於西元前365～275年間的人物，這是大致算的時間，並不表示他活了90歲。 這本書是人類文化史上一部非常偉大、有意義的著作，它的主要結論有兩個：
    一.畢氏定理： 有一直角三角形 ABC，則長邊的平方會等於其他兩邊的平方和。 由幾何方面來說，如果我們在三邊上各作一個正方形， 那麼兩個小正方形的面積和就會等於大正方形的面積（見圖一）。

    圖一 c2=a2+b2


    二.三角形 三內角之和等於 180°，如果以弳 (radian) 為單位， 也可以說三角形三內角之和等於 π
    這本書在當時受到重視，不單只是為了學幾何，主要還要學一種邏輯推理的方法。歐幾里得用幾個很明顯的事實──公理，把幾何的結論從公理用邏輯的方法推出。而在他所列出的公理當中，較受爭議的是平行公理。平行公理原來是說：有兩條直線被一直線所截，如果截角的和小於 180°，那麼這兩條直線在充分延長後，必相交於一點。（見圖二）

    圖二 $\angle 1+\angle 2 < 180^{\circ} $

    另一個簡單的說法是：假使有一直線和線外一點， 那麼通過那個點就剛剛好只有一條直線和原來的直線平行。 平行者，就是這兩條直線不相交（見圖三）。

    圖三

    這個平行公理在所有公理之中是最不明顯的，所以數學家或是對數學有興趣的人便想從其他的公理去推得平行公理。而這努力延持了兩千年，後來證明這是不可能的，於是有了非歐幾何學的發現，這在人類思想史上是非常特別、有意思的事實。因此我感覺到這是西洋數學和中國數學不同的地方。 《九章算經》是中國古代最有名的數學書，一共九章，第九章談的是所謂勾股，勾、股就是直角三角形中較短約兩個邊，一個叫做勾，另一個就叫做股，而最長的那個邊便稱為弦。勾股定理也就是剛才所謂的畢氏定理，所以它的發現，中國人也應該有份。但是在中國的幾何中，我無法找到類似三角形三內角和等於 180° 推論，這是中國數學中沒有的結果。 因此，得之於國外數學的經驗和有機會看中國數學的書，我覺得中國數學都偏應用；講得過分一點，甚至可以說中國數學沒有純粹數學，都是應用數學。這是中國科學的一個缺點，這個缺點到現在還存在，大家都講應用，不注意基礎科學。當然應用很要緊，但是許多科學領域基本的發現都是在基礎科學。

    球面幾何與非歐幾何
    因為有三角形三內角之和等於 180° 這個結論，而有接下來的重要發展：
    一、球面幾何 球面幾何所討論的三角形，不一定是要在平面上，也可以是一個球面三角形，在這個情形下，三角形三內角之和會大於 180°，並且有一個非常重要的公式：

    \begin{displaymath}A+B+C-\pi = \frac{\mbox{{\fontfamily{cwM2}\fontseries{m}\sele... ....1pt{\fontfamily{cwM2}\fontseries{m}\selectfont \char 9}}}{R^2}\end{displaymath}


    R 是球的半徑，R2 則是度量球面的曲率，因此有曲率的觀念跑到這樣一個簡單的公式裡。這在數學或物理上是一個重要發展，因為愛因斯坦的相對論中，曲率＝ 1/R2 代表一個場的力，所以幾何度量和物理度量便完全一樣。
    二、非歐幾何 在這個情形下，三角形三內角之和是小於 180°的，即有如下的重要公式：

    \begin{displaymath}A+B+C-\pi = \frac{\mbox{{\fontfamily{cwM2}\fontseries{m}\sele... ....1pt{\fontfamily{cwM2}\fontseries{m}\selectfont \char 9}}}{R^2}\end{displaymath}


    此時 R2 代表非歐幾何的一個絕度的度量，換句話說在非歐幾何的平面上，它的曲率是負的，即 曲率＝ $- \frac{1}{R^2}$。因此，在空間或者平面的曲率，可以是正的，像球面幾何；也可以是負的，像非歐幾何。而其相對應的三角形三內角和，也分別有大於或小於 180°之情形，不再滿足歐幾里得的平行公理。
    		 
    ．原載於科學月刊第十八卷第六期
    ‧    對外搜尋關鍵字
     電腦輔助教學
    web.thu.edu.tw/g922425/www/courseworks/g922425.ppt

    三角形三內角之和等於180°，如果以弳(radian) 為單位，也可以說三角形三內角之和等於π. 內角A. 內角C. 內角B. 這本書在當時受到重視，不單只是為了學幾何，主要 ...

  • 三角形內角問題- Yahoo!奇摩知識+

    https://tw.knowledge.yahoo.com/question/question?qid=1609090708558

    因為有三角形三內角之和等於180° 這個結論，而有接下來的重要發展： 一、球面幾何球面幾何所討論的 ... A＋B＋C－π＝面積/R^2. R 是球的半徑，R2 則是度量球面 ... 在歐式幾何中三角形內角和為180度，而雙曲與橢圓幾何分別是不足與超過180度。

  • 特殊直角三角形- 維基百科，自由的百科全書 - Wikipedia

    zh.wikipedia.org/zh-hk/特殊直角三角形

    例如有些三角形的內角有一些簡單的關係，例如45–45–90度三角形，這是各角有特殊關係 ... 繪製一條對角線會產生一個角度比例為1 : 1 : 2的三角形，而內角和為180度（或是π弧度）， ... 若三角形各角的比例是1 : 2 : 3，其各角角度會是30°、60°和90°。

  • 從歐幾里得到微分幾何(第2 頁)

    episte.math.ntu.edu.tw/articles/sm/sm_18_06_1/page2.html

    2002年2月17日 - 一、球面幾何球面幾何所討論的三角形，不一定是要在平面上，也可以是一個球面三角形，在這個情形下，三角形三內角之和會大於180°，並且有一個 ...

  • 球面三角学_百度文库

    wenku.baidu.com/view/a82eecd789eb172ded63b711.html
    2013年5月25日 - 要注意的是，这些角都必须用径度量来量度（苏注：“π ”在数学中有两个含义：一表示圆周率3.14。二表示角度中的180 度。 .... 在平面幾何中，一個三角形的三個內角和恆等于一個平角，這是邏輯等價于平行公理的基本 ... 在球面三角形的情形下，三內角之和則恆大于一個平角，而下述[定理7.1]証明在單位球面上的球面 ...

  • [PDF]to download the PDF file. - 中研院數學研究所

    w3.math.sinica.edu.tw/math_media/d382/38206.pdf

    不一定正確, 例如球面幾何, 其三角形的三內角和大於180 度, 而非歐幾何或雙曲幾何則 ... 由曲面的一般理論知, 這三角形的三內角和減掉一個π 會跟曲面的曲率有關。

  • 歷史著名科學家@ 168 Shih's Blog. :: 隨意窩Xuite日誌

    blog.xuite.net/strong98009/twblog1/178250438-歷史著名科學家

    證明了三角形的內角和為180度。 2. 已知有正四面、 .... 三角形三內角之和等於180°，如果以弳(radian) 為單位， 也可以說三角形三內角之和等於π. 這本書在當時受到 ...

  • [FLASH]八年級數學 - 後壁國中

    www.hbjh.tn.edu.tw/102-2/math2.swf
    十七）能了解圓心角θ度的扇形面積為「半徑‧半徑‧π‧ （θ÷360）」。 ... 三十一）能從三角形內角和為180度及一個內角與其外角和等於180度，推得外角等於兩個內對角的和 ...

  • 爲什麽三角形內角之和總等于180度？ - 王朝網路- wangchao ...

    tc.wangchao.net.cn › 信息

    數學上把確認三角形內角之和等于180度的幾何叫做“歐幾裏的幾何”，簡稱“歐氏幾何” ... 舉個例子,比如讓你證明2+1=3,你會說因爲1+1=2,所以2+1=1+1+1=3.那我問你 ...

  • Re: [中學] 如何正確的學習高中數學呢？ - 批踢踢實業坊

    https://www.ptt.cc/bbs/Math/M.1317735759.A.918.html

    2011年10月4日 - 3 篇文章 - ‎2 位作者
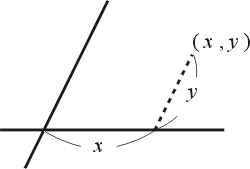
    例題1.cos15度,sin105度,tan75度練習2(2)sin68度cos23度-sin23度cos68度 ... 題目有提到三角形就會用到三內角和為180度,這類題目先給兩個角的三角函數 ... 度這也是基礎題都是將不是特別角的換成特別角2. 例題3.(2)α+β=π/4，

    •  


    坐標幾何
    歐幾里得幾何之後，第二個重要的發展是坐標幾何。這是法國哲學家、數學家笛卡兒（1596～1650年），對於研究幾何，引進了坐標的概念，因此可用解析的方法來處理幾何的問題。坐標就是說：假使在 X-Y 平面上，有兩個軸：X 軸和 Y 軸，那麼一個點的兩個 X、Y 坐標，就分別以如圖四中的兩個相對應的度量來表示。

    圖四

    因此幾何的討論可用解析方法，即：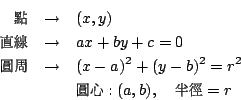

    \begin{eqnarray*} \mbox{{\fontfamily{cwM2}\fontseries{m}\selectfont \char 245}} ... ...s0.1pt{\fontfamily{cwM5}\fontseries{m}\selectfont \char 16}} = r \end{eqnarray*}


    於是幾何的問題便成為代數的問題。
    這樣的發展不但使幾何問題的處理容易些，更有其重大的意義：
    一、解析之後，使可研究的圖形的範圍擴大，除了直線的一次方程式， 或者圓周的二次方程式，我們還可以取任意的方程式 f(x,y)=0， 討論所有點它的坐標 (x,y) 適合這樣方程式的軌跡。 因此許多用幾何的方法很難處理的曲線，在解析化之後， 都可從表示它的方程式中得到有關的幾何性質。
    二、研究的圖形不再局限在二維的平面上，可推廣至高維的空間。 世界上的事情，如果只用二維的平面，往往不足以表示， 需要取更多的坐標。例如我們所在的空間是三維，有 x、y、z 三個度量。 假使要用幾何來表示物理的問題，那麼三個度量之外，尚須加一個時間 t， 所以物理的空間就變成了四維的空間；不但如此，假使有一點在三維空間運動，那麼除了需要 (x,y,z) 來表示點的位置， 還需要這三坐標對時間的微分來表示它的速率， 即 ( $\frac{dx}{dt} ,\frac{dy}{dt}, \frac{dz}{dt}$)， 這就成了六維空間。所以種種的情形都指示我們有必要考慮更高維的空間， 來表示自然的現象。 解析幾何把幾何研究的範圍大大地擴大了，而科學發展的基本現象， 就是要擴大研究的範圍，了解更多的情形。笛卡兒的解析幾何， 便達到了這個目的，使幾何學邁入一個新的階段。
     
    從歐幾里得到微分幾何
    什麼是幾何學     （第 4 頁） 陳省身
    整理：林麗明
    		 
    ．原載於科學月刊第十八卷第六期
    ‧    對外搜尋關鍵字

     
    群的觀念
    第三個發展是群的觀念，這是數學上一個基本的結構。數學上總是要運算，加、減、乘、除；研究幾何的話，把這個東西從這個位置移動到其他的位置，也是個運算。而這樣的運算（也稱為運動）有一個特別的性質，也就是說：把一個物體從甲地移到乙地，再移到丙地，可直接把物體從甲地移到丙地，即兩個運動的結果，可經由一次運動來達成，具有這個特殊性質的，便稱其成一群。研究幾何的對象，應是研究經運動群後是不變的幾何的性質。這個觀念立刻便有了重要的發展。 既然討論運動群，有時我們還想討論更大的群，看是不是有些性質不但在運動群下不變，在更大的群之下也是不變。歷史上最主要的例子是投影。假使兩條直線在空間中相交，從一點投影，被一新平面所截，則所得之二直線仍舊是相交。這種「直線相交」的幾何性質，是經過一種比運動還廣的投影之後，仍然不變的。這也有許多應用，如藝術家畫畫，講求透視，遠近合乎幾何的條件。 研究幾何性質在投影群之下不變的是所謂投影幾何。投影幾何的發展，把幾何的觀念推廣了，不只是有普通的歐幾里得幾何（討論幾何性質經運動群後不變的），也可以討論投影幾何中，投影後仍是不變的性質。有許多經運動群後不變的性質，在投影變換後是變了的，像距離、角度，但是還有些更重要的性質在投影下是不變的，而且這些性質能經過（大一點的）投影群不變，在幾何上自有其重要的意義。 法國數學家 Poncelet（1788～1867年），在投影幾何發展史上是一個主要的人物。他曾追隨拿破崙攻打俄國，被俄俘擄，囚禁在俄國監獄中，而他的主要著作，也就是在此時完成的。因此，大家常常抱怨科學研究的設備不好，相形之下，這個例子可以證明這不是科學研究最主要的問題──當然這情形非常例外。


    什麼是幾何學 （第 5 頁） 陳省身
    整理：林麗明
    		 
    ．原載於科學月刊第十八卷第六期
    ‧    對外搜尋關鍵字

     
    黎曼及克萊恩的幾何學
    在幾何學的發展之中，有許許多多幾何學，像歐幾里得幾何學、投影幾何學……及其他種種幾何學，自然就要有一個人把它綜合集結起來，那就是德國的數學家克萊恩（F. Klein, 1849～1925年）。他在二十二歲的時候，前往德國小城 Erlangen 的一所大學任教。依據德國的習慣，新教授上任必須做一次公開演講，而他講演的結果──Erlangen program，就是這個新幾何學，他把幾何學建立在群的觀念上：一個空間有一個變換群，允許把空間的圖形從這個位置移到另一個位置。因此有了一個群之後，便有一種幾何，它研究所有經過這個變換群不變的幾何性質。這個群可以是歐幾里得運動群，也可以是投影變換群，或者其他種種的群。因為群的選擇不同，也就得到許多不同的幾何學；其中包括非歐幾何學。 仿克萊恩的觀點，只要在空間中有一個所謂二次的超曲面，就有一個非歐幾何，它討論使這個二次超曲面不變的投影變換子群所相應的幾何性質。如：在平面上有一個圓周，非歐幾何就變成研究圓內點所構成的空間的性質，也就是在雙曲平面 (hyperbolic plane) 上討論。因此由克萊恩的觀點，非歐幾何學就變得極易處理。 在這階段前，還有黎曼 (Riemann) 幾何的發展，這是笛卡兒坐標幾何的自然推廣。在笛卡兒坐標系中如果我們取 m 維的空間，一個點就可以用 m 個坐標 $(x^1,x^2,\cdots x^m)$ 來表示，而此點到原點的距離如果是 d，那麼就有 $d^2= \sum g_{ik}x^ix^k$（見圖五）。即這個點到原點距離的平方，是坐標的一個二次式。而黎曼不但用坐標，他還用坐標的微分，於是硬把笛卡兒幾何局部化。因此黎曼幾何可說是一個局部化的幾何。黎曼幾何主要建構在弧長 s 上，弧長微分的平方會等於坐標的一個二次微分式，即 $ds^2 = \sum g_{ik}x^ix^k$；用弧長即可建立一個幾何，因為既然有了 ds，便可計算兩點所連接的曲線的長度，也就是弧長。「測地線」(geodesic) 是指在兩點間使弧長最短的那條曲線，它是平面上直線的推廣。有了測地線，便可以有面積及其他種種觀念。

    圖五

    黎曼幾何最初在二維的情形是高斯（Gauss, 1777～1854年）發展的，他在1827年寫了一本差不多五十頁的小冊子，研究在二維（即曲面）的情形及這樣的 ds2 之下，所能夠發展的幾何性質。他的目的是為了應用，因為當時的德國 Hannover 政府要他主持一個測量工作，為了給這個測量工作一個理論甚礎，於是高斯寫下了這篇在微分幾何上最要緊的論文，微分幾何自此誕生。以前關於把微積分用在幾何上的問題，只能說是微積分在幾何學上的應用，在高斯這篇文章之後，微分幾何便成了一門獨立的學問，就是從 ds2 得到一切的幾何性質。 1854年，黎曼（1826～1866年）在為取得大學教書資格的公開演講上，發表了黎曼幾何的第一篇論文。黎曼幾何並不像其他我們所談的歐幾里得幾何，或者克萊恩的 Erlangen program 幾何，或者是投影幾何，需要整個的空間。在黎曼幾何的情形之下，我們只需要空間的一部分，因為 ds2 有意義，我們便可量弧長、面積、角度等幾何性質，不需要知道全部的空間。也就是說，在這樣的一個小塊裡，便可發展全部的幾何性質，這是黎曼幾何革命性的觀念，使幾何局部化，這個和物理上的場論是完全符合的。 真正使黎曼幾何受到重視的是愛因斯坦的廣義相對論。大致說起來，愛因斯坦的廣義相對論是要把物理幾何化，也就是說把物理的性質變為幾何的性質，因此黎曼幾何就成為物理學家一定要念的一門數學。到了黎曼空間一樣有曲率的概念，只是因為黎曼空間是高維的，所以它的曲率概念就變得相當複雜。在愛因斯坦的廣義相對論中的基本公式裡，大致說起來，物理的力是一個曲率；數學家講曲率和物理學家講力、位 (potential)、速度，是完全可以把它們連在一起的。
    DNA 的基本公式
    最後談談 James White 的公式，這在分子生物學，DNA 方面是一個基本公式。DNA 在幾何上的結構是雙螺線，是兩條封閉的曲線互相繞著，所以很自然的，研究 DNA 幾何結構的基礎是很簡單的微分幾何的曲線理論，和剛剛談的結有關，即打了一個結，結的數學性質就對應到 DNA 的生物反應。目前王倬教授正在南港從事這方面的實驗。 DNA 分子雖是一個螺線，卻不像我們所想像的，它的螺線是以最經濟的方式互相纏繞，而產生了許多複雜而有意思的幾何問題。之中有一個就是 White 的公式：Lk=Tk+W。兩個封閉曲線套起來的話有一個套數 Lk，它會等於 twist 和 writhing-number 之和。套的數目可以很大很大，分子生物的現象，不僅是可以使它套起來，也可以使它解開，恢復原來的形狀。總而言之，我不懂這些生物學，只是道聽塗說。 大家覺得微分幾何應該是很有用的，因為在物理學發展之中，電磁學對人類日常生活是最有影響的；而在遺傳工程及其他方面，DNA 的結構也是生物科學對人類生活最有影響的一門學問。很巧，我剛好就是研究這兩門學問的數學基礎：微分幾何。這讓我聯想到一個有名的理論物理學家，E. Wigner 所寫的一篇文章：〈The unreasonable effectiveness of mathematics in science〉。為什麼數學會有用？光玩玩虧格、結，竟也能找到有用的數學性質，提供了很好的應用，他覺得很不可思議。在這篇文章的開頭，他舉了一個更簡單的例子：有兩個中學同學，畢業後各奔前程，若干年後，兩個人再度碰面，甲便問乙近幾年在研究什麼？乙說他在研究人口問題，甲便欣賞了一下乙的論文，發現論文裏頭總有個 π。我們都知道 π 是圓周率，怎麼可以和人口問題發生關係？這也是一個最粗淺的例子，告訴我們：基本的發現，有時候也不一定要求立刻的應用，可能結果有更大的應用。     		  

    這是 http://web.thu.edu.tw/g922425/www/courseworks/g922425.ppt 的 HTML 檔。
    G o o g l e 在網路漫遊時會自動將檔案轉換成 HTML 網頁。
    投影片 1

    主題：幾何圖形 
    單元：三角形


    幾何觀念的來源 
      根據希臘歷史學家希羅多德（Herodotus, 約西元前485～425年）的說法，幾何學開始於「測地」。古埃及的尼羅河每年氾濫，湮沒田地，因此需要重新測量土地。幾何學「Geometry」一詞就是由「Geometrein」演變而來的，其中「geo」是指土地，「metrein」是指測量。測量土地的技術員叫做操繩師 (rope-stretchers)，因為繩子是用來幫忙測量的工具。


      幾何觀念的第二個來源是航海與天文學。哲學家康德說： 
      有兩樣事物充滿著我的心，並且產生永不止息的敬畏。那就是：在頭上燦爛的星空，以及心中的道德法則。
      幾何學的第三個來源是日常生活的測積。由此引出了長度、面積、容積、體積、表面積、重心等概念，也歸結出一些計算公式。 


    歐幾里得的幾何原本  
      在差不多一百年前，幾何就是歐幾里得。他在公元前三百年左右寫了一部大書，中文叫做《幾何原本》。從這本書我們可以看出：在當時的社會，幾何並不被大家所注意，所以像歐幾里得這樣偉大的人，我們也不大知道他的生平。大致說起來，他是屬於西元前365～275年間的人物，這是大致算的時間，並不表示他活了90歲。


    這本書是人類文化史上一部非常偉大、有意義的著作，它的主要結論有兩個 
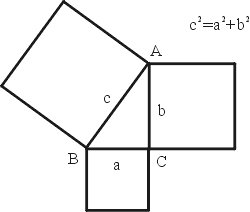
    一.畢氏定理：有一直角三角形  ABC，則長邊的平方  會等於其他兩邊的平方和。由幾何方面來說，如果我們在三邊上各作一個正方形，那麼兩個小正方形的面積和就會等於大正方形的面積


    二.三角形三內角之和等於 180°，如果以弳(radian) 為單位，也可以說三角形三內角之和等於 π  
    內角A 
    內角C 
    內角B


      這本書在當時受到重視，不單只是為了學幾何，主要還要學一種邏輯推理的方法。歐幾里得用幾個很明顯的事實──公理，把幾何的結論從公理用邏輯的方法推出。而在他所列出的公理當中，較受爭議的是平行公理。平行公理原來是說：有兩條直線被一直線所截，如果截角的和小於180°，那麼這兩條直線在充分延長後，必相交於一點。


      一個簡單的說法是：假使有一直線和線外一點，那麼通過那個點就剛剛好只有一條直線和原來的直線平行。平行者，就是這兩條直線不相交


      這個平行公理在所有公理之中是最不明顯的，所以數學家或是對數學有興趣的人便想從其他的公理去推得平行公理。而這努力延持了兩千年，後來證明這是不可能的，於是有了非歐幾何學的發現，這在人類思想史上是非常特別、有意思的事實。因此我感覺到這是西洋數學和中國數學不同的地方。


     《九章算經》是中國古代最有名的數學書，一共九章，第九章談的是所謂勾股，勾、股就是直角三角形中較短約兩個邊，一個叫做勾，另一個就叫做股，而最長的那個邊便稱為弦。勾股定理也就是剛才所謂的畢氏定理，所以它的發現，中國人也應該有份。但是在中國的幾何中，我無法找到類似三角形三內角和等於 180° 推論，這是中國數學中沒有的結果。


      據普羅克拉斯（Proclus, 410～485）的說法，畢氏學派已經知道，用同樣大小且同一種的正多邊形舖地板時，只能用正三角形、正方形與正六邊形，得到三種圖案。然而，數學史家阿爾曼 (Allman) 卻認為，古埃及人習價用這三種正多邊形來舖地板，並且從長期的生活經驗中，觀察而發現「畢氏定理」與三角形三內角和定理。  
    三角形內角和定理


      古埃及人又從舖地板中，發現三角形三內角和為一平角（即180度）。在圖中，繞一頂點的六個角，合起來一共是一周角（即360度），因此正三角形三內角和為一平角。這雖只是特例，但卻是進一步發現真理的契機。


      繞一頂點的四個直角，合起來一共是一周角，因此正方形四角和為一周角」。作正方形的對角線，得到兩個相同的等腰直角三角形，從而得知等腰直角三角形三內角和為一平角。將正方形改為長方形，前述論證也成立，因此任何三角形都可以分割成兩個直角三角形（作一邊的高），所以任意三角形三內角和為一平角。 


    • 將三角形的三個角剪開來（左圖），再將三個角排在一起，就得到一個平角（右圖），著名的偉大科學家巴斯卡（Pascal, 1623～1662）小時候就是如此這般重新發現這個定理。 


    • 我們也可以利用摺紙的實驗，發現這個定理。即沿著  DE、DG、EF 把三角形摺成長方形 DEFG，那麼      疊合於 A' 點，成為一平角。


    利用旋轉鉛筆的實驗，也可看出這個定理 


    畢氏定理 
      這是關於直角三角形三邊規律的定理：對於「任意」的直角三角形都有  c2 = a2 + b2


    • 古埃及人仍然是從舖地板中看出其端倪。在圖中，直角三角形  ABC 斜邊 AB 上的正方形面積，等於兩股上正方形面積之和。這是畢氏定理的一個特例。


    • 我們可以利用幾何板 (geoboard)，玩出更多畢氏定理的特例。以下兩圖就是個例子。 


    • 另一方面，巴比倫人與中國人都觀察到一個木匠法則。即木匠在決定垂直、直角及邊長時，發現邊長為 3, 4, 5 的三角形，三邊具有 32 + 42 = 52 的關係並且為直角三角形（畢氏逆定理之特例）。
    • 這些線索好像是礦苗，人們很快就發現了畢氏定理之「金礦」。這只需用剪刀勞作（夠直觀經驗吧！）就可以看出來。圖中，以邊長 a+b 作兩個正方形；左圖剪掉四個直角三角形，剩下兩個小正方形，面積之和為 a2 + b2；右圖從四個角剪掉四個直角三角形，剩下一個小正方形之面積為 c2；等量減去等量，其差相等。因此 a2 + b2 = c2。
    Posted by at

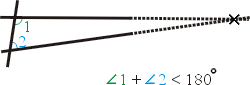
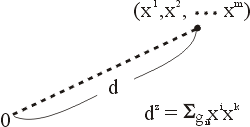
    No comments:

    Post a Comment

    Subscribe to: Post Comments (Atom)