作用量S(x(t))並不是一般的函數,因為一個點x無法經由S(x(t))對應到一實數,而必須有一整條路徑才可成立這對應關係,x(t)→S(x(t))。不過我們仍然可以把S(x(t))看成一個廣義的函數(泛函),而用類
also riemann
在定义函数的社会是要求速降的
http://tieba.baidu.com/p/3035565633
下面我们来个插叙,就是逐步铺开这些吓人的黑话。首先我们讲distribution,函数我们都知道,是在空间每点指定一个复数,而现在我们说distribution是干一件相反的事情,他把一个函数给对应到一个复数,此话怎么讲?用黑话说,这叫做函数空间的对偶空间。用白话就是我们可以举些例子。比如我们把这个函数进行全空间积分就得到一个数,那么这里我们就要指出了,我们用来定义的函数必须具备速降的条件才能得到收敛的积分,这个定义比较繁琐我们就不写出来,但是我们要在心里知道。我们拿出任意一个函数g(x)我们做∫g(x)f(x)dx 也给出一个数,所以我们的distribution可以用一个函数来刻画,在前面直接积分的例子中就是常数1而已,实际上我们在这对g(x)毫无要求,因为我们在定义函数的社会是要求速降的。还有些奇葩的distribution不能用一个函数直接积分上去表示的是熟悉的狄拉克δ,这个东西经常无耻的把自己混到函数里面去其实自己又不能良好定义,而总是只敢以积分的形式出现。
比如δ(f)=f(0)=∫δ(x)f(x)dx。
既然分布是和函数秘密相关我们可以把函数的好东西移植过来,比如对distributionT求导。我们如下定义
打了800多个字 被系统无情删帖,现在从新再来,原来那些润色的文字看来是暂时没空去回复了,简单点写吧,有空再调整。
先说量子力学的定义,力学系统是一个相空间M,其具备一个辛结构,用来体现它的哈密顿运动方程,M上的各种函数是所谓可观测物理量,他们之间可以建立所谓泊松括号运算。所谓量子化是对这个相空间找到一个希尔伯特空间H,使得各种函数变成这里的各种算子,并且泊松括号的结果变成这里的算子对易子。另外所谓力学体系有个对称性是指有个群同态G-->Aut(M),该群同态,对应到希尔伯特空间的一个酉表示G--->U(H)。
所谓公理化,是把一组对象的某些共性抽出来作为这组对象的定义,一般做法是我们抓一堆原料,暴力地要求原料必须满足xxx xxx xxx等法律要求,然后就断定这组原料就是我们需要的那个东西。在此原料本身是怎么抓来的已经被遗忘了,我们是抽出性质作为定义。这种用法在现代数学中是比比皆是,比如根系的公理化定义可以脱离李代数,奇异同调的定义可以脱离拓扑剖分。就像我们最开始通过数苹果认识12345,后来我们发现12345不仅可以用于苹果梨子,也可以用于今天上了几节数学课这样的抽象概念,最后我们用数字是忘掉了苹果的。
下面就先把wightman的公理搬出来,里面的黑话是吓人的,我会逐一用通俗的话解释。
原料1 态矢量空间 为一个希尔伯特空间的射影,也就是两个矢量差一个复数被认同为一样,温伯格大牛在他的量子力学中说,态就是希尔伯特空间的一个射线就是这个意思。
原料2 真空态,是某个或某些矢量。 之所以要说某些是考虑到简并的真空所具有的对称性,真空并不唯一的情况。
原料3 一个酉表示 是庞加莱群P—>U(H)的一个表示,说明我们的量子体系是有传承时空对称性的。
原料4 这个黑话最多,最唬人。 有一组叫做场算符的东东,他的作用是把一个 空间中的函数射到一个算子上。这个定义貌似很难懂,不过换个角度看,也就是先拿一个函数,然后我们用函数和场算符合体,就得到一个算符了。所以场算符叫做算符的分布。分布是个黑话,不过下面我们就要把它变成白话。 睡觉
下面我们来个插叙,就是逐步铺开这些吓人的黑话。首先我们讲distribution,函数我们都知道,是在空间每点指定一个复数,而现在我们说distribution是干一件相反的事情,他把一个函数给对应到一个复数,此话怎么讲?用黑话说,这叫做函数空间的对偶空间。用白话就是我们可以举些例子。比如我们把这个函数进行全空间积分就得到一个数,那么这里我们就要指出了,我们用来定义的函数必须具备速降的条件才能得到收敛的积分,这个定义比较繁琐我们就不写出来,但是我们要在心里知道。我们拿出任意一个函数g(x)我们做∫g(x)f(x)dx 也给出一个数,所以我们的distribution可以用一个函数来刻画,在前面直接积分的例子中就是常数1而已,实际上我们在这对g(x)毫无要求,因为我们在定义函数的社会是要求速降的。还有些奇葩的distribution不能用一个函数直接积分上去表示的是熟悉的狄拉克δ,这个东西经常无耻的把自己混到函数里面去其实自己又不能良好定义,而总是只敢以积分的形式出现。
比如δ(f)=f(0)=∫δ(x)f(x)dx。
既然分布是和函数秘密相关我们可以把函数的好东西移植过来,比如对distributionT求导。我们如下定义:
partial i T(f)=-T(partial i f) 也就是说定义distribution的导数为,它作用与函数等于原来的分布作用在函数的导数。
假定如上用函数g定义的distribution记作Tg 读者可以证明 偏Tg,的结果正好等于T偏g。所以我们上面插一个负号的定义方式看似不自洽,其实刚好自洽。
比如δ(f)=f(0)=∫δ(x)f(x)dx。
既然分布是和函数秘密相关我们可以把函数的好东西移植过来,比如对distributionT求导。我们如下定义:
partial i T(f)=-T(partial i f) 也就是说定义distribution的导数为,它作用与函数等于原来的分布作用在函数的导数。
假定如上用函数g定义的distribution记作Tg 读者可以证明 偏Tg,的结果正好等于T偏g。所以我们上面插一个负号的定义方式看似不自洽,其实刚好自洽。
下面我们看到用这种求导运算可以给出狄拉克的δ。我们用在0到无穷取1的Heaviside阶跃函数做distributionTH(f)=∫0到∞ f(x)dx 现在做TH的导数:
求导T(f)=-∫ 求导f(x)dx=f(0) 所以我们高兴地发现δ其实是H的导数而已。也就是说δ这种奇葩的distribution也可以用某个正常的函数给出的distribution求导给出!
这就是结论任意一个distribution总能用那种函数积分给出的distribution做各种导数的有限组合给出。我们说了关于distribution的导数,终究目的只是为了建立关于distribution的微分方程运算埋下伏笔。其实这就是我们要建立的klein Gordon方程。
求导T(f)=-∫ 求导f(x)dx=f(0) 所以我们高兴地发现δ其实是H的导数而已。也就是说δ这种奇葩的distribution也可以用某个正常的函数给出的distribution求导给出!
这就是结论任意一个distribution总能用那种函数积分给出的distribution做各种导数的有限组合给出。我们说了关于distribution的导数,终究目的只是为了建立关于distribution的微分方程运算埋下伏笔。其实这就是我们要建立的klein Gordon方程。
下面介绍完PDE就睡觉。PDE的坐标是一堆偏导算子的多项式,作用在一个函数=另一个函数的形式。下面我们要对distribution干这件事。我们用α代表 一簇(a1 a2。。。。an)
这是为了体现在多维流形上做运算的方便。我们用partial^α代表对各个自由度进行(a1 a2。。。。an)的偏导。在配上一个系数c(a1 a2。。。。an)成为∑cα(-i*partial)^α。记作P(-i*partial)
P代表整数环上的多项式 一个PDE表述为P(-i*partial)u=v 其中u v都是distribution!
那么我我们把格林函数那套玩意搬过来 定义P(-i*partial)G=δ!于是用这个格林函数就能产生要的解,其手段就是卷积!
这是为了体现在多维流形上做运算的方便。我们用partial^α代表对各个自由度进行(a1 a2。。。。an)的偏导。在配上一个系数c(a1 a2。。。。an)成为∑cα(-i*partial)^α。记作P(-i*partial)
P代表整数环上的多项式 一个PDE表述为P(-i*partial)u=v 其中u v都是distribution!
那么我我们把格林函数那套玩意搬过来 定义P(-i*partial)G=δ!于是用这个格林函数就能产生要的解,其手段就是卷积!
承接格林函数讲最后一点, 利用卷积的定义
u*x=∫u(y)v(x-y)dy ,可以定义一个distribution和函数的卷积,它还是一个distribution
对T 定义T*g(f)=T(g*f),结论给出u=G*v将给出P(-i*partial)u=v 的解。
以上我们对distribution有了感性认识。
下面讲傅立叶分析 我们记u的傅立叶变换是U,U=∫_R^n u(x)e^ipx 对于一个R^n p的一般形式为(p1 p2....pn)。
傅立叶变换是函数 --->函数,因此我们可以诱导定义傅立叶变换distribution--->distribution。
只需定义distribution--->distribution复合上傅立叶变换。
如下:F(T)(f)=T(F(f)) 其中f为速降函数。
既然这样定义,同学还可以验证一个事情,对于由函数g给出的distribution Tg,对Tg做傅立叶变换将等价于对g做傅立叶变换,说明我们的定义是自洽的。
u*x=∫u(y)v(x-y)dy ,可以定义一个distribution和函数的卷积,它还是一个distribution
对T 定义T*g(f)=T(g*f),结论给出u=G*v将给出P(-i*partial)u=v 的解。
以上我们对distribution有了感性认识。
下面讲傅立叶分析 我们记u的傅立叶变换是U,U=∫_R^n u(x)e^ipx 对于一个R^n p的一般形式为(p1 p2....pn)。
傅立叶变换是函数 --->函数,因此我们可以诱导定义傅立叶变换distribution--->distribution。
只需定义distribution--->distribution复合上傅立叶变换。
如下:F(T)(f)=T(F(f)) 其中f为速降函数。
既然这样定义,同学还可以验证一个事情,对于由函数g给出的distribution Tg,对Tg做傅立叶变换将等价于对g做傅立叶变换,说明我们的定义是自洽的。
傅立叶变换把偏导对应到-ip 原因很简单:
F(偏k f)=∫(偏k f)e^ixp dx 用分部积分=-∫f ip_k e^ipx dx=-ip_k F(f)
所以结论是F(偏^α)=(-ip)^α F
意义在于我们能把微商多项式的PDE变成一般系数的方程。
现在就剩下多项式乘以distribution得到另个一distribution的过程了。换句话说我们在做distribution对多项式的除法。记方程PT=1的解为F(G) P代表多项式 F代表傅立叶变换,那么结果就是G就是方程P(-i偏)G=δ的解,也就是我们所谓的格林函数。
验证上面的结论 只需要渎者对1这个分布做傅立叶 得到δ。
F(偏k f)=∫(偏k f)e^ixp dx 用分部积分=-∫f ip_k e^ipx dx=-ip_k F(f)
所以结论是F(偏^α)=(-ip)^α F
意义在于我们能把微商多项式的PDE变成一般系数的方程。
现在就剩下多项式乘以distribution得到另个一distribution的过程了。换句话说我们在做distribution对多项式的除法。记方程PT=1的解为F(G) P代表多项式 F代表傅立叶变换,那么结果就是G就是方程P(-i偏)G=δ的解,也就是我们所谓的格林函数。
验证上面的结论 只需要渎者对1这个分布做傅立叶 得到δ。
Klein Gordon方程 我们重点认识KG方程格林函数与由之给出的一般解。一个普通KG方程的形式为 (口+M^2)u=v 我们直接在FT空间来求格林函数(-p^2+m^2)T=1
T=(m^2-p^2)^-1 虽然写成了函数形式但心里要知道,T本质上是由(m^2-p^2)^-1形式给出的distribution!所谓传播子就是(m^2-p^2)^-1的傅立叶变换 回去坐标空间结果:
G=(2π)^-4 ∫(m^2-p^2)^-1 exp(-ipx)dp。
没错这就是动量空间和坐标空间的传播子!他们是distribution!
T=(m^2-p^2)^-1 虽然写成了函数形式但心里要知道,T本质上是由(m^2-p^2)^-1形式给出的distribution!所谓传播子就是(m^2-p^2)^-1的傅立叶变换 回去坐标空间结果:
G=(2π)^-4 ∫(m^2-p^2)^-1 exp(-ipx)dp。
没错这就是动量空间和坐标空间的传播子!他们是distribution!
回到四维时空量子场论中来我们学过的是自由的KG方程 是所谓物理波函数的方程:
(口+M^2)φ=0 切换到傅里叶 (-p^2+m^2)F(φ)=0 也就是F(φ)不为0的话 一定要满足
p^2=m^2,用黑话叫做F(φ)的支撑集p^2=m^2的超曲面。 伟大的哲学物理学家的话说就是物理的本质彻底裸露了,KG方程无非就是相对论性的质壳条件!既然支撑集在这样一个紧致的0测度超曲面上,我们可以认为它正比于δ(p^2-m^2) 比例系数设为g(p)。傅立叶变换回去就是说波函数形式如下 (2π)^-4 ∫g(p)δ(p^2-m^2) exp(-ipx)dp。用李三清的话来说就是KG的解是一系列在平面波的叠加,动量仅仅在在壳条件上超曲面上取值! 今天到此为止!希望对大家能有所帮助
(口+M^2)φ=0 切换到傅里叶 (-p^2+m^2)F(φ)=0 也就是F(φ)不为0的话 一定要满足
p^2=m^2,用黑话叫做F(φ)的支撑集p^2=m^2的超曲面。 伟大的哲学物理学家的话说就是物理的本质彻底裸露了,KG方程无非就是相对论性的质壳条件!既然支撑集在这样一个紧致的0测度超曲面上,我们可以认为它正比于δ(p^2-m^2) 比例系数设为g(p)。傅立叶变换回去就是说波函数形式如下 (2π)^-4 ∫g(p)δ(p^2-m^2) exp(-ipx)dp。用李三清的话来说就是KG的解是一系列在平面波的叠加,动量仅仅在在壳条件上超曲面上取值! 今天到此为止!希望对大家能有所帮助
讲了这么多distribution,我们现在就是告诉大家为啥我们需要的是distribution而不是流形上的算子呢。 那是因为我们量子化的等时对易关系会蹦出来一个δ 这在算子意义下不能良好定义的,所以我们需要的是一个算子的distribution,就如同我们在量子力学没有厚脸皮把δ称为函数一样!
讲了很多 似乎脱离了物理,所以我决定悬崖勒马,先丢一个式子出来。让物理学子 看了有印象
Φ(t,x)=(2π)^-D∫ R^D-1 [a(p)e^ipx-w(p)t+a*(p)e^-ipx+iw(p)t] 这是大家熟悉的场算符!fock展开!我们那个所谓的物理书上的量子场论 就是暴力地说 Φ是个算符,这叫二次量子化!然后a(p) a*(p)也是算符叫什么升降算符,然后大用特用,最后在正则量子化下用各种 升降算符夹在真空态之间 互相打架最后给出所谓的费曼图。但是数学学子看到就会迷糊,到底是个神马玩意叫做场算符,他在哪里呢,能不能让我看得见摸得着,不然那我们怎么理解他。
Φ(t,x)=(2π)^-D∫ R^D-1 [a(p)e^ipx-w(p)t+a*(p)e^-ipx+iw(p)t] 这是大家熟悉的场算符!fock展开!我们那个所谓的物理书上的量子场论 就是暴力地说 Φ是个算符,这叫二次量子化!然后a(p) a*(p)也是算符叫什么升降算符,然后大用特用,最后在正则量子化下用各种 升降算符夹在真空态之间 互相打架最后给出所谓的费曼图。但是数学学子看到就会迷糊,到底是个神马玩意叫做场算符,他在哪里呢,能不能让我看得见摸得着,不然那我们怎么理解他。
下面再看下几何P^=M^2是个啥玩意呢?P既然是时空流形的对偶空间,我们不妨直接看作等价,时空流形 在KK理论 SUGRA理论里面是11维的,在一般玩量子场论里面是4维的,虽然我们不知道真的是多少维度,我们总可以假定是D维,其中一维是时间,我们说P^2就是 那个(+-------)的度规了如果空间度规是1,那么就是我们知道的双曲线了。现在我们把空间度规变成2,也就是推广了一个SO(2)的对称性,吧双曲线做SO(2)旋转就是我们的旋转双曲面!依次类推,空间变成SO(n-1)也一样!我们把双曲线hold住时间轴不动,继续用SO(n-1)去转之就是一个旋转双曲面!顺说下为什么我们要强调是SO群不是O群呢,因为在场论水平的物理是破坏宇称而且有手征现象的。
方便的是由于P^=M^2是我们物理态存在的超曲面,我们可以把它看成是一个约束,它是坐标空间的运动规律到对偶空间--FT空间的对应,通俗的说运动规律给了我们在坐标空间的运动方式,实际上等价于说他在动量空间是在P^=M^2这个超曲面上跑动。逻辑也合情合理,一个运动方程扼杀了一个自由度,所以变成了低一维的嵌入子流形了!
既然那个P^=M^2是 n-1的嵌入子流形,那我们岂不是可以只用n-1个坐标就描述了。其实技巧很简单,那就是来两套坐标卡。两套坐标卡的原因其实不难,从方程的角度看是因为平方导致的双值!从流形的角度看是拓扑的不平庸。我们设计上平面的坐标卡是将空间动量P(n-1维,你可以当三动量来看),射到四动量里面去。也就是P--->(+w(P) P) P--->(-w(P) P) 。这样我们就把。这样我们就对超曲面给了坐标卡,如果我们要对超曲面赋予一个不变测度。我提示两个做法!首先我们可以在超曲面诱导出超曲面上的度量,另外就是直接在D维几分钟插入δ(P^2-M^2)积掉p0。。。
其中dS是超曲面上的不变测度。
再回头看Φ(t,x)=(2π)^-D∫ R^D-1 [a(p)e^ipx-w(p)t+a*(p)e^-ipx+iw(p)t]dS
我们声明a(p)是在n-1的空间里面取的动量,读者可以轻松验证(口+M^2)Φ=0
也就是我们给出了KG方程的解的形式!此时a(p) a*(p)还是 函数 取值在空间动量里面的。接下来我们就要把它变成算子!所以还是简单介绍一下算子的概念。
一个稠密子集上定义的算子A,我们指出有个伴算子,由于在H上定义有内积,伴算子就定义为
<A*f,g>=<f,Ag> A=A* 这里我们回避了 闭算子 闭图像定理等定义, 我们引入一个概念就是算子的domain,就是所谓的定义域。既然<A*f,g>=<f,Ag>,可以考察一下A*的domain,也就是存在一个h使得A*f=h 对任意的g成立!这就是A*的domain。闭算子是用闭图像来定义的,所谓图像是HxH的子集,由(f,Of)组成!如果图像是闭的,称算子是闭的。闭的意义在于序列的极限不会跑出集合之外
再回头看Φ(t,x)=(2π)^-D∫ R^D-1 [a(p)e^ipx-w(p)t+a*(p)e^-ipx+iw(p)t]dS
我们声明a(p)是在n-1的空间里面取的动量,读者可以轻松验证(口+M^2)Φ=0
也就是我们给出了KG方程的解的形式!此时a(p) a*(p)还是 函数 取值在空间动量里面的。接下来我们就要把它变成算子!所以还是简单介绍一下算子的概念。
一个稠密子集上定义的算子A,我们指出有个伴算子,由于在H上定义有内积,伴算子就定义为
<A*f,g>=<f,Ag> A=A* 这里我们回避了 闭算子 闭图像定理等定义, 我们引入一个概念就是算子的domain,就是所谓的定义域。既然<A*f,g>=<f,Ag>,可以考察一下A*的domain,也就是存在一个h使得A*f=h 对任意的g成立!这就是A*的domain。闭算子是用闭图像来定义的,所谓图像是HxH的子集,由(f,Of)组成!如果图像是闭的,称算子是闭的。闭的意义在于序列的极限不会跑出集合之外
泛函分析是线性代数往Hilbert空间的推广,算子的谱 是推广的矩阵本征值问题! 定义为
自伴算子A的谱 是 使得(A-aI)这个算子的逆不是有界算子的那些a,a属于复数域C。I是恒等算子 等价于单位矩阵。当A是自伴随它的谱属于实数R。这个是不是和物理上厄米算符的本征值实数很像?
下面的结论很像李群。我们指出存在一个单参子群,或者说是R的一个酉表示!R---->U(H),满足U(t)的切矢为自伴算子 A,也就是说 lim t--->0 [U(t)-f]/t=--iAf! 我们也可以写成
U(t)=EXP(-itA)学过群论的同学可以想一下,一个酉群U(N)它的李代数是什么形式的。
自伴算子A的谱 是 使得(A-aI)这个算子的逆不是有界算子的那些a,a属于复数域C。I是恒等算子 等价于单位矩阵。当A是自伴随它的谱属于实数R。这个是不是和物理上厄米算符的本征值实数很像?
下面的结论很像李群。我们指出存在一个单参子群,或者说是R的一个酉表示!R---->U(H),满足U(t)的切矢为自伴算子 A,也就是说 lim t--->0 [U(t)-f]/t=--iAf! 我们也可以写成
U(t)=EXP(-itA)学过群论的同学可以想一下,一个酉群U(N)它的李代数是什么形式的。
上面的结论叫做Stone定理,实际上其逆也是成立的!
下面开始定义我们“熟悉的”场算符是一个算子值的distribution
Φ f----->O 其中O是一个算子!f是定义在时空流形上的函数。
其实这种思路很自然,一开始我们想定义函数,就是在时空的没一点赋予一个复数,但是行不通,所以我们转而定义distribution f---->C ,现在我们想在时空没一点赋予一个场算符,这也行不通,所以我们转而定义distribution f---->O。
下面开始定义我们“熟悉的”场算符是一个算子值的distribution
Φ f----->O 其中O是一个算子!f是定义在时空流形上的函数。
其实这种思路很自然,一开始我们想定义函数,就是在时空的没一点赋予一个复数,但是行不通,所以我们转而定义distribution f---->C ,现在我们想在时空没一点赋予一个场算符,这也行不通,所以我们转而定义distribution f---->O。
明天又是周1要上班,所以我们用一些物理来结束以上的场算符!模型是locally定义的,实际上没有测量是完全定域的,这是测不准原理的要求,这就导致了我们的量子场论必须经历重整化!所谓测量不是定域的,也就是我们只能在一定范围内测出我们需要的物理量--也就是一个期望值,其实这个过程对应于我们用场算符和这个支撑集范围内的一个函数的作用给出的算子的期望值!
下面是对称性的注入!相对论的要求其实是ponicare对称性,ponicare群是 平移和lorentz的半直积,ponicare变换保持时空的因果结构,并保持时空两点的类空性。ponicare群记作
(a,L) 前者是平移 后者是洛伦兹转动。定义它在流形上的函数的作用采用自然的方式,直接把ponicare群的逆作用到宗量里去!也就是Af(x)=f(A^-1 x)。如果是张量函数,或者旋量函数我们还要在前面乘上群的表示。同样有张量函数的话,我们也可以推广到算子值张量分布,它的意思是说 给定一个函数,再给定一些矢量 对偶矢量 ,用算子值张量分布作用之才能得到一个算子!在这里我是用多重线性代数的角度说张量的,同学们可以用服从洛伦兹群的直积表示的分量来认识张量。
高涌泉 作用量S(x(t))並不是一般的函數,因為一個點x無法經由S(x(t))對應到一實數,而必須有一整條路徑才可成立這對應關係,x(t)→S(x(t))。不過我們仍然可以把S(x(t))看成一個廣義的函數(泛函),而用類似微積分中求極值的辦法去求【瀏覽原件】,並證明【瀏覽原件】是牛頓方程式的解
(a,L) 前者是平移 后者是洛伦兹转动。定义它在流形上的函数的作用采用自然的方式,直接把ponicare群的逆作用到宗量里去!也就是Af(x)=f(A^-1 x)。如果是张量函数,或者旋量函数我们还要在前面乘上群的表示。同样有张量函数的话,我们也可以推广到算子值张量分布,它的意思是说 给定一个函数,再给定一些矢量 对偶矢量 ,用算子值张量分布作用之才能得到一个算子!在这里我是用多重线性代数的角度说张量的,同学们可以用服从洛伦兹群的直积表示的分量来认识张量。
高涌泉 作用量S(x(t))並不是一般的函數,因為一個點x無法經由S(x(t))對應到一實數,而必須有一整條路徑才可成立這對應關係,x(t)→S(x(t))。不過我們仍然可以把S(x(t))看成一個廣義的函數(泛函),而用類似微積分中求極值的辦法去求【瀏覽原件】,並證明【瀏覽原件】是牛頓方程式的解
作用量S(x(t))並不是一般的函數,因為一個點x無法經由S(x(t))對應到一實數,而必須有一整條路徑才可成立這對應關係,x(t)→S(x(t))。不過我們仍然可以把S(x(t))看成一個廣義的函數(泛函),而用類似微積分中求極值的辦法去求【瀏覽原件】,並證明【瀏覽原件】是牛頓方程式的解
從歐幾里得到微分幾何
什麼是幾何學 (第 5 頁) 陳省身 整理:林麗明 |
.原載於科學月刊第十八卷第六期 ‧對外搜尋關鍵字 |
|
#發行日期:1995、03
#期號:0303
|
量子力學、費曼與路徑積分
毫無疑問的,二十世紀物理學中最重要的二個成就是相對論(Relativity)與量子力學(Quantum mechanics)。然而這兩門學問誕生的方式與展現的風格,卻大不相同。相對論(狹義與廣義)出現時,就已經像一顆雕琢精緻、光芒耀眼的鑽石,是一完美無缺的藝術品。其創造者愛因斯坦(A.Einstein, 1879~1955)從一個非常基本的物理原則,即「對稱原理」出發,推演出一套幾乎無懈可擊的數學架構,所以相對論有一種非得如此不可的氣勢。難怪愛因斯坦曾很有信心地對朋友說:「沒有人在理解它之後,能逃離這理論的魔力」。
雖然相對論在一般人的印象裡是一個非常玄妙深奧的理論,其實比較起來,描述微觀世界規則的量子力學是更為怪異,幾近於荒誕的學說。相對論可以說是愛因斯坦一人的心血結晶,而量子力學卻是集眾人之力,一點一滴累積起來的。不過在建立量子力學過程中,還是有一些關鍵時刻,特別是在1925年海森堡(W.Heisenberg, 1901~1976)發現:任何一個物理量都可以由一矩陣來代表。海森堡找到了這些矩陣所應遵循的方程式。海森堡的成功來自於他對實際物理現象的深刻了解,以及誰也無法解釋的靈感。
在海森堡提出他的矩陣力學半年之後,薛丁格(E.Schrodinger, 1887~1961)發表了另一個方程式,也可以正確地計算出與實驗結果相符的物理量。薛丁格的出發點是將物質(例如電子)看成是波動。這和海森堡依舊把電子當成粒子是截然不同的。不過人們很快地就理解到海森堡與薛丁格二人的理論在數學上是等價的(equivalent),所以我們終究只有一套而非兩套量子力學。
先前筆者已提過,相對論是從一個非常自然的物理原則出發,繼而推導出數學方程式。而在量子力學的情形則是在尚未能看清全局時,我們就已找到了適用的方程式。許多物理學者,包括一些對量子力學有很大貢獻的人,曾以為人們很快就會發現量子力學出錯的地方。沒想到我們至今仍未碰到量子力學有任何不妥之處。這是非常驚人的;總之,儘管今天物理學者還在爭辯量子力學方程式的物理意義為何,這些方程式的正確倒是無庸置疑的。
在本篇文章中,筆者想介紹量子力學最有趣的一種數學表現方式,即理查‧費曼(Richard Feynman,1918~1988,依發音應翻譯成理查‧范恩曼)所發明的路徑積分(Path Integral)。這理論發表於1948年《現代物理評論》(Review of Modern Physics)期刊上。費曼其實更早在1941年就已完成這一工作;當年他才23歲,還是研究生。只因為二次大戰期間費曼投入曼哈坦(Manhattan)原子彈製造計畫,所以延遲發表這一項在很多人的評價裡是費曼最重要的作品。
費曼是二十世紀後半期風頭最健的物理學家,他在台灣也頗為一般人所知。原因是有關於他傳奇事蹟的中文書籍有不少讀者。凡是讀過《別鬧了費曼》(Surely you are joking, Feynman)、《你管別人怎麼想》(What do you care what other people think)或《天才的軌跡》(Genius)的讀者,很難不著迷於費曼那熱情的性格,獨特的人生觀及不凡的遭遇。
話說回來,讓費曼在物理界成名的,倒不是路徑積分而是他在量子電動力學上的貢獻。特別是他所發明的費曼圖,已成為理論物理學者不可缺少的研究工具。圖一是費曼圖的一個例子。這個圖代表電子與電子的碰撞。
其中實線代表電子,波浪線代表光子(交互作用)。每個費曼圖除了給所要描述的物理現象一個非常直覺、清楚的圖像外,還可以幫助我們輕易而精確地分析這些現象。原因是費曼有一套人們稱為費曼法則(Feynman Rule)的步驟,可以將費曼圖對應到特定的數學式子。透過這個數學式子的計算,我們就能定量地掌握費曼圖所代表的物理現象。一般而言,較複雜的費曼圖(見圖二)所對應的數學式子,處理起來也比較困難,這往往要借助計算機才能得到結果。
二次大戰結束後,物理學家從武器研發工作回到學術崗位。那時量子電動力學是研究焦點。在眾多逐鹿者之中,徐文格(J.Schwinger)與朝永振一郎(Sin Ichiro Tomonaga)最早得到突破,他們率先從複雜的計算中取得與精密實驗一致的結果。費曼則以他的費曼圖異軍突起,甚至有後來居上的聲勢。朝永、徐文格與費曼三人的工作為二十世紀後半眾多理論物理進展打下基礎,稱得上具承先啟後的樞紐地位。為此他們三人共同獲得1965年諾貝爾獎。三人中較年輕的費曼、徐文格二人皆出生於1918年,也都因癌症於近年去逝。二人都在年輕時已顯露其數理天才,也都是很早就被認定會在科學上有了不起的貢獻。二人之間有一種很微妙的,既是科學道路上的伙伴也是競爭者的關係。1945年,在美國發展原子彈的洛斯阿拉摩斯(Los Alamos)實驗室,費曼與徐文格第一次見面。那時兩人只有27歲,而徐文格已發表有二、三十篇文章,算是小有名氣。費曼對徐文格說:「我什麼都還沒作出來時,你卻已在一些事情上留下名字了。」費曼那時不知道,假如他們二人自第一次見面起就不再有新作品,從後代眼光看,費曼憑他的路徑積分就足以和徐文格分庭抗禮、平起平坐,甚或還略勝一籌的。
回到本文主題,以下筆者就要介紹路徑積分。這得從古典力學講起。古典力學的核心是牛頓運動方程式,這方程式可以描述物體(如粒子)的運動軌跡。它的形式是大家都很熟悉的
F=ma (l)
其中F代表物體所受的力,m是物體質量,a是加速度;也就是物體所在位置對時間的二次微分。一旦知道物體在某一時刻ti的位置xi及其速度vi,我們就可以經由解牛頓方程式(l),得到物體在ti以後時刻的軌跡(見圖三)。
自十七世紀牛頓發表他的名著《自然哲學的數學原理》闡明其力學原理以來,人們仍不斷地在充實古典力學的數學架構。除了靠解微分方程式以求得運動軌跡之外,另外還有一個從表面上看很不相同,但其實在數學上是等價的方法,也就是從積分觀點著手的「最小作用量原理」(least action principle)。這個原理的敘述是這樣的:
若我們要知道當物體從(ti,xi)時空點走到(tf,xf)時空點,到底是循著那一條路徑x(t)時[見圖四,在無窮多可能的路徑中,筆者只代表性地劃了三條路徑x1(t),x2(t),x3(t)〕,我們只要計算一個積分:
【瀏覽原件】 (2)
在積分式子中,v(t)是物體在t時刻的速度,【瀏覽原件】,所以【瀏覽原件】也就是動能,v(x(t))是物體在x(t)位置的位能。把任何一條路徑x(t)代入蕞n分式(2),都有一個相對應的值S(x(t)),S被稱為作用量(action)。物體真正走的路徑只有一條,讓我們把它記作【瀏覽原件】。【瀏覽原件】的特點就是:它所對應的作用量【瀏覽原件】比其他所有不對的路徑所對應的S值都還要小。亦即【瀏覽原件】是S(x(t))函數的極小值(見圖五)。我們可以從數學上證明對應到最小作用量的路徑【瀏覽原件】,也滿足牛頓運動方程式。在微積分中,我們若要求某一個函數f(x)的極大或極小值,我們只要算f(x)的微分【瀏覽原件】,而後找【瀏覽原件】的解就可得到答案。前面提到的作用量S(x(t))並不是一般的函數,因為一個點x無法經由S(x(t))對應到一實數,而必須有一整條路徑才可成立這對應關係,x(t)→S(x(t))。不過我們仍然可以把S(x(t))看成一個廣義的函數(泛函),而用類似微積分中求極值的辦法去求【瀏覽原件】,並證明【瀏覽原件】是牛頓方程式的解(對細節有興趣的讀者,可參閱任何一本理論力學教科書或是費曼非常有名的物理學演講《Feynman Lectures on Physics》中的第二冊十九章。)
從最小作用量原理的觀點來理解古典力學,我們得到的是一個與微分觀點截然不同的意象。我們並不是一小段一小段逐步地推算出物體的軌跡,而是將所有可能路徑拿來比較,找出給我們最小作用量的路徑。在某一些問題中,最小作用量原理其實比微分方程式更方便。
古典力學的架構雖完備,卻不能適用於原子尺度大小的微觀世界。在那裡我們得改用量子力學的法則,而這些法則是我們完全無法從在古典力學裡所獲得的經驗去理解的。在古典物理中,我們可以同時測量在某一時刻物體的位置與速度(動量),所以可以得知往後物體運動的情形。但在量子世界裡,我們不能同時測知物體的位置與速度,所以無法完全掌握物體動向(即測不準原理)。也就是說,我們得放棄「物體運動是循著某一特定路徑」這一概念。
若經由測量,我們得知某物體(例如電子)在ti時刻位於xi位置,我們並不能確知在tf時刻(tf>ti),物體會在那裡。量子力學能夠告訴我們的是:如何計算物體在tf時刻可能位於xf的機率有多少。我們將這機率記作P(tixi→tfxf)。要知道P,得先計算一個叫作機率振幅(probability amplitude)的複數〈tf,xf ︳ti,xi〉(這記號是量子力學創造者之一狄拉克(Dirac)發明的)而機率P就等於
P(tixi→tfxf)= ︳〈tf,xf ︳ti,xi〉︳2 (3)
因為機率振幅(由它可推導出許多讀者可能知道的「波函數」)本身是複數,不可能是一個可測量的物理量,所以它的物理意義一直為人爭論不休。在此筆者不談這一棘手的問題,我們要學的是費曼計算機率振幅的辦法。費曼給了以下一個算式:
【瀏覽原件】(4)
方程式右邊的S(x(t))是路徑x(t)的作用量,【瀏覽原件】,是普郎克常數除以2π(嚴格講,必須在(4)式右邊乘上一個常數A,A可由機率守恆的條件來決定)。也就是說,要得到機率振幅,我們需要計算所有從(ti,xi)時空點到(tf,xf)時空點可能的路徑(例如x1(t),x2(t),x3(t),見圖四)所對應的作用量,然後計算eis(x(t)),並將它們加起來。因此在量子力學中除了對應到最小作用量的古典路徑之外,其他在古典世界中不會出現的路徑,也有不可忽視的作用。
我們也可以把(4)式寫成積分的形式:
【瀏覽原件】 (5)
不過它的內涵和(4)式是完全一樣的。因為我們要將所有路徑的貢獻積(加)起來,方程式(5)的右邊就被稱為路徑積分。它最大的好處就是給機率振幅一個很圖像式的詮釋角度。讓我們比較可以從幾何的觀點而非純代數操作的角度來理解量子力學。
路徑積分另一個長處是:很容易看出在數學上量子力學是如何和古典力學連接起來。於古典物理中,
目前費曼的路徑積分、海森堡的矩陣力學及薛丁格的波動力學,可說是量子力學理論三個最重要的數學表現形式。這些不同的形式都各有其優點。近年來,路徑積分在量子力學之外,也滲透進統計力學及數學中的幾何、拓撲等領域。數學家發現他們也得懂一點路徑積分才能閱讀最新的數學成果。一些數學家也努力於為路徑積分建立一嚴謹的數學基礎。我們可預見:在未來,路徑積分會是一更廣闊蓬勃的研究領域,這是其發明者在50年前完全沒有想到的。
最後筆者必須說明,費曼發明路徑積分的靈感,來自狄拉克發表於1933年的一篇文章。狄拉克的文章提出一個問題:古典力學中很重要的作用量這個觀念是如何出現在量子力學中的?〔海森堡與薛丁格的理論只運用了古典力學中的漢密爾頓量(Hamiltonian)〕,而狄拉克自己也給了初步的答案。我們可以說路徑積分是兩位天才合力建造出的一個美妙理論。
高涌泉任教於台灣大學物理系,本刊編輯委員
高涌泉
古典力學中的漢密爾頓量(Hamiltonian),一般記作H,基本上就是能量。也就是:
【瀏覽原件】
在本文中,我們介紹了作用量S(x(t))〔見2)式],S(x(t))是函數【瀏覽原件】=動能-位能於路徑x(t)上的積分值。L被稱為拉格蘭其量(Lagrangian)。漢密爾頓(W.R.Hamilton,1805~1865)與拉格蘭其(J.L.Lagrange,1736~1816)皆是於古典力學有重大貢獻的數學家。
在海森堡的矩陣力學中,漢密爾頓量H成為一個矩陣,而海森堡的力學方程式為:
【瀏覽原件】
其中x(t)也是矩陣,代表物體的位置。
H在薛丁格的波動力學中,變成一個數學算符(operator),它可以作用在函數上。薛丁格有名的波動方程是:
【瀏覽原件】
| ||




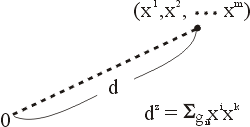
No comments:
Post a Comment