标签:
杂谈 |
反应焓变是包括体积变化做功的,只不过高中课不讲。吉布斯自由能减小只是表明反应发生在热力学上的可能性,表明这个反应不违反热力学定律,并不表示反应能发生,因为它还取决于动力学
大位能是統計力學中使用的一個量,特別是在開放系統的不可逆過程裡使用。
大位能被定義為
大位能的改變量為
當系統達到熱動力平衡,ΦG有最小值。可以由考慮到當定體積且溫度與化學位停止改變時dΦG為零而見到。
對於理想氣體,

這以羅斯物理學家列夫·朗道命名。取決於系統的規定,這可能是大位能的同義詞。
关于自由能的一些讨论
收稿日期 :2003 - 01 - 23 ;修回日期 :2003 - 11 - 03
作者简介 :郭革新(1967 —) ,男 ,河北徐水人 ,河北师范大学物理学院副教授 ,河北工业大学材料物理与化学专业博士生 ,主要从事铁电物理
和磁畴壁物理的研究.
郭革新1 ,2
,周国香1
,王爱坤1 ,3
,何文辰1
(1. 河北工业大学理学院 ,天津 300130 ;2. 河北师范大学物理学院 ,河北石家庄 050016 ;3. 河北科技大学物理系 ,河北石家庄 050018)
摘要 :给出了自由能函数的完整表达式 ,并说明了自由能展开式中各项的物理意义. 指出了自由能展开式系数及自变量
的共轭变量的意义 ,吉布斯自由能的一阶偏导数都是热力学变量 ;吉布斯自由能的二阶偏导数一律都是物性张量. 讨论了相
变过程中的自由能函数展开式应保留的项数等 ,还给出了相稳定性条件.
关键词 :自由能 ;展开式 ;相变 ;Landau 理论
中图分类号 :O 414. 13 文献标识码 :A 文章编号 :100020712 (2004) 0620019204
1 引言
用 Landau 理论研究结构相变时 ,首先要正确写
出所研究体系的吉布斯自由能的表达式. 本文尝试
给出了自由能的完整表达式及自由能展开式中各项
的物理意义. 指出了自由能展开式系数及自变量的
共轭变量的意义 ,这一点在许多文献中都未明确涉
及[1~4 ] ,即 :吉布斯自由能的一阶偏导数都是热力学
变量 ;二阶偏导数一律都是物性张量. 特别是在讨论
相变过程时 ,自由能函数展开式应保留多少项 ,以前
的文献也未作深入讨论[1~4 ] . 本文较详细地讨论了
这些问题. 另外 ,本文还给出了相稳定性条件.
2 吉布斯自由能的表达式及其物理意义
2. 1 热力学函数及变量
热力学变量可分为两类 ,即广延量与强度量. 广
延量如 : P (电极化强度) , M (磁化强度) , S (应变) ,
S 3 (熵) 等 ,它们与体系质量或体系中所含的分子数
成正比 ;强度量如 : E (电场强度) , H (磁场强度) ,
T(应力) ,Θ(热力学温度) 等 ,它们与体系质量无
关. 广延量与强度量的对应关系见表 1[1] . 它们是一
对对相互共轭的 ,对于粒子数可变系统还要考虑μ
表 1 广延量与强度量的对应关系表
强度量(广义力) Xi
广延量(广义坐标) x i
元外功 d W = Xi d x i
电场强度 E
电极化强度 P
电极化功 E・d P
磁场强度 H
磁化强度 M
磁化功 H・d M
应力 T
应变 S
应变功 T・dS
热力学温度 Θ
熵 S 3
吸热 d Q = Θd S 3
(化学势) 和 n (物质的量) . 每个热力学函数的自变
量在每一对共轭的广延量和强度量之间只取一个.
U = U ( S , P , S 3 )
F = F( S , P , S 3 )
H = H( T , E , S 3 )
H1 = H1 ( T , P , S 3 )
H2 = H2 ( S , E , S 3 )
G = G( T , E ,Θ)
G1 = G1 ( T , P ,Θ)
G2 = G2 ( S , E ,Θ)
所有这些热力学函数互相之间通过勒让德变换
相联系. 自由能函数应该是标量(0 阶张量) ,显然它
是热力学变量( T , Tij , Pi , Mi , n) 的函数. 只有各向
同性的态(项) ,它才是( T , P , x) 的函数.
2. 2 内能的表达式及其物理意义
内能的表达式为
ΔU =ΔU ( S , P , M , S 3 ) = W + Q
(1)
其中 , W 表示外界对系统作的功 , Q 为外界传递给
系统的热量.
2. 3 热力学函数的表达式
吉布斯自由能函数展开式为
ΔG =ΔU - TM SM - Pi Ei - ΘS 3 + ∑
j
μj nj
(2)
式中 ,ΔG 是吉布斯自由能改变量 ,ΔU 是内能改变
量 ,μj 表示化学势 , nj 为某一组分某一项的物质的
量. 通过勒让德变换 ,可得到 8 种不同形式的自由能
表达式 ,见表 2[2] .
第 6 期
郭革新等 :关于自由能的一些讨论
19
表 2 8 种不同形式的自由能表达式
及其对应的独立变量
名称
表达式
独立变量
内能
U
S , P , S 3
亥姆霍兹自由能
F = U - ΘS 3
S , P ,Θ
焓
H = U - TM S M - Ei Pi
T , E , S 3
弹性焓
H1 = U - TM S M
T , P , S 3
电焓
H2 = U - Ei Pi
S , E , S 3
吉布斯自由能
G = U - ΘS 3 - TM S M - Ei Pi
T , E ,Θ
弹性吉布斯自由能
G1 = U - ΘS 3 - TM S M
T , P ,Θ
电吉布斯自由能
G2 = U - ΘS 3 - Ei Pi
S , E ,Θ
强度量和广延量是一对对共轭量 ,它们都是场
量 ,若选强度量为自变量(作用量) ,广延量就是感生
量. 单组分单相系统 ,吉布斯自由能就是选取强度量
(Θ, TM , Ei ) 为自变量 ,热力学势的一阶偏导数则是
与之共轭的广延量 ,例如 :熵 S 3
= - 5
G
5Θ
;而热力学
势的二阶偏导数则是物性张量 ,例如 :定压摩尔热容
cp = 5
2
G
5Θ2 =Θ 5 S 3
5Θ p
. 与表 2 对应的 8 个热力学函
数的全微分形式如下(单组分单相系统) :
d U =Θd S 3 + TM d SM + Ei d Pi
d F = - S 3 dΘ+ TM d SM + Ei d Pi
d H =Θd S 3 - SM d TM - Pi d Ei
d H1 =Θd S 3 - SM d TM + Ei d Pi
d H2 =Θd S 3 + TM d SM - Pi d Ei
d G = - S 3 dΘ- SM d TM - Pi d Ei
d G1 = - S 3 dΘ- SM d TM + Ei d Pi
d G2 = - S 3 dΘ+ TM d SM - Pi d Ei
其中 , i = 1 ,2 ,3 ; M = 1 ,2 ,3 ,4 ,5 ,6 ,按爱因斯坦惯
例 ,重复指标意味着求和.
2. 4 一级相变和二级相变的判别
一级和二级相变的判别是看究竟是热力学势的
一阶偏导数突变 ,还是热力学势的二阶偏导数突变 ,
若是一阶偏导数突变 ,则称为一级相变 ;若一阶偏导
数无突变 ,而二阶偏导数突变 ,则称为二级相变.
2. 5 吉布斯自由能 G 的展开式中各项的物理意义
吉布斯自由能函数改变量ΔG 的完整展开式为
ΔG = 外界所作的功 +ΘS 3
外界所作的功 = 极化能 + 应变能 + 磁化能 +
相互作用能
(3)
极化能 = Aij Ei Ej
线性极化能
+
Bijk Ei Ej Ek + Cijkl Ei Ej Ek El + …
高阶非线性极化能
(4)
应变能 = A′MN TM TN + B′MNL TM TN TL +
C′MNL K TM TN TL TK + …= A′ijkl Tij Tkl
线性应变能
+
B′ijklmn Tij Tkl Tmn + C′ijklmnpq Tij Tkl Tmn Tpq + …
高阶非线性应变能
(5)
磁化能 = A″ij Mi Mj
线性磁化能
+
B″ijk Mi Mj Mk + C″ijkl Mi Mj Mk Ml + …
高阶非线性磁化能
(6)
相互作用能应为与压电效应、电致伸缩、压磁效应与
磁致伸缩等效果对应的相互作用能量之和 ,即
dM K TM Ei + qM Kl TM Ek El + …
(7)
式(4) 、(5) 和 (6) 中第一项的系数分别是倒极化率、
弹性劲度系数和磁化强度. 而吉布斯自由能 G 的二
阶偏导都是物性张量 ,即 :
Aij = 5
2
G
5 Ei Ej
=
1
ε0
χ- 1
ij
; Bijk =
53
G
5 Ei 5 Ej 5 Ek
; …
A′MN = CMN =
52
G
5 TM 5 TN
; A′MNL =
53
G
5 TM 5 TN 5 TL
; …
A″MN = BMN = 5
2
G
5 Mi 5 Mj
; B′ijk =
53
G
5 Mi 5 Mj 5 Mk
; …
由式(3) 可以清楚地看出 ,由自由能展开式的一
次项的系数可得出自变量的共轭变量 ;二次项的系
数是线性效应系数 ;三次项的系数是非线性效应系
数. 它们都是物性张量.
2. 6 不考虑相变时 G 的展开式应保留的项数
自由能展开式必须是收敛的(这是 Landau 理论
的假定) . 如果需要研究某个线性物理效应 ,就必须
保留与该物理效应有关的二次项 ;如果需要研究非
线性效应 ,就要保留更高次的项 ;如果需要研究某个
交叉效应 ,就必须保留与该交叉效应有关的二个自
变量的交叉乘积项. 例如 , Sjk = Ei dijk + Ei El Qijkl ,式
中右端的两项分别表示逆压电效应和电致伸缩效
应 , Ei 很大时 ,必须考虑非线性效应 ,就需要保留三
次项乃至四次项.
2. 7 G 的展开式对相变( 特别是连续相变) 的应用
以下以铁电相变为例加以讨论.
G 应是高对称相(高温相) 点群变换的不变量.
因此 ,在式(2) 中保留的非零项 ,应受到群不变量的
制约 , G0 的序参量展开式可以通过其点群的不可约
表示的基函数来构造或通过 Neumann 原理从式(2)
中剔除多余的项来形成.
20
大 学 物 理
第 23 卷
例如 , Td 群(方硼盐) :
1) 按群可约表示其函数来构造不变量.
Td 群(方硼盐) 可构成如下不变式 :
a( x
2
1 + x
2
2 + x
3
2 ) ( A , T 表示的不变式) 二次式
bx1 x2 x3 ( A , T 表示不变式) 三次式
c[ x
4
1 + x
4
2 + x
4
3 - ( x
2
1 x
2
2 + x
2
2 x
2
3 + x
2
3 x
2
1 )]( E
表示不变式) 四次式
d ( x
2
1 x
2
2 + x
2
2 x
2
3 + x
2
3 x
2
1 ) ( T 表示不变式) 四次
式
G = G0 + a( p
2
1 + p
2
2 + p
2
3 ) + b( p1 p2 p3 ) +
c( p
4
1 + p
4
2 + p
4
3 ) + d′( p
2
1 p
2
2 + p
2
2 p
2
3 + p
2
3 p
2
1 )
2) 利用 Neumann 原理 ,剔除张量不变式中的
零项.
Td 群(方硼盐) 生成元( x3 x1 x2 ) ( x1 x2 x3 )
(Aij ) =
A11
0
0
0
A11
0
0
0
A11
=
A1
0
0
0
A1
0
0
0
A1
,A11 = A1 ;
( BiM ) =
0 0 0 B14
0
0
0 0 0
0
B14
0
0 0 0
0
0
B14
,B14 = B123 ;
( CMN ) =
C11
C12
C12
0
0
0
C12
C11
C12
0
0
0
C12
C12
C11
0
0
0
0
0
0
C44
0
0
0
0
0
0
C44
0
0
0
0
0
0
C44
=
C11
C12
C12
0
0
0
C12
C11
C12
0
0
0
C12
C12
C11
0
0
0
0
0
0
C12
0
0
0
0
0
0
C12
0
0
0
0
0
0
C12
( C44 = C2323 = C23 = C12 )
G = G0 + A1 ( p
2
1 + p
2
2 + p
2
3 ) + B14 ( p1 p2 p3 ) +
C11 ( p
4
1 + p
4
2 + p
4
3 ) + C12 ( p
2
1 p
2
2 + p
2
2 p
2
3 + p
2
3 p
2
1 )
其中 A1 = a0 ( T - T0 ) .
对于保留最高次幂的考虑如下 :
①保留的最高次幂必是偶次的而且是正定的 ,
否则 G 就得不到极小值. 考虑到级数展开式是收敛
的 ,一般只取到 6 次幂项.
②由群论可知 ,如果 3 次幂系数为零 ,5 次幂系
数一定为零.
若 3 次幂系数不为零 ,则 G 的展开式保留到 4
次幂项为止即可. 此时可以算得相变是一级的 ;
若 3 次幂系数为零 ,4 次幂系数为正 ,则 G 的
展开式只取到 4 次幂项为止且相变是二级的 ;
若 3 次幂系数为零 ,4 次幂系数小于零 ,则需考
虑 6 次幂项 ,此时相变是一级的. 即 :
G = G0 + Bη2 + Cη3 + Dη4
( B = a0 ( T - T1 ) , a0 >0, C ≠0 , D > 0)
(一级相变)
G = G0 + Bη2 + Dη4
( B = a0 ( T - T1 ) , a0 >0, D > 0)
(二级相变)
G = G0 + Bη2 + Dη4 + Fη6
( B = a0 ( T - T1 ) , a0 >0, D <0, F > 0)
(一级相变)
在以上 3 式中 , G 和 G0 分别表示序参量η不等于零
和等于零时的自由能 ; B , C , D , F 分别表示序参量
η的二、三、四、六次项的系数 ; T1 由 5
2
G
5η2
T = T
1
= 0
得到 ,称为高对称项失稳温度[2~5 ] .
因此 ,相变是一级的还是二级的 ,取决于自由能
展开式的系数. 另外 ,通过调节四次项系数 D 的正
负 ,可达到由一级相变到二级相变的转变[6] . 因此 ,
通过对展开式系数的分析 ,也可直接判定相变是一
级的还是二级的.
2. 8 自由能函数 G 的展开式与 Landau 理论
Landau 理论是研究结构相变的基本理论[3~4 ] ,
它将对称破缺引入结构相变理论 ,并将自由能函数
按序参量的幂级数展开 ,通过求自由能函数的极小
值确定其平衡稳定态. 该理论广泛应用于不同的体
系. 因此 ,对所研究体系的自由能展开式中各项的物
理意义的分析就显得与尤为重要. 对于铁电体 ,长程
力起作用. T =0 K 时 ,关联长度ξ(0) 很长 ,临界区
可以很小 ,在临界区以外的广大区域 ,Landau 理论
都适用. 例如 ,铁电晶体[6~9 ] 、铁电薄膜[ 10 ,11 ] 和向列
相液晶[ 12 ] 等材料.
3 相的稳定性讨论
例如 ,自由能函数 : G = G ( p1 , p2 , p3 ) ,稳定相
自由能取极小 ,即 :
5 G
5 p1=0,5
G
5 p2=0,5
G
5 p3
= 0
第 6 期
郭革新等 :关于自由能的一些讨论
21
于是 , p1 = p 31
, p2 = p 32
, p3 = p 33
,且
52
G
5p
2
1
p 31
, p 32
, p 33
>0,
52
G
5 p
2
1
52
G
5p1 5 p2
52
G
5 p1 5 p2
52
G
5 p
2
2
p 31
, p 32
, p 33
>0
52
G
5 p
2
1
52
G
5 p1 5 p2
52
G
5 p1 5 p3
52
G
5 p1 5 p2
52
G
5 p
2
2
52
G
5 p2 5 p3
52
G
5 p1 5 p3
52
G
5 p2 5 p3
52
G
5 p
2
3
p 31
, p 32
, p 33
> 0
即雅科比(Jacobi) 行列式的顺序主子式均大于零.
4 结论
本文给出了吉布斯自由能的完整展开式 ,式中
各项的物理意义一目了然. 可以看出 , G 和几乎所
有的物理效应相联系. 它的二阶以上偏导就是各个
物理效应的效应系数. 发生相变时 ,相变前后对称性
发生变化. 可能的相可从 G 的一阶偏导等于零求
得. 甚至可直接从自由能展开式中系数的正负 ,来判
断所发生的相变是一级相变 ,还是二级相变. 当用
Landau 理论研究相变时 ,可根据具体情况在自由能
序参量展开式中保留相应的项. 通过相稳定性条件
的讨论 ,可以求出可能的稳定相所存在的温区.
参考文献 :
[1] 陈纲 ,廖理几. 晶体物理学基础[M]. 北京 :科学出版
社 ,1992. 298.
[2] 钟维列. 铁电体物理学[M]. 北京 :科学出版社 ,1998.
69~95.
[3] Landau L D ,Lifshitz E M. Statistical Physics [M]. 3rd
ed. Oxford:Pergamon Press,1980.
[4] Lzyunov Yu A,Syromyatnikov V N. Phase Transitions
and Crystal Symmetry [M]. Dordrecht :Kluwer Publish2
ers ,1990.
[5] 冯端 ,葛庭燧. 金属物理学 :第二卷 相变[M]. 北京 :科
学出版社 ,1990. 44~59.
[6] Stokes H T ,Sadate C ,Hatch D M ,et al. Analysis of the
ferroelectric phase transition in BaAl2 O4 by group theoret2
ical methods and first - principles calculations [J ]. Phys
Rev B ,2002 ,65 :064 105.
[7] Iniguez J ,Ivantchev S ,Perez2Mato J M ,el al. Devonshire
- Landau free energy of BaTiO3 from first principles [J ]
Phys Rev B ,2001 ,63 :114 103.
[8] Oliveira M A S,Gesland J Y,Belo L C M ,el al.
Crystal2
line phase sequence of LiThF7 :A study based on the Lan2
dau theory and linear birefringence measurements [J ].
Phys Rev B ,2000 ,62 :215.
[9] Zhong W L ,Wang Y G,Zhang P L. Landau theory for a
ferroelectric with divertible but irreversible polarization
[J ]. Solid State Commun ,1997 ,101 :815.
[10] Lye2Hock O ,Junaidah O ,Tilley D R. Landau theory of
second - order phase transitions in ferroelectric films
[J ]. Phys Rev B ,2001 ,63 :144 109.
[11] Wang C L ,Zhang L ,Peng Y P ,et al. Landau theory of
asymmetric ferroelectric films under external electric
fields [J ]. Solid State Commun ,1999 ,109 :213.
[12] Moldovan R,Puica M R. Concentration dependence in
the Landau - Gennes theory for nematic lyotropic liquid
crystals [J ]. Phys Lett A ,2001 ,286 :205.
A discussion on free energy
GUO Ge2xin
1 ,2
,ZHOU Guo2xiang
1
,WAN G Ai2kun
1 ,3
,HE Wen2chen
1
(1. School of Sciences ,Hebei University of Technology ,Tianjin 300130 ,China ;2. College of Physics ,Hebei Normal University ,Shiji2
azhuang 050016 ,China ;3. Department of Physics ,Hebei Sciences and Technology University ,Shijiazhuang 050018 ,China)
Abstract :The full expression of free energy is proposed ,and the physical significance of every part of this
expansion are illustrated. The significance of the coefficients of this expansion and that of conjugate variable of
the independent variable are indicated ;i. e. the first order partial differential of Gibbs free energy are thermody2
namics variables ,and the second order partial differential of Gibbs free energy are substance property tensors.
The term numbers of free energy expansions are studied during the phase transition process. Besides ,the stabili2
ty condition of the phase is analyzed.
Key words:free energy ;expansion ;phase transition ;Landau theory
大位能是統計力學中使用的一個量,特別是在開放系統的不可逆過程裡使用。
大位能被定義為
大位能的改變量為
當系統達到熱動力平衡,ΦG有最小值。可以由考慮到當定體積且溫度與化學位停止改變時dΦG為零而見到。
對於理想氣體,
目录[隐藏] |
[编辑] 蘭道自由能
一些作者認為蘭道自由能或蘭道位能是[1][2]
這以羅斯物理學家列夫·朗道命名。取決於系統的規定,這可能是大位能的同義詞。



 ,這裡的F是亥姆霍茲自由能。對於齊次系統,可得
,這裡的F是亥姆霍茲自由能。對於齊次系統,可得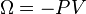
No comments:
Post a Comment