热力学中为什么要引入吉布斯自由能的概念,它的物理含义是什么?
我感觉它是纯数学演算出的。
实在没法找到一个专业的解释,都是千篇一律的公式而已。另,据说玻尔兹曼为了维护他的孤立系统熵增原理而自杀身亡,现在熵增原理被广泛认同了吗?如果是,宇宙的热寂状态终会达到吗?熵增到极大值是个什么概念?那时宇宙还在膨胀吗?如果是,则此熵增将要继续;如果不是,则宇宙膨胀无止境?按照Gibbs自由能原理,当ΔG=0时,达到平衡状态,体系的G降到最小,这个局面终会产生吗?
实在没法找到一个专业的解释,都是千篇一律的公式而已。另,据说玻尔兹曼为了维护他的孤立系统熵增原理而自杀身亡,现在熵增原理被广泛认同了吗?如果是,宇宙的热寂状态终会达到吗?熵增到极大值是个什么概念?那时宇宙还在膨胀吗?如果是,则此熵增将要继续;如果不是,则宇宙膨胀无止境?按照Gibbs自由能原理,当ΔG=0时,达到平衡状态,体系的G降到最小,这个局面终会产生吗?
按投票排序按时间排序
16 个回答
这个问题我都回答了 n 遍了... 这么一个重复问题题主问之前也不搜一下.
怎样直观的理解一般的自由能与吉布斯自由能?
焓的物理意义是什么?
简单而粗略地说, 他们和熵的信息量是一样大的, 只是换了自变量.
另外"实在没法找到一个专业的解释,都是千篇一律的公式而已。"
我觉得在物理学中, 没有公式的专业解释基本上是不靠谱的.
有关宇宙的热寂, 简单地说是因为宇宙是负热容系统, 没有稳定平衡态因此热力学不适用.
参考这个问题:
熵增是否和引力矛盾呢?
怎样直观的理解一般的自由能与吉布斯自由能?
焓的物理意义是什么?
简单而粗略地说, 他们和熵的信息量是一样大的, 只是换了自变量.
另外"实在没法找到一个专业的解释,都是千篇一律的公式而已。"
我觉得在物理学中, 没有公式的专业解释基本上是不靠谱的.
有关宇宙的热寂, 简单地说是因为宇宙是负热容系统, 没有稳定平衡态因此热力学不适用.
参考这个问题:
熵增是否和引力矛盾呢?
内能显示全部, 焓
, 自由能
和
都是自然变量不同的热力学势. 它们都是通过对热力学第一定律的推论(也称热力学基本方程)
做 Legendre 变换得到的.
之所以定义这样的函数就是为了使用方便. 内能的自然变量是
. 它们都是广延量.在实验上, 广延量不容易控制, 而强度量则相对容易. 强度量的定义都是内能
关于其广延量的导数. 如何将
中的广延量改写为强度量而不丢失任何信息呢[1]? Legendre 变换就可以做到这一点. 对于有确定凸性的函数[2], 既可以用其中每一点的坐标
来表示, 也可以用每一点处切线的斜率和截距表示
, 其中
是切线斜率,
是切线截距. 整理得到
, 这就是 Legendre 变换.
自然变量不同的系统服从的热力学基本定律不同. 熵最大原理只适用于孤立系统, 即的系统. 我们还需要找到热力学基本定律在自然变量有强度量的系统中的形式. 有了 Legendre 变换, 这一工作就变得简单得多. 只需要考虑热力学势的全微分式, 如通过
就可以轻易证明 Helmholtz 自由能最小原理: 等温等容系统达到平衡态时 Helmholtz 自由能最小.
总结一下, 引入焓, 自由能
和
之后, 在特定独立变量下能量表达式和热力学定律写起来更简单. 如果硬要理解其物理意义的话, 可以从能量表达式入手. 比如
, 因此等压系统通过膨胀或者热传导向环境传递的能量就是焓变. 类似地, 等温系统在可逆过程中做的功就是系统 Helmholtz 自由能的减小.
[1] 以自然变量为温度和体积的系统为例. 也许有人会 naive 地认为可以直接将改写成
. 但注意到
, 上式实际上是一个
关于
的一阶微分方程. 其解不唯一, 有一个待定常数. 因此直接将
改写成
会丢失信息.
[2] Legendre 变换中对于函数凸性的要求在热力学中是容易满足的. 因为热力学势的凸性对应着系统的稳定性. 如果热力学势没有确定的凸性, 则意味着相变的存在.
------------------------------------update 2014.11.17-------------------------------------------------------------
由于没有很合适的输入公式的工具,所以把文档在latex中编译了,转为图片格式贴在下面。原版的公式看着确实





-----------------------------------------------------------原版------------------------------------------------------------------
这个学期我们组里正好在做非平衡态热力学的讨论班,我和另外一个学长主讲。上周我负责的就是热力学这一部分内容,在雷克那本现代统力学教程(a mordern course in stastical physics)上面讲的很系统,感兴趣可以去看一下。
吉布斯自由能其实是势的一种,就如内能、焓、赫姆霍兹势等一样。所谓势,在物理学中是一种做功的能力,比如我们常见的重力势能,指的是位于 高处的物体在重力作用下存储了一定的能量,而具有做功的能力,通过一定的方式,这种能量能够释放出来转化为对外做功。
吉布斯自由能和众多其他热力学势一样是可以由内能这种势推导出来的,具体为什么可以由它导出以及如何导出我们慢慢分析。
在此之前先介绍一下下面内容将涉及到的热力学基本知识:
热 力学系统基本量:广延量和强度量。广延量指的是随着系统物质的量增加而增大的量,典型的是体积V、内能U、熵S等;强度量顾名思义是与强度有关的 量,比如 压强P、化学能$\miu$等。在数学上的表达为:广延量S,表现为$S(\lambda x)=\lambda S(x)$;强度量P,表现为:$P(\lambda x)=\lambda P(x)$。
我们研究的系统可能涉及到化学能、电磁作用,为了方便起见,我们不考虑系统的化学过程和电磁作用。一般我们接触到的是PVT系统。
进入正题:
先 说内能这种势。学过热力学,显然对它不陌生。由热力学第一定律所谓能量守恒定律,可以知道,热力学系统中是储存着能量的,根据能量 守恒定律我们知道,要想改变内能,要么是通过做功的方式,要么是通过传热的方式,即:$dU=dQ-dW$ 。如果是PV系统,可以写成$dU=dQ-pdV$(dV增大为正,pdV表示的是系统对外做功)。为了方便,半微分也写成全微分形式了,下同。要引入内能的性质,我们还是要引入熵。熵的引入是从卡诺机的热机效率中引出的。所以先介绍一下如何从卡诺机效率引出熵。
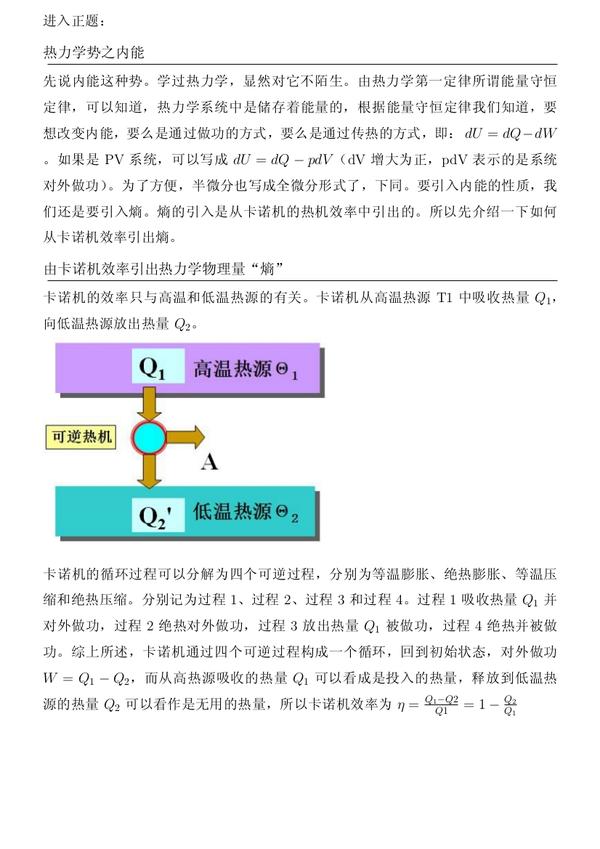
卡诺机的效率只与高温和低温 热源的有关。卡诺机从高温热源T1中吸收热量$Q_1$,向低温热源放出热量$Q_2$。

卡诺机的循环过程可以分解为四个可逆过程,分别为等温膨胀、绝热膨胀、等温压缩和绝热压缩。分别记为过程1、过程2、过程3和过程4。过程1吸收热量$Q_1$并对外做功,过程2绝热对外做功,过程3放出热量$Q_1$被做功,过程4绝热并被做功。综上所述,卡诺机通过四个可逆过程构成一个循环,回到初始状态,对外做功$W=Q_1-Q_2$,而从高热源吸收的热量$Q_1$可以看成是投入的热量,释放到低温热源的热量$Q_2$可以看作是无用的热量,所以卡诺机效率为$\eta=\frac{Q_1-Q2}{Q1}=1-\frac{Q_2}{Q_1}$

可以证明卡诺基效率为$\eta=1-\frac{Q_2}{Q_1}=1-\frac{T_2}{T_1}$。热力学上利用热力学第二定律即所谓热量不能够完全用来做功,可以推导出卡诺机的效率在所有热机中最大即$1-\frac{Q_2}{Q_1}=<1- \frac{T_2} {T_1}$,注意$Q_1$是任一热机从高热源吸收的热量,$Q_2$是该热机释放到低温热源的热量。
由上不等式,我们得 到$\frac{Q_2} {T_2}>=frac{Q_1}{T_1}$。如果我们定义$Q_2$是热机从低温热源的热量,那么显然原不等式中$Q_2$前面需要 加上一个 负号,那么不等式可以改写为:$frac{Q_1}{T_1}+\frac{Q_2}{T_2}<=0$,那么这个不等式得到的就是热机作为一个 系统从两个热源中吸收的热量$Q_1$、$Q_2$与两个热源满足的不等式关系。如果热机从n个热源中吸收 了$Q_1$、$Q_2$、$Q_3$...$Q_n$的热量,可以证明满足不等式:
$\sum_{i=1}^{n}\frac{Q_i} {T_i}<=0$那么对于将热源无穷分下去就有:$\oint \frac{dQ}{dT}<=0$即著名的克劳修斯不等式。
因为卡诺机的是一个可逆过程,所以上式中,当系统经过的过程可逆时,克劳修斯不等式取 等号,即克劳修斯等式$\oint \frac{dQ}{dT}=0$。既然环积分$\oint \frac{dQ}{dT}=0$,那么我们就知道,从状态A到状态B的可逆过程积分$\int_A^B \frac{dQ}{dT}$与路径无关,那么我们就可以定义一种新的物理量,这种量的变化在可逆过程中,与具体的路径无关,无论何种变化方式,只要是可 逆的,该物理量的变化值相同。记这种量为S,叫做熵(entropy)且有$S_A-S_B=\int_A^B\frac{dQ}{dT}$,那 么克劳修 斯不等式可以写成$\oint dS<=0$。假设从A状态,先是经过了一个未知过程,可能可逆,也可能不可逆,到达B状态,然后再经过一个可逆过程回到了A状态,那么整个循环过 程,可能是可逆也可能是不可逆的,所以我们可以得到$\int_A^B\frac{dQ}{dT}+\int_B^A\frac{dQ} {dT}<=0$,所以有$\int_A^B\frac{dQ}{dT}+S_B-S_A<=0$,所以$\int_A^B \frac{dQ}{dT}<=S_A-SB$
当这个循环无限小时,就得到克劳修斯不等式微分形式:$TdS<=dQ$。
结 合内能的微分表达式($dU=dQ-PdV$)可以得到$TdS>=dU+PdV$,把P和V写成一般强度量Y和广延量X的形式(比如对于 电磁系 统,还要考虑除了压强之外的电磁力的作用,所以此处统一用广延量和强度量代替),为:$TdS>=dU-YdX$。
根据这个不等式,我们可以探讨内能的含义。
内能的含义:对于PV系统,在等体等熵条件下,系统内能的减少量是系统对外界做自由功的最大值,同时,在固定的体积和熵条件下,相对于处于 非平衡态的系统,平衡态系统拥有最小的内能。在那个蒸汽时代,我们最关心的是什么?是这个热力学系统能够对外做最大的功是多少,所以自然对于内能和其他各种势的研究层出不穷。以后我 们会看到其他各种势都可以由内能变换得到,并且遵循着同样的规则。
下面我们要证明给出的黑体字所表示的内能的含义。

如图所示系统是绝热系统,系统中气体分为两块,以不绝热但不透气的隔板分开,该系统的总熵与系统总体积保持不变。
$\delta W=\int PdV+ \Delta W_{free}$
对于可逆过程有:
$\Delta U=-\Delta W+\Delta Q$因为绝热,所以有$\Delta Q=0$,且体积不变,所以$\Delta U=-\Delta W_{free}$。所以对于可逆过程,内能的减少恰为对外做自由功的量,内能表现出了势能的意义。
考 虑非可逆过程。以为$TdS>dQ$要保持等熵状态,系统的壁不能再是绝热的。系统实际从外界吸热。 由$dU<=TdS+YdX=TdS- PdV-dW_{free}$,因为等体等熵,所以可以得到$\Delta U<-\Delta W_{free}$。综上所述,当熵和体积固定时,内能的减少时系统对外界做自由功的最大值,同时可以知道,相对于非平衡态,平衡态系统在上述量固定时有 最小内能。
由内能引出其他势的概念。
其实很简单,因为势能依赖于等体等熵条件,看起来才那么表现出势的意义(即潜在的做 自由功的能力),所以我们只要由内能定义出新的量,这个量依赖于S、Y在PV系统中即为S熵和P压强,我们就可以同理推出在等熵等压条件下,这个 量会表现 出势的意义,这个势就是我们常见的焓H。
我们可以推出依赖于T、X,即在PV系统中依赖于温度T和体积V的物理量,在控制等温等体时,该物理量就会表现出势的意义,这个量就是赫姆霍兹势 A。
同理我们可以推出依赖于T、Y,即在PV系统中依赖于温度T和压强P的物理量,在控制等温等压时,该物理量就会表现出势的意义,这个量就是题主感 兴趣的吉布斯自由能。
下面先以焓H为例,来看一看是如何由内能U导出其他势的。
我们定义$H=U-XY$这个变换实际上成为勒让德变换。通过这个变换,我们就将本来依赖于S、X的内能,转换到了依赖于S、Y的物理量H上去。
证明过程如下:
对 上式两边同时取微分,得到$dH=dU-XdY-YdX$,而我们知道$dU=TdS+YdX$,所以$dH=dU-XdY=TdS-XdY$。 显然,是 因为我们把H定义为U减去XY在微分时就得到了dU减去两项,一项是XdY,一项是YdX。而dU中本身就有一个YdX,所以$dH=TdS- XdY$比 较一下与$dU=TdS+YdX$的区别我们就把依赖于S和X的U换成了依赖于S和Y的H,所以,按照U的势的概念,我们同理可以推出:当控制压 强和熵不 变时,$\Delta H<=-\Delta W_{free}$。即所谓:
焓H的含义:对于PV系统,不考虑化学反应,在等压等熵条件下,系统焓的减少量是系统对外界做自由功的最大值,同时,在固定的压强和熵条件 下,相对于处于非平衡态的系统,平衡态系统拥有最小的焓。
所以焓也表现出了势的意义。
同样如果定义赫姆霍兹势A为$A=U-ST$,同理可知$dA=YdX-SdT$,即赫姆霍兹势A依赖于X和T即体积和温度。同样可以得到赫姆霍 兹势A的意义:
焓H的含义:对于PV系统,不考虑化学反应,在等温等体条件下,系统赫姆霍兹势的减少量是系统对外界做自由功的最大值,同时,在固定的体积 和温度条件下,相对于处于非平衡态的系统,平衡态系统拥有最小的赫姆霍兹势。
那么问题来了,对于吉布斯自由能G呢??
显然$G=U-TS-XY$,故,$dG=-SdT-XdY$所以:
焓吉布斯自由能的含义:对于PV系统,不考虑化学反应,在等温等压条件下,系统吉布斯自由能的减少量是系统对外界做自由功的最大值,同时, 在固定的压强和温度条件下,相对于处于非平衡态的系统,平衡态系统拥有最小的吉布斯自由能。
那么吉布斯自由能有什么用?判断化学反应的方向!我 们知道,如果化学反应是发生在大气中,那么化学反应前后应该是一个等温等压的条件,自然界的物质的能量都趋向于向更低的方向发展,所以对于一个系 统化学反 应方程式两边吉布斯自由能小的,其能量状态更低,所以化学反应的方向朝着该方向发展。(这一部分原因想的还不是很充分,欢迎补充)
还没认真校对过,明天要坐火车,现在得出发了,等回去以后再继续更新吧。因为公式看着实在别扭,贴一张编译好的pdf文档吧。 显示全部
由于没有很合适的输入公式的工具,所以把文档在latex中编译了,转为图片格式贴在下面。原版的公式看着确实






-----------------------------------------------------------原版------------------------------------------------------------------
这个学期我们组里正好在做非平衡态热力学的讨论班,我和另外一个学长主讲。上周我负责的就是热力学这一部分内容,在雷克那本现代统力学教程(a mordern course in stastical physics)上面讲的很系统,感兴趣可以去看一下。
吉布斯自由能其实是势的一种,就如内能、焓、赫姆霍兹势等一样。所谓势,在物理学中是一种做功的能力,比如我们常见的重力势能,指的是位于 高处的物体在重力作用下存储了一定的能量,而具有做功的能力,通过一定的方式,这种能量能够释放出来转化为对外做功。
吉布斯自由能和众多其他热力学势一样是可以由内能这种势推导出来的,具体为什么可以由它导出以及如何导出我们慢慢分析。
在此之前先介绍一下下面内容将涉及到的热力学基本知识:
热 力学系统基本量:广延量和强度量。广延量指的是随着系统物质的量增加而增大的量,典型的是体积V、内能U、熵S等;强度量顾名思义是与强度有关的 量,比如 压强P、化学能$\miu$等。在数学上的表达为:广延量S,表现为$S(\lambda x)=\lambda S(x)$;强度量P,表现为:$P(\lambda x)=\lambda P(x)$。
我们研究的系统可能涉及到化学能、电磁作用,为了方便起见,我们不考虑系统的化学过程和电磁作用。一般我们接触到的是PVT系统。
进入正题:
先 说内能这种势。学过热力学,显然对它不陌生。由热力学第一定律所谓能量守恒定律,可以知道,热力学系统中是储存着能量的,根据能量 守恒定律我们知道,要想改变内能,要么是通过做功的方式,要么是通过传热的方式,即:$dU=dQ-dW$ 。如果是PV系统,可以写成$dU=dQ-pdV$(dV增大为正,pdV表示的是系统对外做功)。为了方便,半微分也写成全微分形式了,下同。要引入内能的性质,我们还是要引入熵。熵的引入是从卡诺机的热机效率中引出的。所以先介绍一下如何从卡诺机效率引出熵。
卡诺机的效率只与高温和低温 热源的有关。卡诺机从高温热源T1中吸收热量$Q_1$,向低温热源放出热量$Q_2$。

卡诺机的循环过程可以分解为四个可逆过程,分别为等温膨胀、绝热膨胀、等温压缩和绝热压缩。分别记为过程1、过程2、过程3和过程4。过程1吸收热量$Q_1$并对外做功,过程2绝热对外做功,过程3放出热量$Q_1$被做功,过程4绝热并被做功。综上所述,卡诺机通过四个可逆过程构成一个循环,回到初始状态,对外做功$W=Q_1-Q_2$,而从高热源吸收的热量$Q_1$可以看成是投入的热量,释放到低温热源的热量$Q_2$可以看作是无用的热量,所以卡诺机效率为$\eta=\frac{Q_1-Q2}{Q1}=1-\frac{Q_2}{Q_1}$

可以证明卡诺基效率为$\eta=1-\frac{Q_2}{Q_1}=1-\frac{T_2}{T_1}$。热力学上利用热力学第二定律即所谓热量不能够完全用来做功,可以推导出卡诺机的效率在所有热机中最大即$1-\frac{Q_2}{Q_1}=<1- \frac{T_2} {T_1}$,注意$Q_1$是任一热机从高热源吸收的热量,$Q_2$是该热机释放到低温热源的热量。
由上不等式,我们得 到$\frac{Q_2} {T_2}>=frac{Q_1}{T_1}$。如果我们定义$Q_2$是热机从低温热源的热量,那么显然原不等式中$Q_2$前面需要 加上一个 负号,那么不等式可以改写为:$frac{Q_1}{T_1}+\frac{Q_2}{T_2}<=0$,那么这个不等式得到的就是热机作为一个 系统从两个热源中吸收的热量$Q_1$、$Q_2$与两个热源满足的不等式关系。如果热机从n个热源中吸收 了$Q_1$、$Q_2$、$Q_3$...$Q_n$的热量,可以证明满足不等式:
$\sum_{i=1}^{n}\frac{Q_i} {T_i}<=0$那么对于将热源无穷分下去就有:$\oint \frac{dQ}{dT}<=0$即著名的克劳修斯不等式。
因为卡诺机的是一个可逆过程,所以上式中,当系统经过的过程可逆时,克劳修斯不等式取 等号,即克劳修斯等式$\oint \frac{dQ}{dT}=0$。既然环积分$\oint \frac{dQ}{dT}=0$,那么我们就知道,从状态A到状态B的可逆过程积分$\int_A^B \frac{dQ}{dT}$与路径无关,那么我们就可以定义一种新的物理量,这种量的变化在可逆过程中,与具体的路径无关,无论何种变化方式,只要是可 逆的,该物理量的变化值相同。记这种量为S,叫做熵(entropy)且有$S_A-S_B=\int_A^B\frac{dQ}{dT}$,那 么克劳修 斯不等式可以写成$\oint dS<=0$。假设从A状态,先是经过了一个未知过程,可能可逆,也可能不可逆,到达B状态,然后再经过一个可逆过程回到了A状态,那么整个循环过 程,可能是可逆也可能是不可逆的,所以我们可以得到$\int_A^B\frac{dQ}{dT}+\int_B^A\frac{dQ} {dT}<=0$,所以有$\int_A^B\frac{dQ}{dT}+S_B-S_A<=0$,所以$\int_A^B \frac{dQ}{dT}<=S_A-SB$
当这个循环无限小时,就得到克劳修斯不等式微分形式:$TdS<=dQ$。
结 合内能的微分表达式($dU=dQ-PdV$)可以得到$TdS>=dU+PdV$,把P和V写成一般强度量Y和广延量X的形式(比如对于 电磁系 统,还要考虑除了压强之外的电磁力的作用,所以此处统一用广延量和强度量代替),为:$TdS>=dU-YdX$。
根据这个不等式,我们可以探讨内能的含义。
内能的含义:对于PV系统,在等体等熵条件下,系统内能的减少量是系统对外界做自由功的最大值,同时,在固定的体积和熵条件下,相对于处于 非平衡态的系统,平衡态系统拥有最小的内能。在那个蒸汽时代,我们最关心的是什么?是这个热力学系统能够对外做最大的功是多少,所以自然对于内能和其他各种势的研究层出不穷。以后我 们会看到其他各种势都可以由内能变换得到,并且遵循着同样的规则。
下面我们要证明给出的黑体字所表示的内能的含义。

如图所示系统是绝热系统,系统中气体分为两块,以不绝热但不透气的隔板分开,该系统的总熵与系统总体积保持不变。
$\delta W=\int PdV+ \Delta W_{free}$
对于可逆过程有:
$\Delta U=-\Delta W+\Delta Q$因为绝热,所以有$\Delta Q=0$,且体积不变,所以$\Delta U=-\Delta W_{free}$。所以对于可逆过程,内能的减少恰为对外做自由功的量,内能表现出了势能的意义。
考 虑非可逆过程。以为$TdS>dQ$要保持等熵状态,系统的壁不能再是绝热的。系统实际从外界吸热。 由$dU<=TdS+YdX=TdS- PdV-dW_{free}$,因为等体等熵,所以可以得到$\Delta U<-\Delta W_{free}$。综上所述,当熵和体积固定时,内能的减少时系统对外界做自由功的最大值,同时可以知道,相对于非平衡态,平衡态系统在上述量固定时有 最小内能。
由内能引出其他势的概念。
其实很简单,因为势能依赖于等体等熵条件,看起来才那么表现出势的意义(即潜在的做 自由功的能力),所以我们只要由内能定义出新的量,这个量依赖于S、Y在PV系统中即为S熵和P压强,我们就可以同理推出在等熵等压条件下,这个 量会表现 出势的意义,这个势就是我们常见的焓H。
我们可以推出依赖于T、X,即在PV系统中依赖于温度T和体积V的物理量,在控制等温等体时,该物理量就会表现出势的意义,这个量就是赫姆霍兹势 A。
同理我们可以推出依赖于T、Y,即在PV系统中依赖于温度T和压强P的物理量,在控制等温等压时,该物理量就会表现出势的意义,这个量就是题主感 兴趣的吉布斯自由能。
下面先以焓H为例,来看一看是如何由内能U导出其他势的。
我们定义$H=U-XY$这个变换实际上成为勒让德变换。通过这个变换,我们就将本来依赖于S、X的内能,转换到了依赖于S、Y的物理量H上去。
证明过程如下:
对 上式两边同时取微分,得到$dH=dU-XdY-YdX$,而我们知道$dU=TdS+YdX$,所以$dH=dU-XdY=TdS-XdY$。 显然,是 因为我们把H定义为U减去XY在微分时就得到了dU减去两项,一项是XdY,一项是YdX。而dU中本身就有一个YdX,所以$dH=TdS- XdY$比 较一下与$dU=TdS+YdX$的区别我们就把依赖于S和X的U换成了依赖于S和Y的H,所以,按照U的势的概念,我们同理可以推出:当控制压 强和熵不 变时,$\Delta H<=-\Delta W_{free}$。即所谓:
焓H的含义:对于PV系统,不考虑化学反应,在等压等熵条件下,系统焓的减少量是系统对外界做自由功的最大值,同时,在固定的压强和熵条件 下,相对于处于非平衡态的系统,平衡态系统拥有最小的焓。
所以焓也表现出了势的意义。
同样如果定义赫姆霍兹势A为$A=U-ST$,同理可知$dA=YdX-SdT$,即赫姆霍兹势A依赖于X和T即体积和温度。同样可以得到赫姆霍 兹势A的意义:
焓H的含义:对于PV系统,不考虑化学反应,在等温等体条件下,系统赫姆霍兹势的减少量是系统对外界做自由功的最大值,同时,在固定的体积 和温度条件下,相对于处于非平衡态的系统,平衡态系统拥有最小的赫姆霍兹势。
那么问题来了,对于吉布斯自由能G呢??
显然$G=U-TS-XY$,故,$dG=-SdT-XdY$所以:
焓吉布斯自由能的含义:对于PV系统,不考虑化学反应,在等温等压条件下,系统吉布斯自由能的减少量是系统对外界做自由功的最大值,同时, 在固定的压强和温度条件下,相对于处于非平衡态的系统,平衡态系统拥有最小的吉布斯自由能。
那么吉布斯自由能有什么用?判断化学反应的方向!我 们知道,如果化学反应是发生在大气中,那么化学反应前后应该是一个等温等压的条件,自然界的物质的能量都趋向于向更低的方向发展,所以对于一个系 统化学反 应方程式两边吉布斯自由能小的,其能量状态更低,所以化学反应的方向朝着该方向发展。(这一部分原因想的还不是很充分,欢迎补充)
还没认真校对过,明天要坐火车,现在得出发了,等回去以后再继续更新吧。因为公式看着实在别扭,贴一张编译好的pdf文档吧。 显示全部
首先从熵开始,热力学第二定律的克劳修斯表述告诉我们,对于一个孤立绝热体系(无传热,无传质,无体积变化)的自发过程,其熵变都是大于等于零的。这样用熵这个状态函数就可以很容易地在数学上判定任何孤立绝热体系的演化方向,这个我相信你已经理解了。
但是现实体系大多数都不是孤立绝热的,而多数时候是等温等容(比如控温刚性反应釜中的反应)或是等温等压(比如敞口烧杯中的反应)的。破坏了孤立绝热的条件,单纯用熵变来判定方向就失效了。但是人们又希望能有一个类似于熵的状态函数来帮助我们判定等容或等压反应的方向,那该怎么办呢?方法是假想一个近乎无限大的处于平衡态的环境(E),并使之与你考虑的体系(S)相接触,S本身的体积和能量可以变化,但S只能和E发生体积和能量交换,所以E+S总体上体积和能量都不发生变化,是孤立绝热的,那么就可以针对E+S使用熵增原理分析反应方向。这种分析的结果就导致了两个自由能函数(对于等容体系是赫尔姆兹自由能,对于等压体系是吉布斯自由能)的诞生。具体的推导过程请参见你的热力学课本。简而言之,由于E无限大,E的变化基本可以认为是可逆的,这样环境E的熵变(dS)完全可以通过体系和环境的传热来计算(dQ/T),而dQ又可以通过能量守恒和体系S的内能和体积变化联系起来,所以最终,E+S的总熵变,可以写成一个体系S的熵变以及体系S的内能和体积的函数,这个函数就是自由能。
你现在应该能够理解了,自由能之所以能用于判定等容/等压体系的反应方向,是因为它等价于环境和体系的总熵变(实际上为了让自由能具有能量的量纲,所以在总熵变的前面乘了一个温度T)。那么我们为什么不直接考虑总熵变,而要引入自由能这个量呢?因为直觉告诉我们一个体系的反应方向,应该可以由这个体系本身决定,而和周围环境的具体细节无关,环境E的引入纯粹是分析推导的需要,我们不希望在最终的结果中保留任何关于环境E的具体变量(比如E的熵变)。而自由能(E-TS, E+PV-TS)则纯粹是体系本身的状态函数,在数学上和环境无关,在理论上要漂亮得多,在使用上也方便得多。这就是自由能引入的基本思路,我认为还是很自然的。另外,可以证明自由能还有一个意义,就是它实际上是一个体系在等温等容或等温等压条件下从状态A到状态B,对环境的最大做功,这个显然也是人们在设计热机时非常感兴趣的一个值。
至于你其后的几个问题:熵增原理等价于热力学第二定律,是整个平衡态热力学大厦的基础之一,当然已经被广泛认同。违反热力学第二定律的第二类永动机已经成为公认的伪科学。至于宇宙的问题,这个我就不专业了。如何描述宇宙依然是一个充满争议的问题,但是宇宙肯定不是我们通常意义上所理解的平衡态,所以把平衡态热力学套用在宇宙上的时候必须非常小心。最后再说一句,就算热寂论是对的,你也不能把ΔG套在宇宙上啊?宇宙也许是一个孤立绝热体系,但绝对不是一个等温等压体系啊...
------------------------------------------------------------------------------------------------------------------------------
宇宙什么的我真心不懂,写的肯定一堆错,有行家看到笑一笑就行了,我就不改了,原答案啥样就啥样吧。
但是现实体系大多数都不是孤立绝热的,而多数时候是等温等容(比如控温刚性反应釜中的反应)或是等温等压(比如敞口烧杯中的反应)的。破坏了孤立绝热的条件,单纯用熵变来判定方向就失效了。但是人们又希望能有一个类似于熵的状态函数来帮助我们判定等容或等压反应的方向,那该怎么办呢?方法是假想一个近乎无限大的处于平衡态的环境(E),并使之与你考虑的体系(S)相接触,S本身的体积和能量可以变化,但S只能和E发生体积和能量交换,所以E+S总体上体积和能量都不发生变化,是孤立绝热的,那么就可以针对E+S使用熵增原理分析反应方向。这种分析的结果就导致了两个自由能函数(对于等容体系是赫尔姆兹自由能,对于等压体系是吉布斯自由能)的诞生。具体的推导过程请参见你的热力学课本。简而言之,由于E无限大,E的变化基本可以认为是可逆的,这样环境E的熵变(dS)完全可以通过体系和环境的传热来计算(dQ/T),而dQ又可以通过能量守恒和体系S的内能和体积变化联系起来,所以最终,E+S的总熵变,可以写成一个体系S的熵变以及体系S的内能和体积的函数,这个函数就是自由能。
你现在应该能够理解了,自由能之所以能用于判定等容/等压体系的反应方向,是因为它等价于环境和体系的总熵变(实际上为了让自由能具有能量的量纲,所以在总熵变的前面乘了一个温度T)。那么我们为什么不直接考虑总熵变,而要引入自由能这个量呢?因为直觉告诉我们一个体系的反应方向,应该可以由这个体系本身决定,而和周围环境的具体细节无关,环境E的引入纯粹是分析推导的需要,我们不希望在最终的结果中保留任何关于环境E的具体变量(比如E的熵变)。而自由能(E-TS, E+PV-TS)则纯粹是体系本身的状态函数,在数学上和环境无关,在理论上要漂亮得多,在使用上也方便得多。这就是自由能引入的基本思路,我认为还是很自然的。另外,可以证明自由能还有一个意义,就是它实际上是一个体系在等温等容或等温等压条件下从状态A到状态B,对环境的最大做功,这个显然也是人们在设计热机时非常感兴趣的一个值。
至于你其后的几个问题:熵增原理等价于热力学第二定律,是整个平衡态热力学大厦的基础之一,当然已经被广泛认同。违反热力学第二定律的第二类永动机已经成为公认的伪科学。至于宇宙的问题,这个我就不专业了。如何描述宇宙依然是一个充满争议的问题,但是宇宙肯定不是我们通常意义上所理解的平衡态,所以把平衡态热力学套用在宇宙上的时候必须非常小心。最后再说一句,就算热寂论是对的,你也不能把ΔG套在宇宙上啊?宇宙也许是一个孤立绝热体系,但绝对不是一个等温等压体系啊...
------------------------------------------------------------------------------------------------------------------------------
宇宙什么的我真心不懂,写的肯定一堆错,有行家看到笑一笑就行了,我就不改了,原答案啥样就啥样吧。
解答题主的问题,最核心的概念其实还是熵,直白的语言叫”混乱度“,这是热力学第二定律的基础,理解不了自然就会有无穷多的疑问了。
首先,熵是一个统计概念,它有明确的定义式S=klnΩ,Ω是微观状态数,很显然,当Ω=1时,S=0,这就是说,如果某种物质的微观状态只有一种,那么它的熵就是0,很显然,这种物质只可能在绝对零度的理想中存在(热三定律),而且即使一种物质到了绝对零度,那么由于取向的问题也一样会出现多种微观状态,最经常举的例子就是CO的例子,是取CO还是OC取向的问题。另外,S=klnΩ这个式子还告诉我们,Ω越大,则S越大,直白的语言就是微观状态越多,则熵就越大——我们为了更直观,就把微观状态的数量说成了混乱度。说了这么多,只为说明,熵是有物理意义的,这不是假说,而是和长度、质量、密度一样,所以这不需要我们去相信,而是给我们去使用的。
那么长度、质量和密度我们是可以看得到的,也是可以去测量的,熵是不是也可以?当然也可以。这里就要再举一个非常经典的例子,理想气体的混合问题。相信题主应该已经做过一些这样的题目,等压的两种理想气体会自发混合,它们混合后没有热量的变化,那么现在问题来了,不是哪家强的问题,而是这个过程的动力到底是什么?我们不去想理想气体的问题了好吧,想一想,取一个围棋的棋盘,遮住天元的位置,分别拿出180个白子和黑子,然后随机去摆,摆到最后有没有可能白棋和黑棋各自都是相连的两个整体,而不出现某一片黑棋被白棋分割或者相反?是的,这种情况几乎不可能出现,而这只是180对棋子。那么气体是会运动的,数量又是以10的20多次方计,两种理想气体怎么可能保持分离的状态而不发生混合?这时我和我的小伙伴们都惊呆了,促成理想气体混合的动力,居然,居然尼玛是概率,因为这种两种气体泾渭分明的状态只是所有10的n次方种可能性中的一种,理论上讲,在大概10的好几十次方秒中,有这么一秒钟,这两种气体会重新恢复成两个整体,说白了就是在宇宙开始的时候放一烧瓶混合气体,到2014年可能也观察不到一秒钟两种气体分离的状态,但这个实验却可以让我们感受熵的存在。是的,我们还是看不到熵,但我们回想一下,大气压强这么简单的物理量我们不也看不见么,也是通过一些简单的实验去感受其存在不是么。但是我们也要承认熵确实是一个特殊的物理量,它具有统计学特性,所以如何测量熵就不能简单从定义出发了。
熵在宏观世界中,又被称为热温商,也就是说可以理解成,热/温度,所以看其量纲就可以发现,热是J,而熵是J/K,熵的宏观表现是测量熵值的基础。这个时候就需要说到又一个经典的例子了,卡诺循环。卡诺热机是一个四阶段均可逆的循环过程,最终是将高温热源的能量转移给了低温热源,而整个过程熵变为0,注意一下这时熵的表达式dS=dQ/T,这不就能测量一个过程中的熵变了吗。有了计算熵变的方法,那么就是处理一下熵的零点问题,还记得上面提到的热三定律吧,0点虽然不存在,但是可以作为极限值啊,从一个趋近于0K的温度开始,测量其升温到298K时的熵变,那么这个熵变值就可以近似为该物质298K时的熵值了,就好像测量元素的电离能一样的道理。所以熵是有其宏观表现的,因此也是一个可以测量的物理量。
(再自觉补充一句,当年学习这一段的时候曾有朋友疑问为什么宏观和微观的两个意义不一样的参数能够吻合,其实物理学只是用理论和实验证明了S和lnΩ的正比关系,然后加了一个系数叫k,起名叫玻尔兹曼常数,这种事情很常见,比如人们发现电压U和电流I的关系,然后加了一个系数叫R,还起名叫电阻,嗯,就系酱紫)
熵是一个具体的物理量,而熵判据(熵增原理)则是一个定律,也就是热二定律,这个定律基于现有的研究是正确的,就好像牛顿力学在很长一段时间里也都是正确的,只有当我们的认识逐步深化,才会逐步发现现有定律的不足。现代科学还是承认热二定律的,目前似乎也没有修正的必要。
熵增原理能不能应用到全宇宙,这个不好说,以人的能力,暂时还看不透宇宙算是啥系统,就算是孤立绝热系统,谁也说不好这么大个的系统是不是也适用人类这点认识。庄子曾提到过一种不知道有冬天的虫子,因为它们的寿命仅春夏秋三季而已,对宇宙而言,现在的人类还不如这虫子呢。
至于吉布斯自由能与熵的关系, @余旷的答案里多有涉及,本质上就是解决了ΔH不为0时的熵判据问题,既然S有意义,H也有意义,那么G=H-TS这个表达式也是有物理意义的,吉布斯自由能当然也就有意义了。
补充一句焓的物理学意义,H的定义是内能与外功的和,但内能按照现在的条件委实是难以给出绝对值,就和早期的温度物理量一样,只有摄氏度,所以就人为定义了0点,也就是稳定单质的标准生成焓为0,类似的,稳定单质的标准生成吉布斯自由能也人为确定为0,这不是因为它们没有绝对值,而是目前的热力学领域只能这么处理,而ΔH和ΔG已经可以用来解决主要问题。
私以为,S的物理学意义其实比物质的量n这个物理量要更物理一些,实际上mol这个量纲就是分子的个数不是么,这尼玛才真叫纯数学演算呢,一个数字,凑到10的23次方就叫物理量了,还是七大基本物理量——不过化学计算确实离不开n倒也是真的了 显示全部
首先,熵是一个统计概念,它有明确的定义式S=klnΩ,Ω是微观状态数,很显然,当Ω=1时,S=0,这就是说,如果某种物质的微观状态只有一种,那么它的熵就是0,很显然,这种物质只可能在绝对零度的理想中存在(热三定律),而且即使一种物质到了绝对零度,那么由于取向的问题也一样会出现多种微观状态,最经常举的例子就是CO的例子,是取CO还是OC取向的问题。另外,S=klnΩ这个式子还告诉我们,Ω越大,则S越大,直白的语言就是微观状态越多,则熵就越大——我们为了更直观,就把微观状态的数量说成了混乱度。说了这么多,只为说明,熵是有物理意义的,这不是假说,而是和长度、质量、密度一样,所以这不需要我们去相信,而是给我们去使用的。
那么长度、质量和密度我们是可以看得到的,也是可以去测量的,熵是不是也可以?当然也可以。这里就要再举一个非常经典的例子,理想气体的混合问题。相信题主应该已经做过一些这样的题目,等压的两种理想气体会自发混合,它们混合后没有热量的变化,那么现在问题来了,不是哪家强的问题,而是这个过程的动力到底是什么?我们不去想理想气体的问题了好吧,想一想,取一个围棋的棋盘,遮住天元的位置,分别拿出180个白子和黑子,然后随机去摆,摆到最后有没有可能白棋和黑棋各自都是相连的两个整体,而不出现某一片黑棋被白棋分割或者相反?是的,这种情况几乎不可能出现,而这只是180对棋子。那么气体是会运动的,数量又是以10的20多次方计,两种理想气体怎么可能保持分离的状态而不发生混合?这时我和我的小伙伴们都惊呆了,促成理想气体混合的动力,居然,居然尼玛是概率,因为这种两种气体泾渭分明的状态只是所有10的n次方种可能性中的一种,理论上讲,在大概10的好几十次方秒中,有这么一秒钟,这两种气体会重新恢复成两个整体,说白了就是在宇宙开始的时候放一烧瓶混合气体,到2014年可能也观察不到一秒钟两种气体分离的状态,但这个实验却可以让我们感受熵的存在。是的,我们还是看不到熵,但我们回想一下,大气压强这么简单的物理量我们不也看不见么,也是通过一些简单的实验去感受其存在不是么。但是我们也要承认熵确实是一个特殊的物理量,它具有统计学特性,所以如何测量熵就不能简单从定义出发了。
熵在宏观世界中,又被称为热温商,也就是说可以理解成,热/温度,所以看其量纲就可以发现,热是J,而熵是J/K,熵的宏观表现是测量熵值的基础。这个时候就需要说到又一个经典的例子了,卡诺循环。卡诺热机是一个四阶段均可逆的循环过程,最终是将高温热源的能量转移给了低温热源,而整个过程熵变为0,注意一下这时熵的表达式dS=dQ/T,这不就能测量一个过程中的熵变了吗。有了计算熵变的方法,那么就是处理一下熵的零点问题,还记得上面提到的热三定律吧,0点虽然不存在,但是可以作为极限值啊,从一个趋近于0K的温度开始,测量其升温到298K时的熵变,那么这个熵变值就可以近似为该物质298K时的熵值了,就好像测量元素的电离能一样的道理。所以熵是有其宏观表现的,因此也是一个可以测量的物理量。
(再自觉补充一句,当年学习这一段的时候曾有朋友疑问为什么宏观和微观的两个意义不一样的参数能够吻合,其实物理学只是用理论和实验证明了S和lnΩ的正比关系,然后加了一个系数叫k,起名叫玻尔兹曼常数,这种事情很常见,比如人们发现电压U和电流I的关系,然后加了一个系数叫R,还起名叫电阻,嗯,就系酱紫)
熵是一个具体的物理量,而熵判据(熵增原理)则是一个定律,也就是热二定律,这个定律基于现有的研究是正确的,就好像牛顿力学在很长一段时间里也都是正确的,只有当我们的认识逐步深化,才会逐步发现现有定律的不足。现代科学还是承认热二定律的,目前似乎也没有修正的必要。
熵增原理能不能应用到全宇宙,这个不好说,以人的能力,暂时还看不透宇宙算是啥系统,就算是孤立绝热系统,谁也说不好这么大个的系统是不是也适用人类这点认识。庄子曾提到过一种不知道有冬天的虫子,因为它们的寿命仅春夏秋三季而已,对宇宙而言,现在的人类还不如这虫子呢。
至于吉布斯自由能与熵的关系, @余旷的答案里多有涉及,本质上就是解决了ΔH不为0时的熵判据问题,既然S有意义,H也有意义,那么G=H-TS这个表达式也是有物理意义的,吉布斯自由能当然也就有意义了。
补充一句焓的物理学意义,H的定义是内能与外功的和,但内能按照现在的条件委实是难以给出绝对值,就和早期的温度物理量一样,只有摄氏度,所以就人为定义了0点,也就是稳定单质的标准生成焓为0,类似的,稳定单质的标准生成吉布斯自由能也人为确定为0,这不是因为它们没有绝对值,而是目前的热力学领域只能这么处理,而ΔH和ΔG已经可以用来解决主要问题。
私以为,S的物理学意义其实比物质的量n这个物理量要更物理一些,实际上mol这个量纲就是分子的个数不是么,这尼玛才真叫纯数学演算呢,一个数字,凑到10的23次方就叫物理量了,还是七大基本物理量——不过化学计算确实离不开n倒也是真的了 显示全部
Brook Lee 赞同
G=H-TS,就是个状态函数,引入它就是因为它在讨论许多问题的时候非常好用。历史上还出现过许多其他的状态函数,但是因为没什么用就又被放弃了。
熵增没什么疑问,但是热寂不一定,主要因为把宇宙当成一个系统直接套函数显得不是很靠谱,比如现在热衷寻找的暗物质,到底会不会导致宇宙无限膨胀下去还是到了临界点再收缩等等。
熵增没什么疑问,但是热寂不一定,主要因为把宇宙当成一个系统直接套函数显得不是很靠谱,比如现在热衷寻找的暗物质,到底会不会导致宇宙无限膨胀下去还是到了临界点再收缩等等。
我读书少 赞同
其实物理量的物理意义都是人为赋予的,引入某一物理量大多是为了更好的解释物理现象或者是更好的进行量化计算。G的单位是什么?J,竟然是能量单位?那么我们是不是可以将其理解为一种特殊能量?干嘛用的?指明变化方向啊。为嘛荷叶上的水滴是球状?表面G,最小啊。为什么会发生化学变化?G,变小啊?这样回答似乎在耍流氓,但是你要想它怎么变小呢?不要只看到公式,要看到公式背后的现象。不等号是什么,不等号表示的是方向,等号是什么?等号表示的是平衡?熵增原理是有条件的,热寂说他所谓的系统可以看做孤立的嘛?房间脏了总会被打扫,有人犯罪但还有的会被抓。毕竟房间不会成为垃圾场, 小偷不会无休止增加。玻尔兹曼自杀是他的问题,总认为自己不被接受,学生听不懂他的理论,其实现在研究生听懂课确实不很多吧。先这样,睡觉。
平衡时ΔG=0 无误。。这个条件当然可以达到了。。。但注意的是一般说ΔG=0是针对某一个反应,而不能是几个反应,或还有其他物理化学变化
自由能是为了解决在一定条件下的化学反应的“自发性”(也可以理解为'"可行性")而定义的概念。人们发现,反应自发与否,不能单纯的凭借焓或熵来定义,于是为了从能量角度来定义反应的“可行性,吉布斯发现了自由能的概念。自由能和电场中的电势类似,纯属于定义出来的概念。
熵增原理显然已经不是假说了,热力学第二定律和本质就是熵增吧。宇宙热寂现在只能演算一下(不是学物理的不知道演算到什么程度了)宇宙膨胀的话,要基于宇宙大爆炸的假说,这个,还只是假说是不是?
自由能是为了解决在一定条件下的化学反应的“自发性”(也可以理解为'"可行性")而定义的概念。人们发现,反应自发与否,不能单纯的凭借焓或熵来定义,于是为了从能量角度来定义反应的“可行性,吉布斯发现了自由能的概念。自由能和电场中的电势类似,纯属于定义出来的概念。
熵增原理显然已经不是假说了,热力学第二定律和本质就是熵增吧。宇宙热寂现在只能演算一下(不是学物理的不知道演算到什么程度了)宇宙膨胀的话,要基于宇宙大爆炸的假说,这个,还只是假说是不是?
这个其实叫做吉布斯自由能量公式--Gibbs free-energy equation!
G=H-TS. H是焓。S是熵—一种描述混乱程度的量(虽然有点抽象但这是定义)G=0没有和反应
G小于0就会有自主反应spontaneous reaction
G大于0时不会发生自主反应
T为绝对温度
G=H-TS. H是焓。S是熵—一种描述混乱程度的量(虽然有点抽象但这是定义)G=0没有和反应
G小于0就会有自主反应spontaneous reaction
G大于0时不会发生自主反应
T为绝对温度
等温、等压的封闭体系内,不作非体积功的前提下,任何自发反应总是朝着吉布斯自由能(G)减小的方向进行。ΔG=0时,反应达平衡,体系的G降到最小值。
叉,这不就是物理含义嘛,很直观了。你要习惯从变化量倒推回状态量,从状态量分析出不变量,这才是物理式的思维方式呀。先看到静后看到变是受限的朴素自然,为毛不能先看到变再明白静呢?
叉,这不就是物理含义嘛,很直观了。你要习惯从变化量倒推回状态量,从状态量分析出不变量,这才是物理式的思维方式呀。先看到静后看到变是受限的朴素自然,为毛不能先看到变再明白静呢?
以我目前尚不全面的感知,我认为自然科学的尽头是哲学,自然科学中的规律定理都有其适用条件与量变范围,哲学告诉我们量变超过承受必然导致质变,质变后的下一量变范围必然不再适用于之前的规律。所以把熵增推广到宇宙应该还有很多地方需要考虑。吉布斯自由能没有什么需要明确的物理意义,很多时候物理意义让理解变的深刻,但也禁锢了对其的进一步理解。对于数学式引入的吉布斯自由能,很大部分是为了分析一些具体问题的方便。其中化学势(偏摩尔吉布斯自由能)在应用上更方便。对于一个无非体积功的过程,比较前后化学势大小(有乘对应计量数),也就是比较摩尔过程或反应的吉布斯自由能的大小可以明确变化方向,在电化学和其它可应用系统输出非体力功的过程,前后摩尔过程或反应吉布斯自由能的变化中可得到最大理想输出量,这个时候的吉布斯自由能很像是一种系统具有的能量(只是像,我们都知道它不是系统的能量),又因为它具有能量量纲,才最后冠以能的名称。







No comments:
Post a Comment