向量积只存在于三维向量中? | 问答| 问答| 果壳网科技有意思
www.guokr.com/question/510522/
轉為繁體網頁
为什么矩阵的行秩/列秩= 用秩一矩阵和逼近的最小项数 ... - 知乎
www.zhihu.com/question/25524419
轉為繁體網頁
三维空间已知张成一个平面的两个不平行向量,求法向量_百度知道
zhidao.baidu.com › 教育/科学 › 理工学科 › 数学
轉為繁體網頁
向量外积与行列式的本质关系| 数学笔记
math.tianpeng.org/2010/04/向量外积与行列式的本质关系/
轉為繁體網頁
【线性代数的几何意义】向量的基本几何意义- AndyJee - 博客园
www.cnblogs.com/AndyJee/p/3491458.html
轉為繁體網頁
[PDF]行列式几何化的教学研究
www.paper.edu.cn/index.../1674-5884(2012)04-0090-05
轉為繁體網頁
《线性代数》 - longhuihu的专栏- 博客频道- CSDN.NET
blog.csdn.net/longhuihu/article/category/1887589
轉為繁體網頁
[PDF]基于Clifford 代数的混合型传感器网络覆盖理论分析
info.scichina.com:8083/sciF/.../downloadArticleFile.do?...
轉為繁體網頁
何 ... 外积是一个二向量( 平面量) , 即这两个向量张成的平面内的. 一个有方向的面积 ...
向量外积与行列式的本质关系
在三维空间中,两个向量a和b的外积a×b定义为这样的一个向量:
1) |a×b|=|a||b|sin<a,b> 其中sin<a,b>表示a和b两向量夹角的正弦。
2) 若|a×b|≠0,那么a×b的方向垂直于a和b所在平面并且使a,b,c满足右手螺旋定则。
设i,j,k是三维空间中成右手定则关系的标准正交基底,a和b在这组基底下的坐标分别为(a1,a2,a3)和(b1,b2,b3),那么a×b可以用行列式形式地表示为
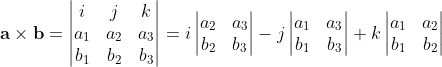
这个公式的由来,在一般的教材中,是先推导出外积的几个重要性质:
1) a×b = -b×a
2) (a+b)×c = a×c+b×c
3) a×(b+c) = a×b+a×c
4) a×(kb)=(ka)×b=k(a×b)
5) i×j=k,j×k=i,k×i=j
然后,就可以利用这些性质对以下式子进行展开:
a×b=(a 1 i+a 2 j+a 3 k)×(b 1 i+b 2 j+b 3 k)
最后化为上面的行列式表示。
但是,为什么外积可以如此规整地表示为一个行列式?难道只是巧合吗?一定有某些内在的原因。
设
c=(∣ ∣ ∣ a 2 b 2 a 3 b 3 ∣ ∣ ∣ ,−∣ ∣ ∣ a 1 b 1 a 3 b 3 ∣ ∣ ∣ ,∣ ∣ ∣ a 1 b 1 a 2 b 2 ∣ ∣ ∣ )
首先,注意到 c 的三个分量是那个三阶行列式中的三个子式,利用行列式展开法则,我们可以很容易地证明c垂直于a和b:
c⋅a =a 1 ∣ ∣ ∣ a 2 b 2 a 3 b 3 ∣ ∣ ∣ −a 2 ∣ ∣ ∣ a 1 b 1 a 3 b 3 ∣ ∣ ∣ +a 3 ∣ ∣ ∣ a 1 b 1 a 2 b 2 ∣ ∣ ∣ =∣ ∣ ∣ ∣ a 1 a 1 b 1 a 2 a 2 b 2 a 3 a 3 b 3 ∣ ∣ ∣ ∣ =0
c⋅b =b 1 ∣ ∣ ∣ a 2 b 2 a 3 b 3 ∣ ∣ ∣ −b 2 ∣ ∣ ∣ a 1 b 1 a 3 b 3 ∣ ∣ ∣ +b 3 ∣ ∣ ∣ a 1 b 1 a 2 b 2 ∣ ∣ ∣ =∣ ∣ ∣ ∣ b 1 a 1 b 1 b 2 a 2 b 2 b 3 a 3 b 3 ∣ ∣ ∣ ∣ =0
那么,为了证明c就是a×b,我们还需证明 |c|=|a||b|sin<a,b> ,以及a,b,c满足右手螺旋定则。
为了证明三个向量a=(a1,a2,a3),b=(b1,b2,b3),c=(c1,c2,c3)满足右手螺旋定则,只需验证行列式
| a1 a2 a3 |
| b1 b2 b3 |
| c1 c2 c3 |
的值是非负的。为此,我们将c的坐标代入,并把此行列式按c的那一行展开,得到行列式的值等于 |c| ² ,因此它确实是非负的。
下面证明|c|=|a||b|sin<a,b> 。考虑行列式
| a1 a2 a3 |
| b1 b2 b3 |
| c1 c2 c3 |
的几何意义,知道它是a,b,c三个向量组成的平行六面体的体积,前面我们已经知道它的数值等于 |c| ² 。又因为c垂直于a和b,那么下面的式子是成立的:
|c| ² =|a| |b| sin<a,b> |c| (因为体积等于底面积乘以高)
当c≠0时,我们直接可以得到 |c| =|a| |b| sin<a,b>。
当c=0时,我们任意取一个三维向量d=(d1,d2,d3),考虑行列式
| a1 a2 a3 |
| b1 b2 b3 |
| d1 d2 d3 |
因为它总是0,即不论d是什么向量,a,b,d总是线性相关。我们可以断定a,b线性相关,从而|a| |b| sin<a,b>=0,同样有|c| =|a| |b| sin<a,b>。
这样,没有用到外积的那些难以推导的性质,直接用行列式的性质,我们就证明了上面的外积表达式,而且这个证明更能揭示它们之间的本质联系。
因为有这样的本质联系,我们可以把三维空间中两个向量的外积推广到n维空间中的n-1个向量的情形。但是需要注意的是向量的顺序与定向的问题:如果规定
a1,a2, ...,an-1,a1×a2×...an-1取正向,那么必须在表示外积的行列式中把基底那一行写在最下面,然后按照基底那一行展开成各个分量。
在初级线性代数中,有几个概念之间有密切联系,这些概念是:
1)行列式,2)3个向量张成多面体的有向体积,3)2个向量的外积,4)3个向量的混合积
其实1,2,4直接相等,证明的途径多种多样,这里列出了一种,与一般的教科书稍有不同,即先承认1)等于2),再由此推出3)的表达式,最后推得4)等于1)。
其实承认1)等于2)之后,4)等于1)是很自然的(根据外积和混合积的定义),然后用类似上文的方法也可以推出3)的表达式。
如果开始像一般的线性代数书那样推导3)的表达式,那么4)等于1)就是显然的,从而可以证明1)等于2)。
这些内容都可以向高维空间推广,这里就不赘述了。
1) |a×b|=|a||b|sin<a,b> 其中sin<a,b>表示a和b两向量夹角的正弦。
2) 若|a×b|≠0,那么a×b的方向垂直于a和b所在平面并且使a,b,c满足右手螺旋定则。
设i,j,k是三维空间中成右手定则关系的标准正交基底,a和b在这组基底下的坐标分别为(a1,a2,a3)和(b1,b2,b3),那么a×b可以用行列式形式地表示为
这个公式的由来,在一般的教材中,是先推导出外积的几个重要性质:
1) a×b = -b×a
2) (a+b)×c = a×c+b×c
3) a×(b+c) = a×b+a×c
4) a×(kb)=(ka)×b=k(a×b)
5) i×j=k,j×k=i,k×i=j
然后,就可以利用这些性质对以下式子进行展开:
最后化为上面的行列式表示。
但是,为什么外积可以如此规整地表示为一个行列式?难道只是巧合吗?一定有某些内在的原因。
设
首先,注意到 c 的三个分量是那个三阶行列式中的三个子式,利用行列式展开法则,我们可以很容易地证明c垂直于a和b:
那么,为了证明c就是a×b,我们还需证明 |c|=|a||b|sin<a,b> ,以及a,b,c满足右手螺旋定则。
为了证明三个向量a=(a1,a2,a3),b=(b1,b2,b3),c=(c1,c2,c3)满足右手螺旋定则,只需验证行列式
| a1 a2 a3 |
| b1 b2 b3 |
| c1 c2 c3 |
的值是非负的。为此,我们将c的坐标代入,并把此行列式按c的那一行展开,得到行列式的值等于 |c| ² ,因此它确实是非负的。
下面证明|c|=|a||b|sin<a,b> 。考虑行列式
| a1 a2 a3 |
| b1 b2 b3 |
| c1 c2 c3 |
的几何意义,知道它是a,b,c三个向量组成的平行六面体的体积,前面我们已经知道它的数值等于 |c| ² 。又因为c垂直于a和b,那么下面的式子是成立的:
|c| ² =|a| |b| sin<a,b> |c| (因为体积等于底面积乘以高)
当c≠0时,我们直接可以得到 |c| =|a| |b| sin<a,b>。
当c=0时,我们任意取一个三维向量d=(d1,d2,d3),考虑行列式
| a1 a2 a3 |
| b1 b2 b3 |
| d1 d2 d3 |
因为它总是0,即不论d是什么向量,a,b,d总是线性相关。我们可以断定a,b线性相关,从而|a| |b| sin<a,b>=0,同样有|c| =|a| |b| sin<a,b>。
这样,没有用到外积的那些难以推导的性质,直接用行列式的性质,我们就证明了上面的外积表达式,而且这个证明更能揭示它们之间的本质联系。
因为有这样的本质联系,我们可以把三维空间中两个向量的外积推广到n维空间中的n-1个向量的情形。但是需要注意的是向量的顺序与定向的问题:如果规定
a1,a2, ...,an-1,a1×a2×...an-1取正向,那么必须在表示外积的行列式中把基底那一行写在最下面,然后按照基底那一行展开成各个分量。
在初级线性代数中,有几个概念之间有密切联系,这些概念是:
1)行列式,2)3个向量张成多面体的有向体积,3)2个向量的外积,4)3个向量的混合积
其实1,2,4直接相等,证明的途径多种多样,这里列出了一种,与一般的教科书稍有不同,即先承认1)等于2),再由此推出3)的表达式,最后推得4)等于1)。
其实承认1)等于2)之后,4)等于1)是很自然的(根据外积和混合积的定义),然后用类似上文的方法也可以推出3)的表达式。
如果开始像一般的线性代数书那样推导3)的表达式,那么4)等于1)就是显然的,从而可以证明1)等于2)。
这些内容都可以向高维空间推广,这里就不赘述了。
No comments:
Post a Comment