phymath999: 双曲型方程，扰动一点，只影响下游一部分（想想马赫锥）,双曲型方程，扰动一点，只影响下游一部分（想想马赫锥）

Wednesday, April 1, 2015

双曲型方程，扰动一点，只影响下游一部分（想想马赫锥）,双曲型方程，扰动一点，只影响下游一部分（想想马赫锥）

流体力学中定常问题为什么要用非定常的方法解答？修改

写补充说明

添加评论 • 邀请回答

按投票排序按时间排序

7 个回答

黄大宁，航空/Linux/创造

收起

Ang Li、Zhu Roger、小小熊等人赞同

搞过一点，来简单说一下。错漏的请各位补充。

举例来说，考虑一个翼型的跨音速流场。该流场内会同时存在亚音速和超音速流场，比如这个，
[SINUMEF Lab] Transonic buffet over a supercritical airfoil
图中红色区域为亚音速，剩下的是超音速。（这个图实际上讲的是buffet，不过关系不大）。由于控制方程性质不同，数值格式上的处理比较麻烦。如果在定常的方程里加入一个时间项，那么控制方程将变成纯的双曲方程，可以按统一的格式求解。并且，由于稳态前的流场通常不是我们感兴趣的部分，可以用较大的时间步来达到收敛状态，而不需关注收敛过程中的精度。如果本身是个非定常问题，那么可以加入伪时间步，达到每个时间步的收敛（这个具体没做过，但是大致是这个思路）。

具体来说，这两种流场的控制方程，亚音速的是椭圆型的，即流场中的扰动会向四周传播；超音速的是双曲型的，即流场中的扰动只向下游传播。或许看一个简单的方程比较清楚，
Potential flow
中间有一个线化小扰动势流方程，可见M<1时这是个椭圆型方程，M>1时是个双曲型方程。

对于不同类型的方程，设计数值格式时要满足不同的要求。一个合理的格式应该满足基本条件，Lax equivalence theorem，体现在这里是要满足CFL数的要求，具体见Courant。这个有点抽象，具体来看例子。

这里涉及的主要是影响区/依赖区的问题。椭圆型方程，如上提到的，扰动一点，影响全场；一点的解也依赖于全场。相应的数值格式要模拟这种特性，比如用中心差分格式，利用周围所有的点来更新当前的点。（Central differencing scheme）。双曲型方程，扰动一点，只影响下游一部分（想想马赫锥），相应的数值格式常常选上风类的，简单来说，对于一维情况，就是当前流动来自左方，就用左边的点差分；反之用右边的点。（Upwind scheme）。
对于实际的流场，不知道哪里会出现亚音速、哪里出现超音速，那么就不能确定哪里用什么格式。要知道的一点是，用错格式会导致发散。或许可以根据当地马赫数判断，但是这会很繁琐。
如果加入时间项，想象加入一个时间维，有点像这个Light cone。那么即使是椭圆型方程，也出现了有限的影响区/依赖区，如双曲型方程一样。于是可以统一求解。

以上的思路是有限差分法，放到更常用的有限体积法来说，加入时间项，可以构成一个守恒型系统（因为对应的物理意义是质量、动量、能量守恒）。同时，由于这个系统有求解弱解的需要（说白了就是激波这样的间断，导致流场不能用光滑的解来描述），涉及Riemann problem的求解。当前已经有很多可靠的黎曼求解器，比如Roe, AUSM等等。那么，在将椭圆型方程统一到守恒型系统后，可以直接用这些求解器来求解流场。

-----------------------------------------------------------------------------
2014/06/09 更新

最近做了一个跨音速翼型的算例，应该算CFD的入门case。想起来这里答过这么个问题，就放上来参考一下。

翼型：NACA0012，来流：马赫数0.8，攻角1.25度。求解欧拉方程，使用有限体积法的Roe格式，做一阶时间推进。

欧拉方程参考Euler equations (fluid dynamics)中Conservation and vector form这节的形式。这边精确解应该满足的定常二维情况的控制方程应该是，
$\frac{\partial F(U)}{\partial x}+\frac{\partial G(U)}{\partial y}=0$
和wiki略不同，这边的表达式里面U是流场变量（的守恒形式），F和G是通量。为简化描述，记左边为 $R(U)$ ，称为残差。
转到非定常的描述，控制方程变为，
$\frac{\partial U}{\partial t}+R(U)=0$
显然， $R(U)=0$ 是满足这个方程的，而在近似解不精确满足定常方程时，我们有 $\frac{\partial U}{\partial t}=-R(U)\neq 0$ ，也就是说知道离准确解相差多少，基于此可以向其修正。当然，更重要的是，加入时间项以后，方程双曲化，在做了时间离散后，就可以轻松地用上面提到的方法来求解了。
（说明，实际上F，G，U，0这些都应该是向量，该用粗体，我偷懒了。）

在做这个问题时，我还用了一些技巧，就是网格自适应。这里用了三角形网格，在时间推进途中，每隔一定时间，我找到流场某些变量梯度比较大的地方，对当地网格进行加密，插值分配新单元的值，继续做时间推进。这样可以在保证一定计算效率的前提下，大大提高激波分辨率。

以下是网格没加密前时的网格和马赫数分布，可见上翼面激波存在，但是被平滑得比较严重：

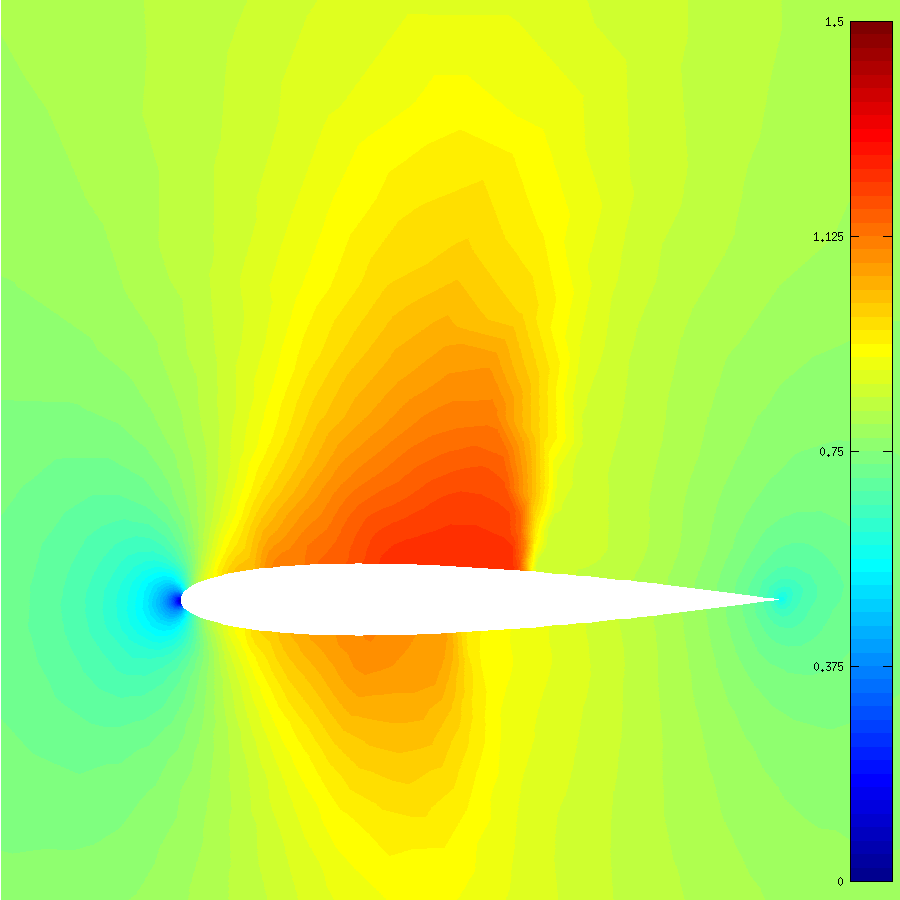在经过13次网格自适应加密后，新的网格和最终的解如下：

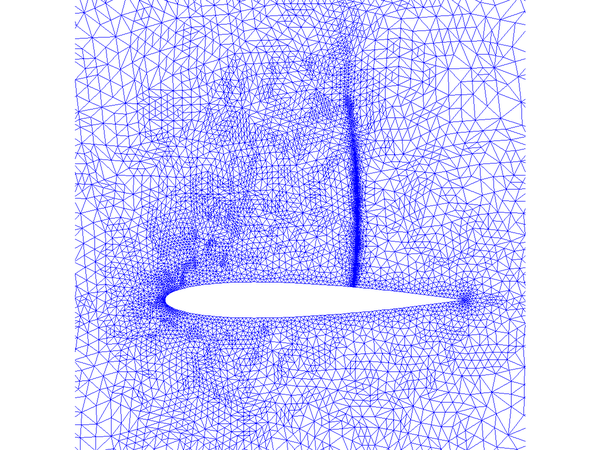
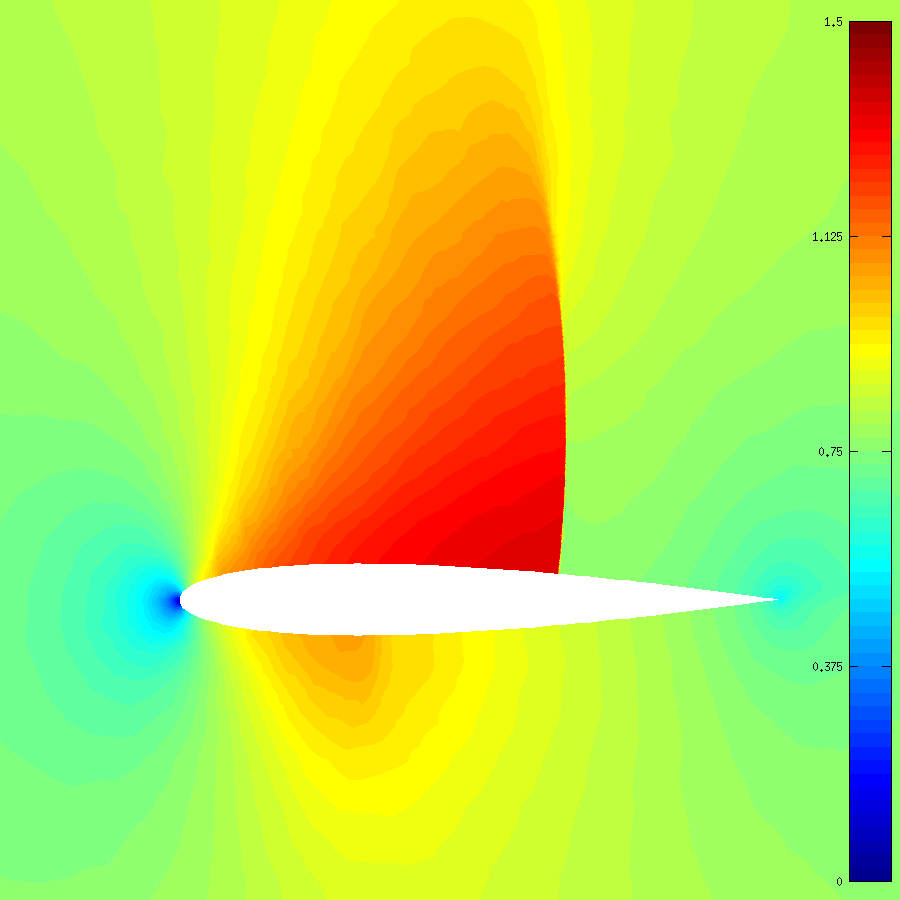实际上光看网格疏密就知道激波在哪里了，流场里面，激波间断十分明显，效果不错。

编辑于 2014-06-10 3 条评论感谢分享收藏 • 没有帮助 •

高木端，面向飞行器设计的计算流体力学，也即空气…

收起

GearDing、黄大宁赞同

真正麻烦的根源是非线性，时间推进只不过是迭代的另一个名字。

－－
三八节略有闲情，补点解释。

我们可以把流体力学问题抽象成已知函数F，求u满足
$F(u)+r=0$
的问题。并且，很重要的一点，F对u是非线性的，也就是说如果 $\lambda \ne 0$ 那么 $F(\lambda u)\ne \lambda F(u)$ .

太抽象了对吧，打个比方：
求 x 使得 5x+8=0. 这个简单， $x=5^{-1}\times (-8)$ －－这是线性问题，我们知道怎么求逆。
进一步，求 $x\in[0,\infty)$ 使得 $5x^2+8=0$ . 就没那么方便了。别说你会笔算开平方！如果你仔细想，所有的开方算法中都包含“试”的元素，没有直接算法的。

这时候怎么办呢？我们先选个初值 $x_0$ ,一般是不对的。这时候我们要过某种方法算出来个 $\delta x_0$ ,叠加到 $x_0$ 上得到 $x_1$ : $x_1=x_0+\delta x_0$ .一直重复这个过程直到 $\delta x_n$ 足够小。这就是我们对付非线性问题的思路。即使这样，最后能不能得到一个稳定的 $x_n$ ,假设有 $x_n$ 它多大程度上是原问题的解，都是问号。好，现在我们耍个小把戏，给 $x_n$ 再起个名字叫 $x_{time}$ .

呐，对于一个完全时间无关的定常问题，求 $x\in[0,\infty)$ 使得 $R(x):= 5x^2+8=0$ , 我们产生了一个随“时间”变化的 $x$ 序列，使用了“时间相关”的“非定常”解法。

只不过，在定常流体力学中，我们面对的是这么个问题：
求 $u:=[\rho,\rho u, \rho v, \rho w, E]^T \in R^5$ 满足 $R(u):=\nabla\cdot F(u) = 0$ + 边界条件。看起来挺像的吧。
PS：算了不展开写了，知乎不支持多行公式，你用MathJax啊@黄继新。

定常问题为什么要用非定常的方法解答？这个命名只不过是一种比拟，因为流体力学方程刚好有定常非定常两个版本。定常问题的时间推进法也叫伪时间推进（pseudo time marching），徒有虚名而已。

到此为止，迫使我们使用时间推进的就是 $R$ 非线性的这个条件，而至于 $R$ 是凸的凹的椭圆的双曲的亚音速的超音速的，根本没机会露脸。至于说时间推进怎么怎么好处的，好像你真的有的选一样！

编辑于 2015-03-08 添加评论感谢分享收藏 • 没有帮助 •

毛颖博，业余PhD

收起

苏襄、星空、傻布等人赞同

我看了所有回答，各有道理，最高票回答最靠谱，本来应该点个赞（我也点了赞）了事，但是我还是好想回答这个问题，毕竟我写了这么久的code。

我先放结论：因为当引入非定常项后，定常方程的类别由可能的Elliptical、Parabolic以及Hyperbolic统一变为Hyperbolic。一旦方程系统变为Hyperbolic，那么方程系统都可以统一使用Upwind 离散方式，而不用根据不同方程的类型对不同变量使用不同的离散方式，这大大提高了一套Code的应用范围。最好的例子就是Fluent，清一色的Upwind Scheme。

月底deadline，等我忙完这阵回来补齐。

---------------我就喜欢拖更新-------------