量子Hall效应与拓扑绝缘体理论(I)
I.分数量子Hall效应
Laughlin波函数与准粒子激发
1982年,崔崎,Stormer和Gossard等人发现了分数量子霍尔效应, 第二 年,Laughlin就给出了一个理论解释。他讨论了一个二维电子气体模型,指出当Landau能级的填充因子偏离基态能量本征值时,系统状态可以由某种元激发来描写,这些元激发具有分数电荷.Halperin在随后发表的一篇文章中指出,Laughlin理论中的元激发准粒子就是服从分数统计的任意子。在Laughlin和Halperin的开创性工作之后, 还有其它很多人探讨了用等效场理论解释分数量子霍尔效应的可能性,在这些工作中,张守晟,Hansson和Kivelson的工作具有相当的重要性。张守晟从微观哈密顿量出发,导出了Chern-Simons-Landau-Ginsberg(CSLG)理论,这一理论所采用的思路和方法都与Laughlin理论相差很大,但它们之间是完全等价的(对此在本文后面会详细阐述)。对于C-S 场这种有效场的演生的物理意义诠释,最早就是 Zhang, Hansson和Kivelson 著名的工作。这种形式的拉格朗日量,作为平均场论,是规范不变的,且能给出二维Laughlin液体态系统中的守恒电流的简单形式,然后引入了一个可以产生这种关系的 规范场。 另一方面在Lopez和Fradkin的工作(费米子场理论)中通过在哈密顿量中引入CS场,相当于将一个磁通捆绑在电子上,这个哈密顿量所描述的电子附带磁通的准粒子,就是复合费米子。
规范场。 另一方面在Lopez和Fradkin的工作(费米子场理论)中通过在哈密顿量中引入CS场,相当于将一个磁通捆绑在电子上,这个哈密顿量所描述的电子附带磁通的准粒子,就是复合费米子。
Laughlin在讨论FQH时候按照IQHE那样忽视了电子间的相互作用,而FQH中能级只是部分地被填充,这时按此道理系统存在无能隙因此无法解释如何形成分数Hall电导平台。

这原因在于量子力学"单粒子"的描写中,零级近似下基态便接近于无限简并,真正的(不简并的)某态必须在计入电子间的长程库仑相互作用消除简并后才能确定。这一理论推测的实验根据是推测的实验根据是:FQHE只能在更低的温度和非常纯净的材料中才能被观察到。另一有关的事实是当填充因子 很小(
很小( )时,理论和实验都证明,电子会排成Wigner晶格。
)时,理论和实验都证明,电子会排成Wigner晶格。
理论上考虑哈密顿量时候可略去动能,写为
而对于多体系统( )此问题根本无法解析求解。于是Laughlin从电子填充最低低(
)此问题根本无法解析求解。于是Laughlin从电子填充最低低( )Landau能级的一个百分比
)Landau能级的一个百分比 出发,并考虑它们之间的库仑相互作用,使基态不可能有无能隙的激发。这也就是说,要考虑N个电子的多体波函数,使之满足Fermi统计,而同时再计入电子间的强关联。从对称规范解得在
出发,并考虑它们之间的库仑相互作用,使基态不可能有无能隙的激发。这也就是说,要考虑N个电子的多体波函数,使之满足Fermi统计,而同时再计入电子间的强关联。从对称规范解得在 的Landau能级中的各个态可以
的Landau能级中的各个态可以  (
( 是Landau能级的简并度;
是Landau能级的简并度; 是电子的复坐标 )分别乘上
是电子的复坐标 )分别乘上  来表示。Laughlin据提出了一个非常简单而含义深刻的尝试波函数
来表示。Laughlin据提出了一个非常简单而含义深刻的尝试波函数 :
:

故Pauli原理要求 间的交换应该使
间的交换应该使 改变符号,即m必须是一个奇数。注意这里m是固定的,故Laughlin波函数不含有任何变分参数,但它竟取得了极大的成功。事实上,它是严格解的最佳近似。
改变符号,即m必须是一个奇数。注意这里m是固定的,故Laughlin波函数不含有任何变分参数,但它竟取得了极大的成功。事实上,它是严格解的最佳近似。
玻色化与CSGL理论
我们需要考察磁场中二维强关联电子气体的FQHE。 处于强磁场下在三维空间运动的电子还填不满第一Landau能级时( ),它们是自旋完全极化的费米子(相反方向极化的能态因巨大的Zeeman劈裂超过Landau能级的问距而可略去不计)。前面提到张首晟引入Chern-Simons规范场后把相互作用的电子气映照成为自由玻色子气(玻色化:bosonization)。
),它们是自旋完全极化的费米子(相反方向极化的能态因巨大的Zeeman劈裂超过Landau能级的问距而可略去不计)。前面提到张首晟引入Chern-Simons规范场后把相互作用的电子气映照成为自由玻色子气(玻色化:bosonization)。
单粒子在电磁场中的作用:

于是带有二维Coulomb相互作用势 多体系统的哈密顿量为
多体系统的哈密顿量为

其本征值问题为:
通过一个幺正变换 将系统的反对称多体波函数映射到对称波函数:
将系统的反对称多体波函数映射到对称波函数:  ;其中
;其中 为
为 粒子间角度
粒子间角度

当 和
和 处电子交换会使得变换
处电子交换会使得变换 得到一个相位移动
得到一个相位移动 故有
故有 。因此为了满足费米子多体系统的反对称统计规律,可令
。因此为了满足费米子多体系统的反对称统计规律,可令  ,那么
,那么 就是对称的玻色场(bosonization)。 现在将哈密顿量
就是对称的玻色场(bosonization)。 现在将哈密顿量 映射为
映射为 ,
,

这里多出一个统计规范项: ,
, 实际上是一种虚拟场。
实际上是一种虚拟场。

二次量子化后得到

其中 为电荷密度算符,在规范条件下
为电荷密度算符,在规范条件下 下统计规范场为
下统计规范场为

其中Levy-Civita符号为 ;流连续性方程为
;流连续性方程为


现在从路径积分出发构造有效场作用量,场量从q数变为c数。玻色场的拉格朗日密度写为 ,就得到路径积分
,就得到路径积分

接着我们需要对整个FQH系统进行路径积分,这时就包括了对统计规范场 的积分。
的积分。
统计规范场的二维Maxwell方程为 ,
, ;实际上,上面二分量统计规范场
;实际上,上面二分量统计规范场 表达式正是在Coulomb规范下的2+1维的Biot-Savart定律。
表达式正是在Coulomb规范下的2+1维的Biot-Savart定律。
进一步对 场引入一个类似时间分量
场引入一个类似时间分量  ,使得拉格朗日量对此分量是线性的。也就是说对此分量积分得到
,使得拉格朗日量对此分量是线性的。也就是说对此分量积分得到 函数(连续归一):
函数(连续归一):

这个 函数约束条件就自动产生
函数约束条件就自动产生  的第一组运动方程,第二组来源于对规范场路径积分的对规范场路径
的第一组运动方程,第二组来源于对规范场路径积分的对规范场路径 取固定规范约束
取固定规范约束 ;这时整体的拉格朗日量为
;这时整体的拉格朗日量为

路径积分合写为

为了对规范场作路径积分,固定规范外,还需在拉格朗日量中引入Fadeev-Popov鬼项 ;重新整理后得到标注准的Chern-Simons拉格朗日量
;重新整理后得到标注准的Chern-Simons拉格朗日量

 ,
,
电子与CS场最小耦合的拉格朗日量(2维QED)

展开也就是以下形式

引入Landau-Ginzburg半经典理论。由于系统具有整体 对称性,因此类似于超流体,玻色场的能谱含有无能隙激发态,也即Goldstone玻色子。玻色场如同玻色超流态那样分解为有质量的振幅场和无质量的相位场:
对称性,因此类似于超流体,玻色场的能谱含有无能隙激发态,也即Goldstone玻色子。玻色场如同玻色超流态那样分解为有质量的振幅场和无质量的相位场: ;对于低能激发情况,长程相互作用按Landau-Ginzburg理论那样以序参量
;对于低能激发情况,长程相互作用按Landau-Ginzburg理论那样以序参量 展开取到四阶项:
展开取到四阶项:

玻色场在整个系统的平均密度处凝聚
用Hubbard-Stratonovich变换积掉高次场量作用项就可以得到有效作用量,这得到了准粒子在平均场中运动的图像。
平均场论在路径积分中意味着近似用经典路径贡献代替所有路径的积分。现在考虑 (无外电场)以及
(无外电场)以及  (均匀磁场,可令其为
(均匀磁场,可令其为  ),在经典
),在经典 场以及
场以及 场方程下,由平均场近似假设可得(注意超流态Goldstone模必须在无规范场时才存在,因此
场方程下,由平均场近似假设可得(注意超流态Goldstone模必须在无规范场时才存在,因此 ):
):
 ,
, ,
,
加上电场 ,根据Noether定理可求出相应的流:
,根据Noether定理可求出相应的流:
 ,
, 
由于在平均场理论中,场量取值是经典路径的期望值,可用 代替
代替 ;在稳场条件下
;在稳场条件下 ,可得到
,可得到
由CS拉格朗日量: ,最终得到
,最终得到
 ,
,
Hall电导为 ,
, ;此时我们可以很直接定义填充因子
;此时我们可以很直接定义填充因子 。
。
从以上半唯象平均场论我们可大致解释分数化Hall电导,为了更细致地研究系统响应性质以及其准粒子激发图像,我们需要更仔细地对路径积分配分函数计算。令所有规范场合成一个有效规范场量记为 ,积掉玻色场:
,积掉玻色场:

这时路径积分描述的是玻色场 对外场
对外场 的响应,在平均场条件成立下,i.e.
的响应,在平均场条件成立下,i.e.  ,
, , 只有很小部分涨落场保留下来。作Fourier变换到动量-频率空间,据此在线性响应理论中有效拉格朗日量只展开到场量的二阶项:
, 只有很小部分涨落场保留下来。作Fourier变换到动量-频率空间,据此在线性响应理论中有效拉格朗日量只展开到场量的二阶项:

 等是展开时得到的系数(超流响应函数);长波极限下准静态响应参数记为
等是展开时得到的系数(超流响应函数);长波极限下准静态响应参数记为  (压缩率)和
(压缩率)和 (超流密度):
(超流密度):

再将统计规范场积掉后得到关于电磁规范场的配分函数(由于拉格朗日量都是二次型,做Gauss积分即可):



电磁响应关联函数为
长波极限下得到压缩率
可见这种玻色场凝聚响应中(玻色凝聚密度不为零 ),压缩率为零,意味着形成了不可压缩液体。而规范场相应的流以及电导先前已经求得,这里不再重复。
),压缩率为零,意味着形成了不可压缩液体。而规范场相应的流以及电导先前已经求得,这里不再重复。
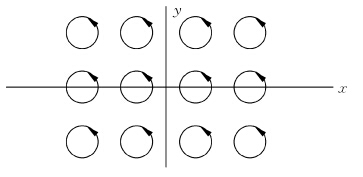
现在以填充因子为 的二维分数量子Hall效应为例说明一下物理图像,这时每个电子平均分到3个
的二维分数量子Hall效应为例说明一下物理图像,这时每个电子平均分到3个  量子磁通.这是指与
量子磁通.这是指与 联系的外磁场。在Chern-Simons有效场论中还有一个C-S规范场
联系的外磁场。在Chern-Simons有效场论中还有一个C-S规范场  ,每个由于每个玻色子带有3个
,每个由于每个玻色子带有3个  的"虚拟磁通"。玻色子与3个
的"虚拟磁通"。玻色子与3个  的虚拟磁通结合后形成的一个个复合体,它们相互交换时因A-B效应而获得一个附加的相位因子使玻色子换位时的对称性转变为反对称性,即复合粒子成为费米子,它是的原来真实电子的低能激发对应物(电性相反的为“准空穴”);也就是说电子在数学上等价于一些带有虚拟的C-S磁通量的"裸玻色子"。因
的虚拟磁通结合后形成的一个个复合体,它们相互交换时因A-B效应而获得一个附加的相位因子使玻色子换位时的对称性转变为反对称性,即复合粒子成为费米子,它是的原来真实电子的低能激发对应物(电性相反的为“准空穴”);也就是说电子在数学上等价于一些带有虚拟的C-S磁通量的"裸玻色子"。因  ,这些"虚拟磁通"方向与外
,这些"虚拟磁通"方向与外 场的磁通的方向相反,彼此抵消的结果使这些玻色子的合磁通为零,即总的结果是FQH系统中的真实电子低能激发成为自由玻色子准粒子。
场的磁通的方向相反,彼此抵消的结果使这些玻色子的合磁通为零,即总的结果是FQH系统中的真实电子低能激发成为自由玻色子准粒子。
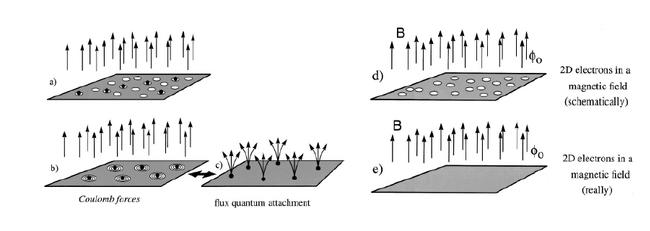
己知无磁场的低温下的玻色子会发送"Bose-Einstein凝聚"(BEC),从而产生超导性(即带电的超流性)。由此也可以解释强关联电子体系的不可压缩性。因为任何电子密度的局域改变,必然引起相伴随的 场磁通的变化,使原来被抵消了的外磁场又再出现来而导致整个系统能量增大(填充因子产生改变)。而超导的Meissner效应告诉我们,超导体内是排斥(弱)磁场的(太强的磁场会破坏超导),所以现在电子体系的密度必须保持均匀不变,因此超导系统中的Cooper对形成的BEC也是不可压缩量子液体。
场磁通的变化,使原来被抵消了的外磁场又再出现来而导致整个系统能量增大(填充因子产生改变)。而超导的Meissner效应告诉我们,超导体内是排斥(弱)磁场的(太强的磁场会破坏超导),所以现在电子体系的密度必须保持均匀不变,因此超导系统中的Cooper对形成的BEC也是不可压缩量子液体。
规范场的有效作用量以及响应性质了解了后,我们还需要了解这种玻色场的响应性质。这次反过来,在路径积分中积掉规范场部分,代入超流玻色场 并略去高阶导数项后得到近似玻色场拉格朗日量:
并略去高阶导数项后得到近似玻色场拉格朗日量:

在动量-频率空间中将振幅场分量积掉后可得到纯粹的相位场有效作用量:


这时可得到
前已经构造出 ,在Coulomb规范中重新积掉
,在Coulomb规范中重新积掉 得
得 关系,在动量-频率空间中为
关系,在动量-频率空间中为 
这时玻色场的有效拉格朗日量为(低能长波极限下略去三体相互作用项):


其中 为顺磁流。不考虑玻色场的涡旋激发(具有非零能量)的各向异性贡献,则顺磁流是纵向的即垂直于相位
为顺磁流。不考虑玻色场的涡旋激发(具有非零能量)的各向异性贡献,则顺磁流是纵向的即垂直于相位  ,流与动量同向,因此拉格朗日量中第三项为零(
,流与动量同向,因此拉格朗日量中第三项为零( )。令
)。令 (均匀不可压缩玻色液体的硬核近似),最后一项在实空间中可表达为:
(均匀不可压缩玻色液体的硬核近似),最后一项在实空间中可表达为:

于是可以看到除了原来的 作用项外,还有一个对数作用项(
作用项外,还有一个对数作用项( )
)

它是由统计规范场形成的,可证明它满足如下二维Poisson方程

有效势 的物理图像是经典电动力学中电子自电势能以及与其他电子之间的Coulomb相互作用能,另外还存在一个均匀的正电荷本底背景,其面密度正比于
的物理图像是经典电动力学中电子自电势能以及与其他电子之间的Coulomb相互作用能,另外还存在一个均匀的正电荷本底背景,其面密度正比于 ;由此可见这幅有效图景正是描述一个经典的电中性二维等离子体。
;由此可见这幅有效图景正是描述一个经典的电中性二维等离子体。
我们知道超流体、超导体是具有非对角长程序的系统,在FQH这种同样发生玻色场凝聚的二维系统中是否也会出现长程序?我们同样通过计算关联函数来揭这一点。再次回到动量-频率空间,有效拉格朗日量经过上述步骤处理后已经变得十分简化,再将玻色场分离为振幅相位场代入可得:

积掉振幅场 后得到相位场
后得到相位场 的有效拉格朗日量
的有效拉格朗日量

因此二次型拉格朗日量中的Green函数为

能谱 ,磁旋频率
,磁旋频率 .
.
静态关联函数为
换到实空间中为

正因为有效玻色场拉格朗日量中出现对数型长程相互作用,从而使得非对角长程序在二维玻色凝聚系统中出现。
通过拉格朗日量可定义正则动量 ,Legendre变换后哈密顿量算符为:
,Legendre变换后哈密顿量算符为:

正则量子化手续下引入对易子: ,在正则动量表象下算符
,在正则动量表象下算符 是对角化的,正则坐标
是对角化的,正则坐标  可由对波函数
可由对波函数 的泛函导数表达:
的泛函导数表达: .因此在此表象下的基态波函数:
.因此在此表象下的基态波函数:

可代入Schrödinger方程 检验,得到本征值
检验,得到本征值  。而其实
。而其实 就是玻色场的振幅自由度
就是玻色场的振幅自由度 (密度涨落),因为其正则共轭量正是相位场。展开玻色场为
(密度涨落),因为其正则共轭量正是相位场。展开玻色场为 ,代入对易关系
,代入对易关系  换到动量空间即可得到
换到动量空间即可得到  ;
; 用
用 代入波函数中得到
代入波函数中得到

这就是所谓Laughlin波函数。
Laughlin波函数与准粒子激发
1982年,崔崎,Stormer和Gossard等人发现了分数量子霍尔效应, 第二 年,Laughlin就给出了一个理论解释。他讨论了一个二维电子气体模型,指出当Landau能级的填充因子偏离基态能量本征值时,系统状态可以由某种元激发来描写,这些元激发具有分数电荷.Halperin在随后发表的一篇文章中指出,Laughlin理论中的元激发准粒子就是服从分数统计的任意子。在Laughlin和Halperin的开创性工作之后, 还有其它很多人探讨了用等效场理论解释分数量子霍尔效应的可能性,在这些工作中,张守晟,Hansson和Kivelson的工作具有相当的重要性。张守晟从微观哈密顿量出发,导出了Chern-Simons-Landau-Ginsberg(CSLG)理论,这一理论所采用的思路和方法都与Laughlin理论相差很大,但它们之间是完全等价的(对此在本文后面会详细阐述)。对于C-S 场这种有效场的演生的物理意义诠释,最早就是 Zhang, Hansson和Kivelson 著名的工作。这种形式的拉格朗日量,作为平均场论,是规范不变的,且能给出二维Laughlin液体态系统中的守恒电流的简单形式,然后引入了一个可以产生这种关系的
Laughlin在讨论FQH时候按照IQHE那样忽视了电子间的相互作用,而FQH中能级只是部分地被填充,这时按此道理系统存在无能隙因此无法解释如何形成分数Hall电导平台。

这原因在于量子力学"单粒子"的描写中,零级近似下基态便接近于无限简并,真正的(不简并的)某态必须在计入电子间的长程库仑相互作用消除简并后才能确定。这一理论推测的实验根据是推测的实验根据是:FQHE只能在更低的温度和非常纯净的材料中才能被观察到。另一有关的事实是当填充因子

理论上考虑哈密顿量时候可略去动能,写为
而对于多体系统(
故Pauli原理要求
玻色化与CSGL理论
我们需要考察磁场中二维强关联电子气体的FQHE。 处于强磁场下在三维空间运动的电子还填不满第一Landau能级时(
单粒子在电磁场中的作用:
于是带有二维Coulomb相互作用势
其本征值问题为:
通过一个幺正变换
当
这里多出一个统计规范项:
二次量子化后得到
其中
其中Levy-Civita符号为
现在从路径积分出发构造有效场作用量,场量从q数变为c数。玻色场的拉格朗日密度写为
接着我们需要对整个FQH系统进行路径积分,这时就包括了对统计规范场
统计规范场的二维Maxwell方程为
进一步对
这个
路径积分合写为
为了对规范场作路径积分,固定规范外,还需在拉格朗日量中引入Fadeev-Popov鬼项
电子与CS场最小耦合的拉格朗日量(2维QED)
展开也就是以下形式
引入Landau-Ginzburg半经典理论。由于系统具有整体
玻色场在整个系统的平均密度处凝聚
用Hubbard-Stratonovich变换积掉高次场量作用项就可以得到有效作用量,这得到了准粒子在平均场中运动的图像。
平均场论在路径积分中意味着近似用经典路径贡献代替所有路径的积分。现在考虑
加上电场
由于在平均场理论中,场量取值是经典路径的期望值,可用
由CS拉格朗日量:
Hall电导为
从以上半唯象平均场论我们可大致解释分数化Hall电导,为了更细致地研究系统响应性质以及其准粒子激发图像,我们需要更仔细地对路径积分配分函数计算。令所有规范场合成一个有效规范场量记为
这时路径积分描述的是玻色场
再将统计规范场积掉后得到关于电磁规范场的配分函数(由于拉格朗日量都是二次型,做Gauss积分即可):
电磁响应关联函数为
长波极限下得到压缩率
可见这种玻色场凝聚响应中(玻色凝聚密度不为零
现在以填充因子为

己知无磁场的低温下的玻色子会发送"Bose-Einstein凝聚"(BEC),从而产生超导性(即带电的超流性)。由此也可以解释强关联电子体系的不可压缩性。因为任何电子密度的局域改变,必然引起相伴随的
规范场的有效作用量以及响应性质了解了后,我们还需要了解这种玻色场的响应性质。这次反过来,在路径积分中积掉规范场部分,代入超流玻色场
在动量-频率空间中将振幅场分量积掉后可得到纯粹的相位场有效作用量:
这时可得到
前已经构造出
这时玻色场的有效拉格朗日量为(低能长波极限下略去三体相互作用项):
其中
于是可以看到除了原来的
它是由统计规范场形成的,可证明它满足如下二维Poisson方程
有效势
我们知道超流体、超导体是具有非对角长程序的系统,在FQH这种同样发生玻色场凝聚的二维系统中是否也会出现长程序?我们同样通过计算关联函数来揭这一点。再次回到动量-频率空间,有效拉格朗日量经过上述步骤处理后已经变得十分简化,再将玻色场分离为振幅相位场代入可得:
积掉振幅场
因此二次型拉格朗日量中的Green函数为
能谱
静态关联函数为
换到实空间中为
正因为有效玻色场拉格朗日量中出现对数型长程相互作用,从而使得非对角长程序在二维玻色凝聚系统中出现。
通过拉格朗日量可定义正则动量
正则量子化手续下引入对易子:
可代入Schrödinger方程
这就是所谓Laughlin波函数。
本文由Phantom_Ghost授权(果壳网)发表,文章著作权为原作者所有。
No comments:
Post a Comment