Chern-Simons理论中的统计规范场没有独立的动力学自由度,因而并不描写有独立动力学的粒子,它的唯一作用在于给出分数统计所要求的额外相因子。
量子Hall效应与拓扑绝缘体理论(III)
交换统计
单从形式上看是多体波函数的形式构造 ,m是奇数是源于电子的交换反对称性,且是填充数倒数。正是Laughlin抓住了FQH系统的元激发的分数统计性质,才使得他的理论大获成功。实际上这种形式也正是决定了其分数统计性质;我们可以反过来看待,若先不考虑具体的Laughlin波函数形式,从二维的分数统计出来看,Laughlin波函数的形式是必然的。我们考察的量子多体系统的交换统计。在全同粒子系统中,交换两个粒子坐标的操作用置换群描写。置换群包含 两个元素,单位算子 (即不做变换)和置换算子
(即不做变换)和置换算子 。将置换算子
。将置换算子 作用在系统波函数上。由于
作用在系统波函数上。由于 ,可知置换算子的本征值为
,可知置换算子的本征值为 ,其对应的本征函数分别是对称的和反对称的,而相应的粒子分别是玻色子和费米子。 我们知道QHE多体系统中的低能激发产生的准粒子是任意子,带着个虚拟磁通,而任意子交换过程中而磁通会贡献相位的,而交换粒子的这个相位将决定统计性质,那么统计关系就会不一样:电子1的规范势是和电子2相关联的,可以类比为,电子1绕电子2转一圈就像绕着一个虚拟磁通转了一圈,那么1跟2电子的整体波函数就会多出一个与磁通相关的不可积相位,磁通决定着相位因子若取不同的值在统计上会有不一样的效果。
,其对应的本征函数分别是对称的和反对称的,而相应的粒子分别是玻色子和费米子。 我们知道QHE多体系统中的低能激发产生的准粒子是任意子,带着个虚拟磁通,而任意子交换过程中而磁通会贡献相位的,而交换粒子的这个相位将决定统计性质,那么统计关系就会不一样:电子1的规范势是和电子2相关联的,可以类比为,电子1绕电子2转一圈就像绕着一个虚拟磁通转了一圈,那么1跟2电子的整体波函数就会多出一个与磁通相关的不可积相位,磁通决定着相位因子若取不同的值在统计上会有不一样的效果。
整数量子统计:
分数量子统计:
在一般的量子统计中,我们从不考虑粒子交换的路径会对统计性质有什么影响。因为在三维空间,两个粒子无论以什么方式互相绕一圈,形成任意的闭合曲线,这条闭合曲线总可以连续收缩为一点,它们都是拓扑等价的,或说所有闭合曲线属于同一拓扑等价类。路径的不同不会对置换群的表示有任何影响。但在二维平面(空间),情况则截然不同。 考虑平面上的一条闭合曲线,该平面上它包围区域里有一个奇点。如果在三维空间中,这条曲线可以绕过奇点而收缩为一点,但如果在二维平面里,那么这条曲线在收缩过程中就不可避免地碰到这个点,从而永远无法收缩为一点。这 就造成了二维平面中置换两个粒子坐标时粒子所走过的路径并不属于同一等价类。因此必须对路径进行分类,这样一来置换群的概念也要推广以区分不同等价类的路径。
描述这一问题的标准数学语言是同伦群。同伦群的精确定义比较抽象,我们这里用一个简单的例子来说明。考虑二维平面,由于绕一个点N圈的所有闭合曲线都是拓扑等价的,可以把绕点N周的所有闭合曲线组成的等价类作为同伦群的一个元素,很容易验证它们满足群的定义。这个群叫一阶同伦群,也称为基本群。 N个全同粒子系统的二维位形空间非常复杂,这个位形空间的同伦群是个无限群。位形空间分成若干不相连的区域,路径分成不相连的分支,每个分支作为一个元素组成所谓的辫子群。直观地说,两个全同粒子在二维平面中运动,它们划过的世界线相互缠绕,编成一条辫子,编辫子的不同方式就构成辫子群的元素。与此对应,任意子系统的波函数的Hilbert空间不再是置换群的表示,而是辫子群的表示,也就是说,在二维平面里只用置换群对路径分类是不够的,必须用辫子群做进一步的考查。

现在以微分几何的角度来更细致地描述分数统计的数学结构。Hilbert空间中的波函数 犹如普通向量空间中一个矢量
犹如普通向量空间中一个矢量 的分量
的分量 ,因为
,因为 ,
, 是基矢。
是基矢。 维的位形空间是纤维丛
维的位形空间是纤维丛 的一个底流形
的一个底流形 ,在
,在 的每一点
的每一点 上有一根一维的纤维
上有一根一维的纤维 ,它是单分量的Hilbert空间
,它是单分量的Hilbert空间 。局部地看总有
。局部地看总有 ,因此有时宽泛地把波函数
,因此有时宽泛地把波函数 说成是纤维丛的截面,因为它是一个复函数,定义在底流形每一点的纤维上。但是实际上,比如说,对于一个切矢量丛
说成是纤维丛的截面,因为它是一个复函数,定义在底流形每一点的纤维上。但是实际上,比如说,对于一个切矢量丛 ,纤维是切平面,而截面是矢量场
,纤维是切平面,而截面是矢量场 ,它给出一个映照
,它给出一个映照 ,或
,或 。因为
。因为

见对应关系是 。所以
。所以 是截面的整体的抽象表示,而
是截面的整体的抽象表示,而 则是截面的局域的具体表示。
则是截面的局域的具体表示。 在不依赖于某基矢
在不依赖于某基矢 的局域性质这一点上来说是惟一的和普适的,但
的局域性质这一点上来说是惟一的和普适的,但 依赖于
依赖于 ,就不能说是惟一的和普适的。不过通常量子力学系统会对波函数提出诸如单值性的要求,这是因为当某流形
,就不能说是惟一的和普适的。不过通常量子力学系统会对波函数提出诸如单值性的要求,这是因为当某流形 的拓扑性质是可缩的(con-tractible)时候,在它上面构造的纤维丛总是平庸的:我们总可以通过平移在整个流形上定义基矢
的拓扑性质是可缩的(con-tractible)时候,在它上面构造的纤维丛总是平庸的:我们总可以通过平移在整个流形上定义基矢 而在每一点得到惟一的结果,即总有
而在每一点得到惟一的结果,即总有 。
。
当然,在考虑一般的切丛时候,纤维的截面是矢量场,因此态矢才是截面整体抽象表示不依赖于坐标基矢,波函数只能说是截面的局域依赖于基矢表示。 不过我们要讨论二维( )平面有许多全同粒子的情形,存在多值波函数,这时候就不那么简单就认为波函数就和态矢一一对应了。那这时就要通过收缩约化底流形来讨论,就是接下来要讲的内容。
)平面有许多全同粒子的情形,存在多值波函数,这时候就不那么简单就认为波函数就和态矢一一对应了。那这时就要通过收缩约化底流形来讨论,就是接下来要讲的内容。
考虑在 的欧氏空间
的欧氏空间 上有n个全同粒子在运动。物理组态空间并不简单地就是
上有n个全同粒子在运动。物理组态空间并不简单地就是 .首先,任何两个粒子的位置重合是不允许的,因此底流形从
.首先,任何两个粒子的位置重合是不允许的,因此底流形从 收缩到
收缩到 ,
, 表示
表示 中的对角点,即
中的对角点,即 而其中对某个
而其中对某个 有
有 。其次,即使在经典水平上也必须计入全同粒子的不可区别性,于是底流形进一步由
。其次,即使在经典水平上也必须计入全同粒子的不可区别性,于是底流形进一步由 缩到
缩到 三一,表不任何两个组态若能通过粒子间的一个置换群
三一,表不任何两个组态若能通过粒子间的一个置换群 联系起来时将被认为是等同的。考虑
联系起来时将被认为是等同的。考虑 的情形:因为质心继标
的情形:因为质心继标 二是平庸的,只需要研究相对半标
二是平庸的,只需要研究相对半标 。在平面
。在平面 上,原点
上,原点 (对应于
(对应于 )必须作为一个奇点被除去。从原点沿一直线把此平面剪开,然后把它折成一个半角为
)必须作为一个奇点被除去。从原点沿一直线把此平面剪开,然后把它折成一个半角为 的圆锥,如果将此具有两叶的圆锥面在剖线处交叉地连接两叶,使得到
的圆锥,如果将此具有两叶的圆锥面在剖线处交叉地连接两叶,使得到 流形;若将上下两叶等同起来,便得到
流形;若将上下两叶等同起来,便得到 ,它正是在
,它正是在 上两个全同粒子的正确的物理组态空间。在
上两个全同粒子的正确的物理组态空间。在 上粒子坐标
上粒子坐标 和
和 可通过反钟向
可通过反钟向 的旋转而交换(见下图,相当于在
的旋转而交换(见下图,相当于在 上绕锥顶的一个逆时针方向闭曲线
上绕锥顶的一个逆时针方向闭曲线 ;若位置的交换
;若位置的交换 通过
通过 上一顺时针方向的
上一顺时针方向的 转动而实现,它便相当于
转动而实现,它便相当于 上一顺钟向的闭曲线
上一顺钟向的闭曲线 。由于M2上存在奇点
。由于M2上存在奇点 ,
, 和
和 既不能通过连续变形互变,也不能缩成一点.事实上,
既不能通过连续变形互变,也不能缩成一点.事实上, ,
, 还有
还有 (它可以连续变形收缩为一点)是一阶同伦群
(它可以连续变形收缩为一点)是一阶同伦群 的3个基本生成元。
的3个基本生成元。
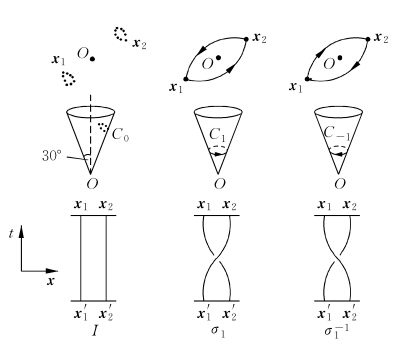
 上的
上的 和
和 ,它们又分别对应于图中的
,它们又分别对应于图中的 和
和 。一般地,
。一般地, 的一维幺正表示为:
的一维幺正表示为:
这里 是模型的参数,
是模型的参数, 称为缠绕数。借助前面引入的Hilbert丛的概念,首先定义记号:在
称为缠绕数。借助前面引入的Hilbert丛的概念,首先定义记号:在 上的某一个位置某矢记为
上的某一个位置某矢记为 ,它表示第一个粒子在位置
,它表示第一个粒子在位置 而第二个粒子在位置
而第二个粒子在位置 ,
, 。另一方面,在
。另一方面,在 上的一个位置某矢记为
上的一个位置某矢记为 ,它表示有一个粒子位于
,它表示有一个粒子位于 而另一个位于
而另一个位于 。考虑在Hilbert空间两全同粒子的一个态矢
。考虑在Hilbert空间两全同粒子的一个态矢 ,我们可以在整体上定义一个单值的截面,它取值在流形
,我们可以在整体上定义一个单值的截面,它取值在流形 上的一根纤维上:
上的一根纤维上:

展开写为:


这里定义两类基矢之间的转换函数为:

 对应于辫子群中的单位元
对应于辫子群中的单位元
 是定义在基
是定义在基  上定义的多值波函数。
上定义的多值波函数。
进一步的位置交换 ,
, 变为
变为 ,它已经包含在前面
,它已经包含在前面 的求和式表达式之中。
的求和式表达式之中。 的多值性可以在图上看出:那里引入虚拟的时间
的多值性可以在图上看出:那里引入虚拟的时间 并用
并用 来表示两根弦相互缠绕数,从下面但标
来表示两根弦相互缠绕数,从下面但标 出发的弦不妨对应于第
出发的弦不妨对应于第 个粒子的"轨迹",故
个粒子的"轨迹",故 对应于
对应于 流形上的坐标。另一方面,坐标
流形上的坐标。另一方面,坐标 应当理解为在
应当理解为在 上位置的标记,因此不是对特定的粒子标记而是对位形坐标
上位置的标记,因此不是对特定的粒子标记而是对位形坐标 与
与 ,其交换为对称的。
,其交换为对称的。
在流形 中引入联络,由平移不变条件:
中引入联络,由平移不变条件:

引入一个联络 ,其部分决定于系统的动力学,部分决定于规范选择。由此可从
,其部分决定于系统的动力学,部分决定于规范选择。由此可从 出发得到所有
出发得到所有  , 类比构造几何相位的方法,即像典型的A-B相位那样对规范势(联络)绕圈作积分:
, 类比构造几何相位的方法,即像典型的A-B相位那样对规范势(联络)绕圈作积分:

这样也就给出与辫子群同构的和乐群(给出一阶同伦群到规范群 的映射,其本身也是辫子群的幺正一维表示,对于闭合路径
的映射,其本身也是辫子群的幺正一维表示,对于闭合路径 ,积分应该得到
,积分应该得到  ,并且在无外场时自然要求流形的曲率张量为零。为了得到这样的联络,使用平凡的Abelian联络——Kohno联络1形式:
,并且在无外场时自然要求流形的曲率张量为零。为了得到这样的联络,使用平凡的Abelian联络——Kohno联络1形式:
 ,
,
鉴于我们只考察多体系统的统计性质,那么联络 便只联系于同伦群
便只联系于同伦群  ,而不考虑外力场时,
,而不考虑外力场时, 的曲率为零:
的曲率为零: ,换言之,除了流形中的奇点,物理组态空间是局域处处平坦的。然而正是那些奇点的存在,使得我们能上面平凡的联络得出非平凡的和乐群元。为了得到和乐群元,我们需要一个非平凡的Abelian Kohno联络:
,换言之,除了流形中的奇点,物理组态空间是局域处处平坦的。然而正是那些奇点的存在,使得我们能上面平凡的联络得出非平凡的和乐群元。为了得到和乐群元,我们需要一个非平凡的Abelian Kohno联络: ,有
,有

由之前提出的联络平移条件得出:


解出 :
:


那么对于 上一个闭合曲线
上一个闭合曲线  ,则有
,则有

波函数 与
与 多值性正好相反保证了截面
多值性正好相反保证了截面 的单值性:
的单值性:

自然得到Laughlin波函数形式

这里 就是底流形收缩约化掉交换后的新的底流形纤维的单值截面;
就是底流形收缩约化掉交换后的新的底流形纤维的单值截面; 是决定着统计性质的参数,称为统计角。
是决定着统计性质的参数,称为统计角。
如果比较Wilzeck的任意子模型的哈密顿量Hamiltonian和Chern-Simons场的作用量,会发现二者速途同归:前者是构造荷电带虚拟磁通的任意子,后者是荷电玻色子与Chern-Simons场耦合的结果。引入了C-S 场后,和荷电粒子耦合就会出现这种虚拟的磁通(规范势),

由此可见非零场强只定域在粒子世界线上,因此粒子间不存在经典的Lorentz力,这也就是为何称为虚拟规范势的原因。在二维平面上有磁通 过的环形区域内一个带有分数电荷准拉必然带有非定域信息(因为这些准粒子是有效平均场的低能激发,是整体而非局域的),从图中可看到
过的环形区域内一个带有分数电荷准拉必然带有非定域信息(因为这些准粒子是有效平均场的低能激发,是整体而非局域的),从图中可看到 处有一条看不见的"奇异弦"。这样就模拟出Wilzeck的复合粒子(任意子)。
处有一条看不见的"奇异弦"。这样就模拟出Wilzeck的复合粒子(任意子)。

Chern-Simons理论中的统计规范场没有独立的动力学自由度,因而并不描写有独立动力学的粒子,它的唯一作用在于给出分数统计所要求的额外相因子。从场方程可以明显地看出这一点:统计规范场的场量完全由物质流确定,因此它的方程确切地说是一个约束条件。引入Chern-Simons项另一个好处是可以清晰地讨论 、
、 破缺, 这里
破缺, 这里 代表时间反演,
代表时间反演, 代表宇称变换。从数学上可以证明, 具有分数统计性质的任意子体系会破坏空间、时间反演对称性,也就是存在C-S场耦合的系统其基态在
代表宇称变换。从数学上可以证明, 具有分数统计性质的任意子体系会破坏空间、时间反演对称性,也就是存在C-S场耦合的系统其基态在 反演下不对称。 因此,考查
反演下不对称。 因此,考查 或
或 的破缺与否是判断C-S理论是否正确的一个重要检验方法。值得注意的是QCD轴子场论的
的破缺与否是判断C-S理论是否正确的一个重要检验方法。值得注意的是QCD轴子场论的 真空也会破坏
真空也会破坏 、
、 对称性。
对称性。
II.拓扑不变量
QHE与陈数
我们已经知道Chern-Simons项是个拓扑不变量,其本质是第三陈类。那么回过头来我们发现量子霍尔效应的电导率包含的系数正是个第一陈类积分而得的陈数。

在上世纪80年代以前人们对物质状态进行分类的主要依据是体系的对称性。依据传统的相变理论。不同的量子态可以通过Landau自发对称性破缺的原理来理解,对称性由序参量描述对称性破缺意味着序参量不为零的有序相的出现。举例来说,晶体破坏了空间连续平移对称性;铁磁体破坏了空间旋转对称性;超导体破坏 规范对称性。而整数量子Hall效应与分数量子Hall效应的发现打破了传统的Landau相变理论。因为量子Hall态的产生并没有破坏任何对称性(不存在局域序参量),无法纳入Landau自发对称性破缺的理论框架中。因此要理解量子Hall态需要引入拓扑序的概念,相应的,量子Hall态就是一种拓扑相。而Hall电导是整数是量子化的
规范对称性。而整数量子Hall效应与分数量子Hall效应的发现打破了传统的Landau相变理论。因为量子Hall态的产生并没有破坏任何对称性(不存在局域序参量),无法纳入Landau自发对称性破缺的理论框架中。因此要理解量子Hall态需要引入拓扑序的概念,相应的,量子Hall态就是一种拓扑相。而Hall电导是整数是量子化的 对样品的大小形状载流子密度甚至迁移率均不敏感这说明存在某种内在的不变量。我们知道数学上拓扑学是研究拓扑空间中的几何不变量的学问。在凝聚态物理上,拓扑的概念是针对有能隙系统(绝缘体超导体)而言。每个有能隙的多体系统都由相应的哈密顿量来描述,如果两个系统的哈密顿量可以通过连续形变(譬如调节哈密顿量里的参数)而光滑过渡;即形变过程中,不闭合体能隙。从动力学角度而言也就意味着对任何局部微扰都具有鲁棒性而呈现的拓扑保护性,任何的局部微扰指的是
对样品的大小形状载流子密度甚至迁移率均不敏感这说明存在某种内在的不变量。我们知道数学上拓扑学是研究拓扑空间中的几何不变量的学问。在凝聚态物理上,拓扑的概念是针对有能隙系统(绝缘体超导体)而言。每个有能隙的多体系统都由相应的哈密顿量来描述,如果两个系统的哈密顿量可以通过连续形变(譬如调节哈密顿量里的参数)而光滑过渡;即形变过程中,不闭合体能隙。从动力学角度而言也就意味着对任何局部微扰都具有鲁棒性而呈现的拓扑保护性,任何的局部微扰指的是  形式的厄米算符,其中
形式的厄米算符,其中  只作用在有限范围区域(*依据这种定义,拓扑绝缘体并非真正意义上的“拓扑”,因其不具有对任何局部微扰都鲁棒的特性,就例如破坏
只作用在有限范围区域(*依据这种定义,拓扑绝缘体并非真正意义上的“拓扑”,因其不具有对任何局部微扰都鲁棒的特性,就例如破坏  和时间反演对称性的情况;因此对于拓扑绝缘体更合适应称为“
和时间反演对称性的情况;因此对于拓扑绝缘体更合适应称为“  和时间反演对称性保护的绝缘体”,它是对称性保护(SPT)拓扑序系统的一个例子)。那么我们称这两个系统属于同一个拓扑等价类。关闭体能隙伴随着量子相变,体能隙的闭合意味着动量空间中出现奇点,也就是在BZ流形上产生“洞”(亏格不为零)。为了判断两个系统是否属于同一个拓扑等价类须要引入在同胚映射下不变的代数量:拓扑不变量。它可以是一个数(例如欧拉示性数、陈数)。也可以是构建在拓扑空间上的某种代数结构,如同伦群、同调群、上同调群等。具有不同的拓扑有序态的系统必须由不同的拓扑不变量来进行描述。
和时间反演对称性保护的绝缘体”,它是对称性保护(SPT)拓扑序系统的一个例子)。那么我们称这两个系统属于同一个拓扑等价类。关闭体能隙伴随着量子相变,体能隙的闭合意味着动量空间中出现奇点,也就是在BZ流形上产生“洞”(亏格不为零)。为了判断两个系统是否属于同一个拓扑等价类须要引入在同胚映射下不变的代数量:拓扑不变量。它可以是一个数(例如欧拉示性数、陈数)。也可以是构建在拓扑空间上的某种代数结构,如同伦群、同调群、上同调群等。具有不同的拓扑有序态的系统必须由不同的拓扑不变量来进行描述。
在量子Hall效应中,人们研究时候发现其Hall电导系数正是刻画具有不同的拓扑有序态的系统必须由不同的拓扑不变量来进行描述拓扑序的量,具有拓扑不变性,就像某种“几何”内蕴的“示性数”;只不过这里的"几何"是在哈密顿量的赝自旋靶空间或者动量空间中诱导出来的纤维丛(Bloch丛)上(根据主丛的定义,就是 纤维空间与
纤维空间与 底流形的直积结构;可类比于电磁场,所不同的是其底流形是
底流形的直积结构;可类比于电磁场,所不同的是其底流形是  )。
)。

我们知道微分几何中有 “Gauss-Bonnet定理” : 对于一个无边界二维流形 ,定理表明有
,定理表明有  。 这里
。 这里  是Gauss曲率,
是Gauss曲率, 是亏格。 对于环面,
是亏格。 对于环面, 并且积分为零。
并且积分为零。

Gauss-Bonnet定理是讨论的是几何流形的拓扑。而与 有关的是
有关的是 环面流形上的
环面流形上的 纤维丛的拓扑; 或者说这是关于Bloch波函数怎样整体的表现的。真正起作用的是开头就提到的Chern-Weil理论,可以视为Gauss-Bonet定理的推广。 磁场
纤维丛的拓扑; 或者说这是关于Bloch波函数怎样整体的表现的。真正起作用的是开头就提到的Chern-Weil理论,可以视为Gauss-Bonet定理的推广。 磁场  ,或者相当的场强
,或者相当的场强  ,是
,是  流形上
流形上  丛的几何曲率. Chern-Weil理论描述的是对该曲率的积分定义出陈类:
丛的几何曲率. Chern-Weil理论描述的是对该曲率的积分定义出陈类:

它就是 丛上的拓扑不变量(再次类比电磁理论,开头提到电磁场是
丛上的拓扑不变量(再次类比电磁理论,开头提到电磁场是 纤维丛上的联络,而A-B相则是其中的拓扑不变量)。 就像Gauss-Bonnet定理表述的是对Gauss曲率的积分是流形上的拓扑不变量。 因此这种对比也可以让人们对陈数
纤维丛上的联络,而A-B相则是其中的拓扑不变量)。 就像Gauss-Bonnet定理表述的是对Gauss曲率的积分是流形上的拓扑不变量。 因此这种对比也可以让人们对陈数  有更直观的几何理解:
有更直观的几何理解: 实际上是动量空间,经典的微分几何里面的Gauss-Bonnet定理是描述几何的位形空间,其Gauss曲率对应着
实际上是动量空间,经典的微分几何里面的Gauss-Bonnet定理是描述几何的位形空间,其Gauss曲率对应着 曲率。
曲率。

类比于光滑流形,进一步推广到纤维丛 的示性类
的示性类  ,它是定义其底流形
,它是定义其底流形 的上同调类,
的上同调类,  ;示性类在整个底流形上的积分成为示性数,它是与不依赖于联络选择的拓扑不变量。陈类则是针对复向量丛定义的,考虑k维复向量丛
;示性类在整个底流形上的积分成为示性数,它是与不依赖于联络选择的拓扑不变量。陈类则是针对复向量丛定义的,考虑k维复向量丛  ,其结构群
,其结构群  可约化为
可约化为 ,纤维为k维复向量空间
,纤维为k维复向量空间  ,联络
,联络 (物理上为规范场)与曲率
(物理上为规范场)与曲率 (场强张量)都取值于李代数
(场强张量)都取值于李代数 上。取李代数
上。取李代数 的基础表示,则
的基础表示,则 与
与 分别为
分别为 矩阵的1-形式与2-形式,关系为
矩阵的1-形式与2-形式,关系为 
曲率矩阵的不变多项式称为总陈类:

 是偶数维形式,即
是偶数维形式,即  ,称为第 j 陈类。因
,称为第 j 陈类。因  是底流形
是底流形 上的2j 阶闭形式,因此它定义了上同调群
上的2j 阶闭形式,因此它定义了上同调群  的群元:
的群元: ,可以证明
,可以证明




陈类在整个底流形上的积分(复向量丛 第j陈数)为整数:
第j陈数)为整数:

1982 年Thouless等人(TKNN)在一片奠基性文章中利用Kubo公式(线性响应理论)就算了二维周期性晶格系统的Hall电导发现其具有和Berry相一样的数学结构,因而进一步指出 系统自身变化的不敏感性来源于QHE体系的拓扑不变性,他们将该拓扑不变量称为
系统自身变化的不敏感性来源于QHE体系的拓扑不变性,他们将该拓扑不变量称为  数,用整数
数,用整数 表示。其能带的拓扑性与一般绝缘体截然不同,以第一陈类来对定义在复数域上的任意维哈密顿量进行拓扑分类。 QHE态中
表示。其能带的拓扑性与一般绝缘体截然不同,以第一陈类来对定义在复数域上的任意维哈密顿量进行拓扑分类。 QHE态中 为非零的整数对应量子电导前的系数,普通绝缘体n为零,普通绝缘体和真空有相同的拓扑分类。因此整数量子霍尔系统的拓扑不变量就由第一陈数来表征。QHE态和真空拓扑性不同其和真空的界面上拓扑不变量必须发生变化这导致了无能隙导电的边缘态出现。
为非零的整数对应量子电导前的系数,普通绝缘体n为零,普通绝缘体和真空有相同的拓扑分类。因此整数量子霍尔系统的拓扑不变量就由第一陈数来表征。QHE态和真空拓扑性不同其和真空的界面上拓扑不变量必须发生变化这导致了无能隙导电的边缘态出现。

Laughlin在对整数量子Hall效应时候,考虑到系统中的电子波函数整体相位相干性,引入横向周期性边界条件将位形空间构造成环带形状(torus: ),在此从近自由的单电子模型出发在系统的哈密顿量中加上磁场,解二维环带域(计入在相应的长宽两组周期性边界条件)Schrödinger方程,得到能级Landau能级。
),在此从近自由的单电子模型出发在系统的哈密顿量中加上磁场,解二维环带域(计入在相应的长宽两组周期性边界条件)Schrödinger方程,得到能级Landau能级。

实际的样品中,需要考虑存在杂质并束缚电子使之成为定域态,有掺杂的情况,每一Landau能级己扩展为能带(扩展边缘态)。一定范围内磁场变化时候电子落在定域束缚态中使得自由电子数目不增加,从而出现Hall电导平台。

以TKNN(Thouless-Kohmoto-Nightingale-deNijs) 拓扑不变量角度去阐述IQHE则是更现代的凝聚态理论。二维IQHE系统的有效场理论哈密顿量(Haldane模型)为:

解出的能谱中含有无能隙手征边缘态的谱线,其中的手性费米子不能反向散射,因而整数量子Hall系统是破坏时间反演对称的(Haldane哈密顿量中的磁场“质量”项使得零质量手征费米子激发破坏)。边界上的边缘态数量为: ,一般IQHE系统中
,一般IQHE系统中 。
。
*这里要顺带说一下,通俗的整数量子Hall效应的直观解释是这样说:电子在磁场中因为受到总是垂直于电子的运动方向的洛伦兹力,于是就形成一个圈。磁场很强的情况下,电子的轨道半径很小,因此电子都束缚在Landau态中成为束缚态,把所有这些轨道填满了就没地方可以去了(这也就是电子把逐个Landau能级填满)。但是当靠近样品边缘的时候,电子没有办法跑出一整个轨道了,于是只能沿着样品的边缘跳,画出一个接一个的半圆弧。也就是说,电流是可以沿着边缘传导的。而且因为电子只能沿着单一方向转圈,边缘上电流是“单行道”,只能沿一个方向传输,(也即上面所说的“手征边缘态”)。

这种经典解释的图像看起直观,但并真的不是量子力学里面所描述的图像:显然量子力学里面没有什么一个个固定的圆形轨道,我们之前就讨论过Landau能级,再次需要再次提醒大家注意这个才是真正的物理图景。但这个通俗直观的解释也有其精妙的地方:我们知道在量子力学中,动量算符为 ,这个算符作用到波函数上最明显的意义并不是得到动量(经典意义下动量是
,这个算符作用到波函数上最明显的意义并不是得到动量(经典意义下动量是  ),而是计算出了波函数的相位增加的梯度。那么回顾在对称规范条件下得到的一个个在平面上排列成WS晶格的Landau能级(见上面Landau states的图),每个点上的波函数其相位按逆时针方向增长,角动量算符为
),而是计算出了波函数的相位增加的梯度。那么回顾在对称规范条件下得到的一个个在平面上排列成WS晶格的Landau能级(见上面Landau states的图),每个点上的波函数其相位按逆时针方向增长,角动量算符为  。那么在这个意义下,电子也确实可以算是在“转圈圈”
。那么在这个意义下,电子也确实可以算是在“转圈圈”
*对于电子在磁场中的偏转运动的量子层面解释是和相位有关。这里首先不妨考虑Landau规范: ,矢势
,矢势 (就是Berry 联络)有不为零的旋度
(就是Berry 联络)有不为零的旋度 (就是Berry曲率)。现在让荷电粒子沿
(就是Berry曲率)。现在让荷电粒子沿 轴按平面波入射
轴按平面波入射  ,等相面平行于x轴。因为粒子沿矢势平移要积累Berry相位,平移单位距离积累的Berry相位与矢势成正比。而等相面各点的矢势都不同,因此沿
,等相面平行于x轴。因为粒子沿矢势平移要积累Berry相位,平移单位距离积累的Berry相位与矢势成正比。而等相面各点的矢势都不同,因此沿 方向传播一段距离以后,各点积累了不同的相位,等相面就会倾斜。从而等相面一边沿
方向传播一段距离以后,各点积累了不同的相位,等相面就会倾斜。从而等相面一边沿 轴推进一边倾斜,这就表现为荷电粒子的偏转。 如果让粒子沿着x轴入射, 此时等相面上积累的相位是相同的,波前不会“倾斜”,我们知道粒子依旧偏转。而这仍然可以从波函数解释。 在分析之前首先严格清晰地区分好三种不同的动量,
轴推进一边倾斜,这就表现为荷电粒子的偏转。 如果让粒子沿着x轴入射, 此时等相面上积累的相位是相同的,波前不会“倾斜”,我们知道粒子依旧偏转。而这仍然可以从波函数解释。 在分析之前首先严格清晰地区分好三种不同的动量, 是正则动量,规范联络 A是电磁动量,质量乘速度
是正则动量,规范联络 A是电磁动量,质量乘速度  是机械动量,它们三者的关系是
是机械动量,它们三者的关系是  。直接与波函数的相位变化相联系的是正则动量(这是显而易见的),波函数的相位不存在梯度那么正则动量为零,但这并不意味着粒子没有偏转。这是因为在有磁场存在的情况下,不能简单地从波函数的等相面来分析粒子运动的方向。波函数等相面的法线方向(就是相位梯度的方向)是正则动量的方向(因为正则动量算符就是梯度算符),但是正则动量的方向未必是粒子运动的方向。直观的粒子运动的方向是机械动量决定的,而机械动量需要在正则动量的基础上扣除电磁动量得到。这个扣除电磁动量的过程对于波函数来说就是通过对波函数进行规范变换来消除等相面上的规范联络(Peierls substitution)。如上面提到的例子,粒子沿
。直接与波函数的相位变化相联系的是正则动量(这是显而易见的),波函数的相位不存在梯度那么正则动量为零,但这并不意味着粒子没有偏转。这是因为在有磁场存在的情况下,不能简单地从波函数的等相面来分析粒子运动的方向。波函数等相面的法线方向(就是相位梯度的方向)是正则动量的方向(因为正则动量算符就是梯度算符),但是正则动量的方向未必是粒子运动的方向。直观的粒子运动的方向是机械动量决定的,而机械动量需要在正则动量的基础上扣除电磁动量得到。这个扣除电磁动量的过程对于波函数来说就是通过对波函数进行规范变换来消除等相面上的规范联络(Peierls substitution)。如上面提到的例子,粒子沿 轴入射,等相面平行于
轴入射,等相面平行于 轴,虽然等相面没有偏转,但是粒子实际上却是偏转了。 在等相面上,如前所述,波函数相位没有梯度意味着正则动量为零
轴,虽然等相面没有偏转,但是粒子实际上却是偏转了。 在等相面上,如前所述,波函数相位没有梯度意味着正则动量为零 ,但是因为沿等相面方向有非零的
,但是因为沿等相面方向有非零的  ,因此电子的机械动量实际上并不为
,因此电子的机械动量实际上并不为 ,而是与电磁动量锁定的 (动量匹配 momentum matching ):
,而是与电磁动量锁定的 (动量匹配 momentum matching ):  (注意这个匹配成立的条件恰恰是波函数的等相面没有偏转)。当粒子沿x方向运动的时候,
(注意这个匹配成立的条件恰恰是波函数的等相面没有偏转)。当粒子沿x方向运动的时候, 越来越大,因此
越来越大,因此  也越来越大,也就是说粒子具有垂直于运动方向的加速度,这就是Lorentz 力。换言之就是因为有
也越来越大,也就是说粒子具有垂直于运动方向的加速度,这就是Lorentz 力。换言之就是因为有 的存在,因此对机械动量来说,波函数的等相面并不是“等相”的,而是会有一个沿着
的存在,因此对机械动量来说,波函数的等相面并不是“等相”的,而是会有一个沿着 的相位积累,所以机械动量看到等相面其实是偏转的。再或者我们可以不选取Landau规范而是对称规范
的相位积累,所以机械动量看到等相面其实是偏转的。再或者我们可以不选取Landau规范而是对称规范 ,那么就可以更方便看到同样的电子偏转结果而呈现Lorentz力。这也是必然的,因为规范自由度并不会影响真实物理过程。这就是量子力学层次上Lorentz力的起源。
,那么就可以更方便看到同样的电子偏转结果而呈现Lorentz力。这也是必然的,因为规范自由度并不会影响真实物理过程。这就是量子力学层次上Lorentz力的起源。
单从形式上看是多体波函数的形式构造 ,m是奇数是源于电子的交换反对称性,且是填充数倒数。正是Laughlin抓住了FQH系统的元激发的分数统计性质,才使得他的理论大获成功。实际上这种形式也正是决定了其分数统计性质;我们可以反过来看待,若先不考虑具体的Laughlin波函数形式,从二维的分数统计出来看,Laughlin波函数的形式是必然的。我们考察的量子多体系统的交换统计。在全同粒子系统中,交换两个粒子坐标的操作用置换群描写。置换群包含 两个元素,单位算子
整数量子统计:
分数量子统计:
在一般的量子统计中,我们从不考虑粒子交换的路径会对统计性质有什么影响。因为在三维空间,两个粒子无论以什么方式互相绕一圈,形成任意的闭合曲线,这条闭合曲线总可以连续收缩为一点,它们都是拓扑等价的,或说所有闭合曲线属于同一拓扑等价类。路径的不同不会对置换群的表示有任何影响。但在二维平面(空间),情况则截然不同。 考虑平面上的一条闭合曲线,该平面上它包围区域里有一个奇点。如果在三维空间中,这条曲线可以绕过奇点而收缩为一点,但如果在二维平面里,那么这条曲线在收缩过程中就不可避免地碰到这个点,从而永远无法收缩为一点。这 就造成了二维平面中置换两个粒子坐标时粒子所走过的路径并不属于同一等价类。因此必须对路径进行分类,这样一来置换群的概念也要推广以区分不同等价类的路径。
描述这一问题的标准数学语言是同伦群。同伦群的精确定义比较抽象,我们这里用一个简单的例子来说明。考虑二维平面,由于绕一个点N圈的所有闭合曲线都是拓扑等价的,可以把绕点N周的所有闭合曲线组成的等价类作为同伦群的一个元素,很容易验证它们满足群的定义。这个群叫一阶同伦群,也称为基本群。 N个全同粒子系统的二维位形空间非常复杂,这个位形空间的同伦群是个无限群。位形空间分成若干不相连的区域,路径分成不相连的分支,每个分支作为一个元素组成所谓的辫子群。直观地说,两个全同粒子在二维平面中运动,它们划过的世界线相互缠绕,编成一条辫子,编辫子的不同方式就构成辫子群的元素。与此对应,任意子系统的波函数的Hilbert空间不再是置换群的表示,而是辫子群的表示,也就是说,在二维平面里只用置换群对路径分类是不够的,必须用辫子群做进一步的考查。

现在以微分几何的角度来更细致地描述分数统计的数学结构。Hilbert空间中的波函数
见对应关系是
当然,在考虑一般的切丛时候,纤维的截面是矢量场,因此态矢才是截面整体抽象表示不依赖于坐标基矢,波函数只能说是截面的局域依赖于基矢表示。 不过我们要讨论二维(
考虑在

这里
展开写为:
这里定义两类基矢之间的转换函数为:
进一步的位置交换
在流形
引入一个联络
这样也就给出与辫子群同构的和乐群(给出一阶同伦群到规范群
鉴于我们只考察多体系统的统计性质,那么联络
由之前提出的联络平移条件得出:
解出
那么对于
波函数
自然得到Laughlin波函数形式
这里
如果比较Wilzeck的任意子模型的哈密顿量Hamiltonian和Chern-Simons场的作用量,会发现二者速途同归:前者是构造荷电带虚拟磁通的任意子,后者是荷电玻色子与Chern-Simons场耦合的结果。引入了C-S 场后,和荷电粒子耦合就会出现这种虚拟的磁通(规范势),
由此可见非零场强只定域在粒子世界线上,因此粒子间不存在经典的Lorentz力,这也就是为何称为虚拟规范势的原因。在二维平面上有磁通

Chern-Simons理论中的统计规范场没有独立的动力学自由度,因而并不描写有独立动力学的粒子,它的唯一作用在于给出分数统计所要求的额外相因子。从场方程可以明显地看出这一点:统计规范场的场量完全由物质流确定,因此它的方程确切地说是一个约束条件。引入Chern-Simons项另一个好处是可以清晰地讨论
II.拓扑不变量
QHE与陈数
我们已经知道Chern-Simons项是个拓扑不变量,其本质是第三陈类。那么回过头来我们发现量子霍尔效应的电导率包含的系数正是个第一陈类积分而得的陈数。

在上世纪80年代以前人们对物质状态进行分类的主要依据是体系的对称性。依据传统的相变理论。不同的量子态可以通过Landau自发对称性破缺的原理来理解,对称性由序参量描述对称性破缺意味着序参量不为零的有序相的出现。举例来说,晶体破坏了空间连续平移对称性;铁磁体破坏了空间旋转对称性;超导体破坏
在量子Hall效应中,人们研究时候发现其Hall电导系数正是刻画具有不同的拓扑有序态的系统必须由不同的拓扑不变量来进行描述拓扑序的量,具有拓扑不变性,就像某种“几何”内蕴的“示性数”;只不过这里的"几何"是在哈密顿量的赝自旋靶空间或者动量空间中诱导出来的纤维丛(Bloch丛)上(根据主丛的定义,就是

我们知道微分几何中有 “Gauss-Bonnet定理” : 对于一个无边界二维流形

Gauss-Bonnet定理是讨论的是几何流形的拓扑。而与
它就是

类比于光滑流形,进一步推广到纤维丛
曲率矩阵的不变多项式称为总陈类:
陈类在整个底流形上的积分(复向量丛
1982 年Thouless等人(TKNN)在一片奠基性文章中利用Kubo公式(线性响应理论)就算了二维周期性晶格系统的Hall电导发现其具有和Berry相一样的数学结构,因而进一步指出

Laughlin在对整数量子Hall效应时候,考虑到系统中的电子波函数整体相位相干性,引入横向周期性边界条件将位形空间构造成环带形状(torus:

实际的样品中,需要考虑存在杂质并束缚电子使之成为定域态,有掺杂的情况,每一Landau能级己扩展为能带(扩展边缘态)。一定范围内磁场变化时候电子落在定域束缚态中使得自由电子数目不增加,从而出现Hall电导平台。

以TKNN(Thouless-Kohmoto-Nightingale-deNijs) 拓扑不变量角度去阐述IQHE则是更现代的凝聚态理论。二维IQHE系统的有效场理论哈密顿量(Haldane模型)为:
解出的能谱中含有无能隙手征边缘态的谱线,其中的手性费米子不能反向散射,因而整数量子Hall系统是破坏时间反演对称的(Haldane哈密顿量中的磁场“质量”项使得零质量手征费米子激发破坏)。边界上的边缘态数量为:
*这里要顺带说一下,通俗的整数量子Hall效应的直观解释是这样说:电子在磁场中因为受到总是垂直于电子的运动方向的洛伦兹力,于是就形成一个圈。磁场很强的情况下,电子的轨道半径很小,因此电子都束缚在Landau态中成为束缚态,把所有这些轨道填满了就没地方可以去了(这也就是电子把逐个Landau能级填满)。但是当靠近样品边缘的时候,电子没有办法跑出一整个轨道了,于是只能沿着样品的边缘跳,画出一个接一个的半圆弧。也就是说,电流是可以沿着边缘传导的。而且因为电子只能沿着单一方向转圈,边缘上电流是“单行道”,只能沿一个方向传输,(也即上面所说的“手征边缘态”)。

这种经典解释的图像看起直观,但并真的不是量子力学里面所描述的图像:显然量子力学里面没有什么一个个固定的圆形轨道,我们之前就讨论过Landau能级,再次需要再次提醒大家注意这个才是真正的物理图景。但这个通俗直观的解释也有其精妙的地方:我们知道在量子力学中,动量算符为
*对于电子在磁场中的偏转运动的量子层面解释是和相位有关。这里首先不妨考虑Landau规范:
本文由Phantom_Ghost授权(果壳网)发表,文章著作权为原作者所有。
2条评论
自旋为1/2的粒子是什么形状的,三维真的有转两圈才能和自己重合的形状?
这个问题是不是说明了粒子内部是更高维度的空间?
按投票排序按时间排序
15 个回答
关键词:基本群,投影表示,周期边界条件。
要完整回答这个问题,涉及到的数学概念比较多。
首先,我们描述旋转,是用”旋转群“的概念,即群SO(3)。同时感兴趣的是这个群的李代数so(3),即量子力学里的角动量代数。
群和代数提供了两个角度切入这个问题:
1. 从群的角度。
首先,如果我们把旋转操作不看作一个群作用,而是一系列无穷小操作的组合,即转一圈相当于N次旋转(180/N)°,以示与”不转“的区别。这样,一个旋转就变成了群流形上的一条线(contour),任何回到原位(群单位元)的旋转体现为群流形上的一个圈(loop)。然后我们去看被转的对象:我们做以下识别(distinguish),即两个不同的旋转操作,对于任意对象而言,必然等同的条件是,它们所代表的contour之间同伦(这一结论适用于任意群)。对于转圈,则是它们所代表的loop同伦。”不转“即一个收缩至一点的loop,那么和”不转“等同的”转圈“,就必须能够(在群流形上)收缩至一点。如果假设群的实现是可微的,那么这样的识别是逻辑上可能的最细致的识别。
量子态可以做这种识别,因为它可以有内部自由度(比如相位)。经典态无法做这么细致的识别,因为它的自由度是固定的。
问题来了:SO(3)群的拓扑性质(形状)很特殊,是一个对径认同的球体,它上面有两类不等价的loop,其中一类等价于点(”不转“),而另一类和它并不等价,而”转一圈“这个操作就属于这个非平凡的类里面。简单来说,”转一圈“这个操作无法连续得变化为”不转“的操作(你可以试一试)。
数学上,这称为”SO(3)群的基本群是 ”。
”。
这有什么意义呢?当我们在量子理论中实现一个群操作时,允许这样的事情发生:

即群的表示 并不完全同构于群
并不完全同构于群 本身。这称为投影表示。这有点像一个
本身。这称为投影表示。这有点像一个 -orbifold。在SO(3)的情况下,这就是个
-orbifold。在SO(3)的情况下,这就是个 -orbifold,其定轴旋转的子流形就是一个莫比乌斯带(的边界) @杨晓堃 。
-orbifold,其定轴旋转的子流形就是一个莫比乌斯带(的边界) @杨晓堃 。
2. 从代数的角度。
这个角度就比较常见了,一般的量子力学书都是这么讲的。首先,so(3)=su(2),即两个群的李代数相同。然后,我们把这个代数称为角动量代数,并且写出它的所有表示。然后我们发现有自旋1/2的表示。这样的表示对于轨道角动量不适用的原因是波函数在实空间的单值性,导致了周期边界条件;而自旋角动量适用恰恰是因为它的旋转并不对应实空间的点,所以不需要有单值性,因此可以有反周期(anti-periodic)边界条件。
当然,这造成了很多人(比如题主)的困惑。简单把它归结于“自旋是内秉性质”不是一个很有说服力的方法,因为它其实还是来自于空间旋转。
两者的联系:
拥有相同的李代数的群SO(3)和SU(2),后者有着简单拓扑 ,而前者恰好是后者的某种automorphism的商集,过程中改变了拓扑,而这种automorphism则成了前者的基本群。因此,前者算上投影表示就和后者完全相同了。
,而前者恰好是后者的某种automorphism的商集,过程中改变了拓扑,而这种automorphism则成了前者的基本群。因此,前者算上投影表示就和后者完全相同了。
经 @flying zz 提醒,更好的说法是:拓扑上,SU(2)是SO(3)的universal cover,所以它们有相同的李代数但不同的拓扑,而且前者的所有表示和后者的所有投影表示完全相同。对于一般的群,应该也有如此性质。比如高维旋转群,Spin(n)就定义为SO(n)的universal cover。这就是为什么我们可以省略介绍投影表示,而直接使用群SU(2)=Spin(3)作为量子理论的旋转群,并给出多一倍的表示。
要完整回答这个问题,涉及到的数学概念比较多。
首先,我们描述旋转,是用”旋转群“的概念,即群SO(3)。同时感兴趣的是这个群的李代数so(3),即量子力学里的角动量代数。
群和代数提供了两个角度切入这个问题:
1. 从群的角度。
首先,如果我们把旋转操作不看作一个群作用,而是一系列无穷小操作的组合,即转一圈相当于N次旋转(180/N)°,以示与”不转“的区别。这样,一个旋转就变成了群流形上的一条线(contour),任何回到原位(群单位元)的旋转体现为群流形上的一个圈(loop)。然后我们去看被转的对象:我们做以下识别(distinguish),即两个不同的旋转操作,对于任意对象而言,必然等同的条件是,它们所代表的contour之间同伦(这一结论适用于任意群)。对于转圈,则是它们所代表的loop同伦。”不转“即一个收缩至一点的loop,那么和”不转“等同的”转圈“,就必须能够(在群流形上)收缩至一点。如果假设群的实现是可微的,那么这样的识别是逻辑上可能的最细致的识别。
量子态可以做这种识别,因为它可以有内部自由度(比如相位)。经典态无法做这么细致的识别,因为它的自由度是固定的。
问题来了:SO(3)群的拓扑性质(形状)很特殊,是一个对径认同的球体,它上面有两类不等价的loop,其中一类等价于点(”不转“),而另一类和它并不等价,而”转一圈“这个操作就属于这个非平凡的类里面。简单来说,”转一圈“这个操作无法连续得变化为”不转“的操作(你可以试一试)。
数学上,这称为”SO(3)群的基本群是
这有什么意义呢?当我们在量子理论中实现一个群操作时,允许这样的事情发生:
即群的表示
2. 从代数的角度。
这个角度就比较常见了,一般的量子力学书都是这么讲的。首先,so(3)=su(2),即两个群的李代数相同。然后,我们把这个代数称为角动量代数,并且写出它的所有表示。然后我们发现有自旋1/2的表示。这样的表示对于轨道角动量不适用的原因是波函数在实空间的单值性,导致了周期边界条件;而自旋角动量适用恰恰是因为它的旋转并不对应实空间的点,所以不需要有单值性,因此可以有反周期(anti-periodic)边界条件。
当然,这造成了很多人(比如题主)的困惑。简单把它归结于“自旋是内秉性质”不是一个很有说服力的方法,因为它其实还是来自于空间旋转。
两者的联系:
拥有相同的李代数的群SO(3)和SU(2),后者有着简单拓扑
经 @flying zz 提醒,更好的说法是:拓扑上,SU(2)是SO(3)的universal cover,所以它们有相同的李代数但不同的拓扑,而且前者的所有表示和后者的所有投影表示完全相同。对于一般的群,应该也有如此性质。比如高维旋转群,Spin(n)就定义为SO(n)的universal cover。这就是为什么我们可以省略介绍投影表示,而直接使用群SU(2)=Spin(3)作为量子理论的旋转群,并给出多一倍的表示。

No comments:
Post a Comment