统一路-6-奇妙的旋转1
|||
6. 奇妙的旋转(之一)
我们到处都能看到旋转的物体。铁路和公路上车轮滚滚,舞台上芭蕾舞演员频频转圈。宇宙中的星云,我们居住的地球,太阳系和银河系,这些天体都处于永恒而持久的旋转运动中。
物理学与各种旋转结下不解之缘,从力学中研究的刚体转动,到量子理论中的粒子自旋。地球绕太阳转,月亮绕地球转,滚珠在轴承滚道中转,电子绕原子核转,每一层次的实验和理论中似乎都少不了旋转。物理中的旋转除了在真实时空中的旋转之外,还有一大部分是在假想的、抽象的空间中的旋转,比如动量空间,希尔伯特空间,自旋空间、同位旋空间等。
在上一篇文章中我们介绍了群论的基本概念,空间中的旋转也构成群,并且,旋转群是物理中非常重要的一类群。旋转群有离散的和连续的之分。连续旋转群具有天然的流形结构,是一种李群,理论物理,特别是统一理论中所感兴趣的旋转李群有SO(3)、SO(2)、U(1)、SU(2)、SU(3)等等。
旋转可以用大家熟知的矩阵来表示。因此,我们首先用矩阵的语言,解释一下上面所列的一串符号是什么意思:括号中的数目字(3、2、1)等是表示旋转的矩阵空间的维数;大写字母O(Orthogonal)代表正交矩阵;U(Unitary)代表酉矩阵;S(Special)是特殊的意思,表示矩阵的行列式为1。
比如,举三维空间的旋转群O(3)为例。这儿3是指旋转空间的维数,O对应于保持长度和角度不变的正交变换矩阵。具体一点说,正交矩阵O(3)是一个由3X3=9个实数组成的矩阵,它的3个列向量或者3个行向量,都构成3维空间中3个正交的单位矢量。一般来说,正交矩阵O(3)的行列式可为1或-1。当行列式为-1时,正交矩阵表示的变换是旋转再加反演,这儿的负号便来自反演。上面所述的是O(3)旋转群,如果加上字母S,指的便是特殊旋转群SO(3),那意味着,矩阵行列式被限制为1。所以,SO(3)表示的是3维空间中无反演的纯粹旋转。
物理学中的量子理论与复数关联密切,因此,我们将正交群的概念从实数扩展到复数,正交矩阵在复数域中的对应物叫做酉矩阵,正交群O(n)便扩展成为元素为复数的酉群U(n)。酉矩阵的行列式一般来说也是一个复数。行列式限制为实数1的酉群被称为特殊酉群,记为SU(n)。举例之:U(1)是1维复数空间的旋转群;SU(2)和SU(3)分别是2维和3维复数空间的特殊旋转群。
李群是由有限个实数参数的连续变化而生成的连续群。因而,上面列举的旋转李群既具有群的结构,又是参数空间的光滑流形。数学上“光滑”的意思表示无穷可微。如上所述,旋转李群的“群”的性质,可从研究相应的矩阵表示而得到。那么,它们作为“流形”的一面又如何呢?首先让我们看看图6-1所示的李群U(1)的图形。
根据酉群的定义,U(1)由1X1的所有酉矩阵,即模为1的所有复数所组成。尽管这个复数的模被限制为1,但幅角还可以任意变化,所以U(1)是由复数平面上所有长度为1的矢量绕着原点转动而构成的。如图6-1b中所示,复数平面单位圆上的一个转动可用点Z表示,复数Z的所有集合在复数乘法下构成群,在几何上则形成图中的单位圆。这个圆便是李群U(1)的流形,幅角是连续变化的实数参数。这个流形是连通的,但不是单连通的。不是单连通意味着流形上存在不能连续地收缩到一个点的闭曲线(图6-2)。图上的那个圆周就是U(1)上的一条闭曲线,它显然不能连续地收缩到一个点,由此表明U(1)不是单连通的。
所以, SO(2) 与U(1)同构,它们的流形都是1维的,是单位圆。李群流形的维数也叫做李群的阶数,等于构成流形的独立参数的个数,与旋转所在空间的维数是两码事。比如SO(2)是2维空间的旋转,对应的旋转矩阵是2X2的,但作为李群,它只需要1个参数(转角)来表示,因而是1阶李群。见图6-1c右下角的2X2矩阵,矩阵是2维的,但参数只有一个:f,流形是1维的。
二维实数空间的SO(2)特殊旋转群与一维复数平面上的旋转群U(1)同构。那么,维数高一阶的实数和复数旋转群之间是否也有类似的关系呢?比SO(2)维数高1维的是SO(3),比U(1) 高1维的是U(2)。这两类旋转群的关系究竟如何?
首先研究我们所熟悉的三维实空间的旋转,它对应于SO(3) 群。欧拉证明过一个欧拉旋转定理,说的是任何一个三维旋转,都可以表示成一个固定方向的转轴加上绕此转轴的转动。转轴的方向需要两个实数参数决定,绕着该轴旋转的角度则是第三个参数,所以,群SO(3)中的元素可以用三个实参数表示。比如我们通常所用的欧拉角表示法,a、b、g就是三个不同的参数,其中a从0变到2p;b从0变到p;g从0变到2p,见图6-3a。独立参数的个数为3,所以,李群SO(3)的阶数等于3。
而U(2)群描述的是2维复数平面上的旋转,一个复数由两个实数组成,两个复数便有4个独立的实数变量,这样,U(2)的阶数为4,不同于SO(3)的阶数3。但是,如果考虑特殊酉群SU(2),它需要满足“模为1”的条件,这样便使得独立变量数目减少了1个,成为3。因此,SU(2)与SO(3)的阶数相同,都是3维流形,通常我们便将这两个连续群进行比较。
因为是3个参数,所以SO(3)的流形是个3维空间,但整体而言却不同于简单的欧氏空间。如果是2个参数构成的2维流形的话,我们还有可能用嵌入3维空间中的曲面画出来。但对SO(3)这种流形本身是3维空间的情况,需要将它嵌入4维或更高维数的空间中,成为其中的一个三维超曲面!那种图形,我们可怜的大脑实在难以想象。
不过,数学家和物理学家们仍然对SO(3) 及SU(2)作了很多研究,确定了它们的流形的许多基本几何性质【1】。比如,尽管SO(3)流形的直观图像无法画出,但可以证明它是连通的,却不是单连通的(有关连通图形,见图6-2),这一点性质与图6-1中SO(2) 的圆圈类似。
因为一个三维旋转可以表示成一个固定方向的转轴加上绕此转轴的旋转角,旋转角取值从+p到-p。因此,我们可以将这个转动对应于一个半径小于或等于p的3维实心球中的一个点,如图6-3b所示的A、B、C等等点。这个点与球心所成矢量的方向,表示转动轴的方向,矢量的长度,则表示转角的大小。比如,位于球面上的A点,可以表示绕着OA顺时针旋转180度(p),A’点便表示绕着OA逆时针旋转180度。而位于该实心球内部的B点和C点,对应的则是绕着相应转动轴的小于180度的旋转(旋转角g< p)。
因此,这个实心球可以看作是SO(3) 的流形。不过还有一个问题:绕一个给定轴转动p,等于绕相反方向的轴转动-p。所以,球面p上的每个点,与它的反方向的对应点,表示的是同一个点。比如图6-3b中的A和A’,实际上表示的是同一个转动。因此,这样的两个点应该被粘在一起!仅仅将A和A’粘在一起还可以想象,要将球面上所有的直径端点都如此粘起来,就又感觉脑细胞不够用了。不过无论如何,到此为止,我们对SO(3)的拓扑结构已经有了一点点了解。
那么,SO(3)和SU(2)到底是什么关系呢?SU(2)是二维复数空间中模为1的旋转群,可以用图6-3c所示的2维复数矩阵来表示。SU(2)的酉矩阵与SO(3)实心球中的点是2对1的关系。如果SU(2)的一个元素,例如图c中的U,对应于SO(3)中的C点(图6-3b)的话,变换(-U)也对应于同样的C点。换言之, 3维空间的一个旋转,对应于复数空间两个幺模旋转。用群论的语言来说:SU(2)与SO(3)两群间存在2:1的同态关系。注意,这儿所谓的“2:1同态”,有点类似于刚才家庭结构比喻中的张家和陈家。同构是一一对应的同态。
无论如何,人脑直观想象几何图像的能力毕竟有限。当几何图形画出不来的时候,“代数”可以来帮忙。对于李群流形的研究也是这样,可以请来它的同宗兄弟“李代数”助阵。因此,下一节中我们仍然以这几个旋转群为例,对李群上的“李代数”略作介绍。(待续)
(物理学从爱因斯坦的统一梦,走到规范理论、标准模型等等,少不了数学。因此,这几篇文章,都是介绍一些所需要的数学及量子力学方面的基础知识,为顺利打通统一之路扫去障碍,铺平道路。)
参考资料:
我们到处都能看到旋转的物体。铁路和公路上车轮滚滚,舞台上芭蕾舞演员频频转圈。宇宙中的星云,我们居住的地球,太阳系和银河系,这些天体都处于永恒而持久的旋转运动中。
物理学与各种旋转结下不解之缘,从力学中研究的刚体转动,到量子理论中的粒子自旋。地球绕太阳转,月亮绕地球转,滚珠在轴承滚道中转,电子绕原子核转,每一层次的实验和理论中似乎都少不了旋转。物理中的旋转除了在真实时空中的旋转之外,还有一大部分是在假想的、抽象的空间中的旋转,比如动量空间,希尔伯特空间,自旋空间、同位旋空间等。
在上一篇文章中我们介绍了群论的基本概念,空间中的旋转也构成群,并且,旋转群是物理中非常重要的一类群。旋转群有离散的和连续的之分。连续旋转群具有天然的流形结构,是一种李群,理论物理,特别是统一理论中所感兴趣的旋转李群有SO(3)、SO(2)、U(1)、SU(2)、SU(3)等等。
旋转可以用大家熟知的矩阵来表示。因此,我们首先用矩阵的语言,解释一下上面所列的一串符号是什么意思:括号中的数目字(3、2、1)等是表示旋转的矩阵空间的维数;大写字母O(Orthogonal)代表正交矩阵;U(Unitary)代表酉矩阵;S(Special)是特殊的意思,表示矩阵的行列式为1。
比如,举三维空间的旋转群O(3)为例。这儿3是指旋转空间的维数,O对应于保持长度和角度不变的正交变换矩阵。具体一点说,正交矩阵O(3)是一个由3X3=9个实数组成的矩阵,它的3个列向量或者3个行向量,都构成3维空间中3个正交的单位矢量。一般来说,正交矩阵O(3)的行列式可为1或-1。当行列式为-1时,正交矩阵表示的变换是旋转再加反演,这儿的负号便来自反演。上面所述的是O(3)旋转群,如果加上字母S,指的便是特殊旋转群SO(3),那意味着,矩阵行列式被限制为1。所以,SO(3)表示的是3维空间中无反演的纯粹旋转。

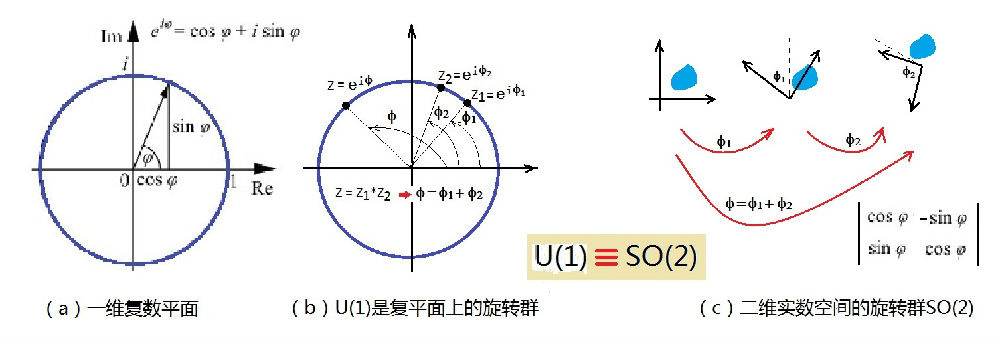
图6-1:U(1)群和SO(2)群
有一个比SO(3)更简单的特殊旋转群,是SO(3)的李子群,对应于2维空间中的旋转:SO(2)。物理学中的量子理论与复数关联密切,因此,我们将正交群的概念从实数扩展到复数,正交矩阵在复数域中的对应物叫做酉矩阵,正交群O(n)便扩展成为元素为复数的酉群U(n)。酉矩阵的行列式一般来说也是一个复数。行列式限制为实数1的酉群被称为特殊酉群,记为SU(n)。举例之:U(1)是1维复数空间的旋转群;SU(2)和SU(3)分别是2维和3维复数空间的特殊旋转群。
李群是由有限个实数参数的连续变化而生成的连续群。因而,上面列举的旋转李群既具有群的结构,又是参数空间的光滑流形。数学上“光滑”的意思表示无穷可微。如上所述,旋转李群的“群”的性质,可从研究相应的矩阵表示而得到。那么,它们作为“流形”的一面又如何呢?首先让我们看看图6-1所示的李群U(1)的图形。
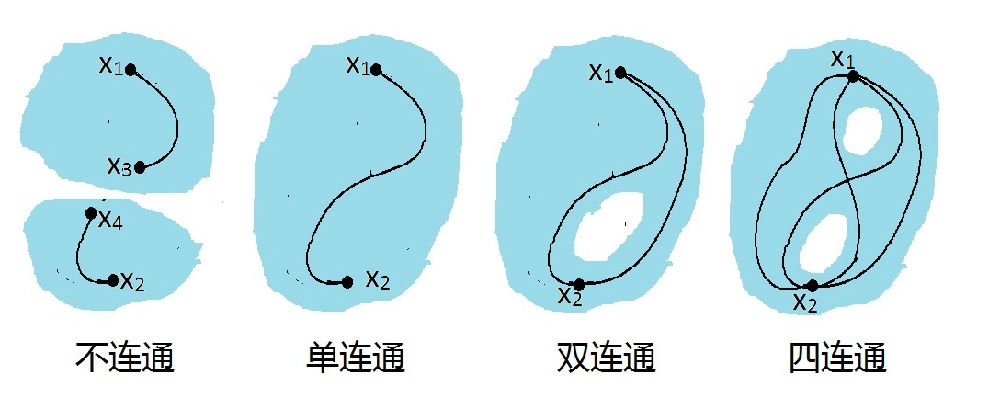
根据酉群的定义,U(1)由1X1的所有酉矩阵,即模为1的所有复数所组成。尽管这个复数的模被限制为1,但幅角还可以任意变化,所以U(1)是由复数平面上所有长度为1的矢量绕着原点转动而构成的。如图6-1b中所示,复数平面单位圆上的一个转动可用点Z表示,复数Z的所有集合在复数乘法下构成群,在几何上则形成图中的单位圆。这个圆便是李群U(1)的流形,幅角是连续变化的实数参数。这个流形是连通的,但不是单连通的。不是单连通意味着流形上存在不能连续地收缩到一个点的闭曲线(图6-2)。图上的那个圆周就是U(1)上的一条闭曲线,它显然不能连续地收缩到一个点,由此表明U(1)不是单连通的。

图6-2:各种连通情况
一个复数由两个实数组成,复数平面上的转动实际上与2维实数平面上的转动一一对应。这个对应将U(1)群与SO(2)群关联起来,可以证明,U(1)与SO(2)是同构的。两个群同构的意思可以粗糙地理解为通常意义下所说的“相同结构”。也就是说,忽略组成每一个群的元素的具体属性、乘法操作的具体规定等等,仅仅将“群”的结构性质“抽”出来比较,两个群是相同的。插进一段通俗的比喻,也许可以使你更好地理解“同构”(比喻的例子不是群同构!):两个3口之家,陈家和李家,都由父、母、子组成。如果我们只感兴趣研究每个家庭成员的性别及相互关系这种结构的话,可以说这两个家庭是“同构”的。尽管陈妈妈已经60岁,李家儿子刚出生,这些细节都无所谓,我们运用数学“抽象”,只看我们需要看的结构,从而认定两个家庭是“同构”的。而具体的陈家和李家,只不过是这种结构的两个不同的具体表示而已。再进一步,如果另有张姓两兄弟,都有老婆儿子,但大家住一起组成6口人的“张家”。那么显然的,陈家和张家不同构。所以, SO(2) 与U(1)同构,它们的流形都是1维的,是单位圆。李群流形的维数也叫做李群的阶数,等于构成流形的独立参数的个数,与旋转所在空间的维数是两码事。比如SO(2)是2维空间的旋转,对应的旋转矩阵是2X2的,但作为李群,它只需要1个参数(转角)来表示,因而是1阶李群。见图6-1c右下角的2X2矩阵,矩阵是2维的,但参数只有一个:f,流形是1维的。
二维实数空间的SO(2)特殊旋转群与一维复数平面上的旋转群U(1)同构。那么,维数高一阶的实数和复数旋转群之间是否也有类似的关系呢?比SO(2)维数高1维的是SO(3),比U(1) 高1维的是U(2)。这两类旋转群的关系究竟如何?
首先研究我们所熟悉的三维实空间的旋转,它对应于SO(3) 群。欧拉证明过一个欧拉旋转定理,说的是任何一个三维旋转,都可以表示成一个固定方向的转轴加上绕此转轴的转动。转轴的方向需要两个实数参数决定,绕着该轴旋转的角度则是第三个参数,所以,群SO(3)中的元素可以用三个实参数表示。比如我们通常所用的欧拉角表示法,a、b、g就是三个不同的参数,其中a从0变到2p;b从0变到p;g从0变到2p,见图6-3a。独立参数的个数为3,所以,李群SO(3)的阶数等于3。
而U(2)群描述的是2维复数平面上的旋转,一个复数由两个实数组成,两个复数便有4个独立的实数变量,这样,U(2)的阶数为4,不同于SO(3)的阶数3。但是,如果考虑特殊酉群SU(2),它需要满足“模为1”的条件,这样便使得独立变量数目减少了1个,成为3。因此,SU(2)与SO(3)的阶数相同,都是3维流形,通常我们便将这两个连续群进行比较。

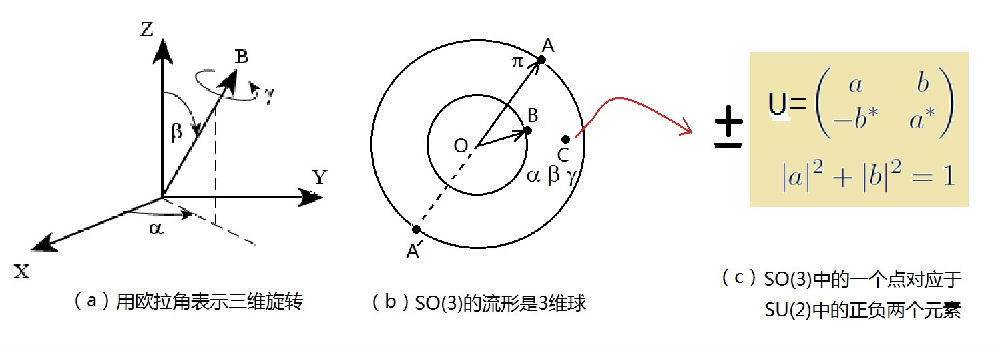
图6-3:SO(3)和SU(2)
图6-1所示的U(1)(或SO(2))群足够简单,其流形能够用一个圆周表示出来,而三维空间旋转群SO(3)的流形就难以用图形画出来了。因为是3个参数,所以SO(3)的流形是个3维空间,但整体而言却不同于简单的欧氏空间。如果是2个参数构成的2维流形的话,我们还有可能用嵌入3维空间中的曲面画出来。但对SO(3)这种流形本身是3维空间的情况,需要将它嵌入4维或更高维数的空间中,成为其中的一个三维超曲面!那种图形,我们可怜的大脑实在难以想象。
不过,数学家和物理学家们仍然对SO(3) 及SU(2)作了很多研究,确定了它们的流形的许多基本几何性质【1】。比如,尽管SO(3)流形的直观图像无法画出,但可以证明它是连通的,却不是单连通的(有关连通图形,见图6-2),这一点性质与图6-1中SO(2) 的圆圈类似。
因为一个三维旋转可以表示成一个固定方向的转轴加上绕此转轴的旋转角,旋转角取值从+p到-p。因此,我们可以将这个转动对应于一个半径小于或等于p的3维实心球中的一个点,如图6-3b所示的A、B、C等等点。这个点与球心所成矢量的方向,表示转动轴的方向,矢量的长度,则表示转角的大小。比如,位于球面上的A点,可以表示绕着OA顺时针旋转180度(p),A’点便表示绕着OA逆时针旋转180度。而位于该实心球内部的B点和C点,对应的则是绕着相应转动轴的小于180度的旋转(旋转角g< p)。
因此,这个实心球可以看作是SO(3) 的流形。不过还有一个问题:绕一个给定轴转动p,等于绕相反方向的轴转动-p。所以,球面p上的每个点,与它的反方向的对应点,表示的是同一个点。比如图6-3b中的A和A’,实际上表示的是同一个转动。因此,这样的两个点应该被粘在一起!仅仅将A和A’粘在一起还可以想象,要将球面上所有的直径端点都如此粘起来,就又感觉脑细胞不够用了。不过无论如何,到此为止,我们对SO(3)的拓扑结构已经有了一点点了解。
那么,SO(3)和SU(2)到底是什么关系呢?SU(2)是二维复数空间中模为1的旋转群,可以用图6-3c所示的2维复数矩阵来表示。SU(2)的酉矩阵与SO(3)实心球中的点是2对1的关系。如果SU(2)的一个元素,例如图c中的U,对应于SO(3)中的C点(图6-3b)的话,变换(-U)也对应于同样的C点。换言之, 3维空间的一个旋转,对应于复数空间两个幺模旋转。用群论的语言来说:SU(2)与SO(3)两群间存在2:1的同态关系。注意,这儿所谓的“2:1同态”,有点类似于刚才家庭结构比喻中的张家和陈家。同构是一一对应的同态。
无论如何,人脑直观想象几何图像的能力毕竟有限。当几何图形画出不来的时候,“代数”可以来帮忙。对于李群流形的研究也是这样,可以请来它的同宗兄弟“李代数”助阵。因此,下一节中我们仍然以这几个旋转群为例,对李群上的“李代数”略作介绍。(待续)
(物理学从爱因斯坦的统一梦,走到规范理论、标准模型等等,少不了数学。因此,这几篇文章,都是介绍一些所需要的数学及量子力学方面的基础知识,为顺利打通统一之路扫去障碍,铺平道路。)
参考资料:
【1】Gelfand,I.M.; Minlos, R.A.; Shapiro, Z.Ya. (1963), Representations of the Rotation andLorentz Groups and their Applications, New York: Pergamon Press
No comments:
Post a Comment