布朗运动01:朗之万方程 其中势函数 在平衡态附近就是自由能,而在某些远离平衡的定常态附近也可以从微观运动方程的时间反演对称出
把时间离散化为步长殼t 的小段,令
t=n殼t,同时保持殼t 适当大,使得每小段时间头尾
的运动彼此无关,于是行走n 步的结果xn 就是n 个
独立随机变量之和
t=n殼t,同时保持殼t 适当大,使得每小段时间头尾
的运动彼此无关,于是行走n 步的结果xn 就是n 个
独立随机变量之和
爱因斯坦关系[编辑]
维基百科,自由的百科全书
在分子运动论中,爱因斯坦关系是一个以前没有想到的关系,由阿尔伯特·爱因斯坦在1905年和Marian Smoluchowski在1906年独立发现:
 是玻尔兹曼常数,T是绝对温度。
是玻尔兹曼常数,T是绝对温度。
迁移率μp是粒子的终极速度与作用力之比:μp = vd / F。
这个方程是涨落耗散定理的一个早期的例子。它在电致扩散的现象中经常使用。
 是阻力系数
是阻力系数 的倒数。对于半径为
的倒数。对于半径为 的球形粒子,斯托克斯定律给出:
的球形粒子,斯托克斯定律给出:
 是介质的黏度。因此爱因斯坦关系变为:
是介质的黏度。因此爱因斯坦关系变为:
 ~10-10 m² s-1,假设蛋白质的密度是“标准”的~1.2 103 kg m-3。
~10-10 m² s-1,假设蛋白质的密度是“标准”的~1.2 103 kg m-3。
 与载流子的电荷q的乘积:
与载流子的电荷q的乘积:
 是化学势,p是粒子数。
是化学势,p是粒子数。
 是玻尔兹曼常数,T是绝对温度。
是玻尔兹曼常数,T是绝对温度。迁移率μp是粒子的终极速度与作用力之比:μp = vd / F。
这个方程是涨落耗散定理的一个早期的例子。它在电致扩散的现象中经常使用。
粒子的扩散[编辑]
在低雷诺数的极限下,迁移率 是阻力系数
是阻力系数 的倒数。对于半径为
的倒数。对于半径为 的球形粒子,斯托克斯定律给出:
的球形粒子,斯托克斯定律给出: 是介质的黏度。因此爱因斯坦关系变为:
是介质的黏度。因此爱因斯坦关系变为: ~10-10 m² s-1,假设蛋白质的密度是“标准”的~1.2 103 kg m-3。
~10-10 m² s-1,假设蛋白质的密度是“标准”的~1.2 103 kg m-3。电传导[编辑]
当应用于电传导的时候,通常把电迁移率定义为机械导纳 与载流子的电荷q的乘积:
与载流子的电荷q的乘积: 是化学势,p是粒子数。
是化学势,p是粒子数。
回答: 如果强行维持使物理系统处于不平衡状态的外界条件,例如温度差、浓度差、电位差(可把它们看作是广义力,记作 ),但又不使其离开平衡太 由 marketreflections 于 2011-03-01 04:57:41
菲克定律[编辑]
菲克定律描述擴散作用,可以使用這條定律來求得擴散係數,D。定律由阿道夫·菲克於1855年推導出來。
 的大小取決於溫度、流體黏度與分子大小,並與擴散分子流動的平均速度平方成正比。在稀的水溶液中,大部分離子的擴散係數都相近,在室溫下其數值大概在0.6×10-9至2×10-9 m2/s。而生物分子的擴散係數一般介於10-11及10-12 m2/s之間。
的大小取決於溫度、流體黏度與分子大小,並與擴散分子流動的平均速度平方成正比。在稀的水溶液中,大部分離子的擴散係數都相近,在室溫下其數值大概在0.6×10-9至2×10-9 m2/s。而生物分子的擴散係數一般介於10-11及10-12 m2/s之間。
在二維或以上的情況下,我們必須使用 (劈形或梯度算子)來把第一導數通用化,得
(劈形或梯度算子)來把第一導數通用化,得
 ,而對理想混合物而言,這股驅動力就是濃度的梯度。在非理想溶液或混合物的化學系統中,每一種物質的擴散驅動力則為各自種類的化學勢梯度。此時菲克第一定律(一維狀況)為:
,而對理想混合物而言,這股驅動力就是濃度的梯度。在非理想溶液或混合物的化學系統中,每一種物質的擴散驅動力則為各自種類的化學勢梯度。此時菲克第一定律(一維狀況)為:
對於二維或以上的擴散,其菲克第二定律為:
若擴散常數不是常數,但大小取決於座標及/或濃度,則菲克第二定律為:
 處於穩定態的時候,即濃度不會因時間而變動,因此方程的左邊等於零。在D不變及一維的情況下,濃度會隨位置x作線性的變動。在二維或以上情況則:
處於穩定態的時候,即濃度不會因時間而變動,因此方程的左邊等於零。在D不變及一維的情況下,濃度會隨位置x作線性的變動。在二維或以上情況則:
 的邊界上,該點濃度值為
的邊界上,該點濃度值為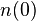 ,則擴散情況為
,則擴散情況為
 為擴散長度,用於量度濃度在x方向在時間t後傳播了多遠。
為擴散長度,用於量度濃度在x方向在時間t後傳播了多遠。
互補誤差函數在泰勒級數展開後的首兩項,可被用作的該函數的快捷近似:
菲克的實驗(模仿格雷姆的實驗)主要由兩個鹽槽組成,兩個槽由多條含水的管道連接,實驗量度水管中的鹽濃度及通量。有一點值得注意的是,菲克主要研究的是液體的擴散,而不是固體,因為當時普遍認為固體擴散並不可行[3]。時至今日,在研究固體、液體及氣體擴散(假設後兩者不會有大團的流體運動)時,菲克定律還是我們理解的核心。當擴散不遵從菲克定律時(確實有這種情況),我們把這種過程稱為“非菲克擴散”,把它們稱作例外的這點,“證實”了菲克於1855年提出的定律的重要性。
菲克第一定律在輻射傳送方程中也是有重要性的。然而,當擴散係數很小的時候,輻射被光速所限制,而不是被物質的抵抗力所限制,菲克第一定律與輻射傳送方程的關係就不準確。在這個時候可以採取通量限制。
在計算氣體通過流體膜的交換率時,可將上式及格雷姆定律一起運用。
有意思的是,漲落水動力方程含有一個描述菲克流的項,內有擴散係數,還有描述漲落的隨機項及水動力方程。在使用微擾手法計算漲落時,其零度近似就菲克定律。通過第一度近似可得漲落,然後漲落造成擴散。因為這個由低度近似描述的現象是高度近似的結果,所以某程度上這代表一個永真式。只須把水動力方程重整化就可以解決這個問題。
在某些情況下,解方程用的邊界條件為擴散時源頭濃度不變、有限源頭濃度或邊界會移動。
维基百科,自由的百科全书
目录
[隐藏]菲克第一定律[编辑]
假設從高濃度區域往低濃度流的通量大小與濃度梯度(空間導數)成正比,通過這個假設,菲克第一定律把擴散通量與濃度聯繫起來。在一維空間下的菲克定律如下: 為“擴散通量”(於某單位時間內通過某單位面積的物質量),例如
為“擴散通量”(於某單位時間內通過某單位面積的物質量),例如 。
。 量度在一段短時間內物質流過一小面積的量。
量度在一段短時間內物質流過一小面積的量。
 為擴散係數或擴散度,其量綱為[長度2 時間−1],例如
為擴散係數或擴散度,其量綱為[長度2 時間−1],例如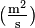
 為濃度(假設為理想混合物),其量綱為[(物質的量) 長度−3],例如
為濃度(假設為理想混合物),其量綱為[(物質的量) 長度−3],例如
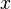 為位置[長度],例如
為位置[長度],例如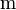
 的大小取決於溫度、流體黏度與分子大小,並與擴散分子流動的平均速度平方成正比。在稀的水溶液中,大部分離子的擴散係數都相近,在室溫下其數值大概在0.6×10-9至2×10-9 m2/s。而生物分子的擴散係數一般介於10-11及10-12 m2/s之間。
的大小取決於溫度、流體黏度與分子大小,並與擴散分子流動的平均速度平方成正比。在稀的水溶液中,大部分離子的擴散係數都相近,在室溫下其數值大概在0.6×10-9至2×10-9 m2/s。而生物分子的擴散係數一般介於10-11及10-12 m2/s之間。在二維或以上的情況下,我們必須使用
 (劈形或梯度算子)來把第一導數通用化,得
(劈形或梯度算子)來把第一導數通用化,得 。
。
 ,而對理想混合物而言,這股驅動力就是濃度的梯度。在非理想溶液或混合物的化學系統中,每一種物質的擴散驅動力則為各自種類的化學勢梯度。此時菲克第一定律(一維狀況)為:
,而對理想混合物而言,這股驅動力就是濃度的梯度。在非理想溶液或混合物的化學系統中,每一種物質的擴散驅動力則為各自種類的化學勢梯度。此時菲克第一定律(一維狀況)為:菲克第二定律[编辑]
菲克第二定律預測擴散會如何使得濃度隨時間改變: 為濃度,其量綱為[(物質的量) 長度−3],例如
為濃度,其量綱為[(物質的量) 長度−3],例如
 為時間[s]
為時間[s] 為擴散係數,其量綱為[長度2 時間−1],例如
為擴散係數,其量綱為[長度2 時間−1],例如
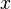 為位置[長度],例如
為位置[長度],例如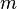
對於二維或以上的擴散,其菲克第二定律為:
 ,
,
若擴散常數不是常數,但大小取決於座標及/或濃度,則菲克第二定律為:
 處於穩定態的時候,即濃度不會因時間而變動,因此方程的左邊等於零。在D不變及一維的情況下,濃度會隨位置x作線性的變動。在二維或以上情況則:
處於穩定態的時候,即濃度不會因時間而變動,因此方程的左邊等於零。在D不變及一維的情況下,濃度會隨位置x作線性的變動。在二維或以上情況則:例:一維解(擴散長度)[编辑]
在一維(x軸)擴散的情況下,設時間為t,初始點位於 的邊界上,該點濃度值為
的邊界上,該點濃度值為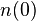 ,則擴散情況為
,則擴散情況為-
 。
。
 為擴散長度,用於量度濃度在x方向在時間t後傳播了多遠。
為擴散長度,用於量度濃度在x方向在時間t後傳播了多遠。互補誤差函數在泰勒級數展開後的首兩項,可被用作的該函數的快捷近似:
歷史[编辑]
生理學家阿道夫·菲克最早於1855年發表[1][2]他那著名的定律,這定律支配所有通過擴散所進行的質量運輸。菲克的研究受到之前托馬斯·格雷姆的實驗所啟發,但這些實驗就差在沒有提出任何基礎定律,而菲克就因提供了這樣的定律而聞名。菲克定律與同時代的其他著名科學家所發現的定律有近似的地方:達西定律(水流)、歐姆定律(電荷運輸)、及傅立葉定律(熱運輸)。菲克的實驗(模仿格雷姆的實驗)主要由兩個鹽槽組成,兩個槽由多條含水的管道連接,實驗量度水管中的鹽濃度及通量。有一點值得注意的是,菲克主要研究的是液體的擴散,而不是固體,因為當時普遍認為固體擴散並不可行[3]。時至今日,在研究固體、液體及氣體擴散(假設後兩者不會有大團的流體運動)時,菲克定律還是我們理解的核心。當擴散不遵從菲克定律時(確實有這種情況),我們把這種過程稱為“非菲克擴散”,把它們稱作例外的這點,“證實”了菲克於1855年提出的定律的重要性。
應用[编辑]
不同領域在需要模擬運輸過程時,普遍地都會用到各種基於菲克定律的方程,這些領域包括食品、神經元、生物聚合物、藥劑、有孔土壤、族群動態及半導體摻雜過程等。所有電壓電流測定法的方法都是基於菲克方程的解。聚合物科學及食品科學的大量實驗研究指出,在玻璃轉化下需要使用更通用的手法來描述運輸的分量。在玻璃轉化發生時,周圍的流動會變得“非菲克”。生物學上的應用[编辑]
從第一定律可得下式[4]:菲克第一定律在輻射傳送方程中也是有重要性的。然而,當擴散係數很小的時候,輻射被光速所限制,而不是被物質的抵抗力所限制,菲克第一定律與輻射傳送方程的關係就不準確。在這個時候可以採取通量限制。
在計算氣體通過流體膜的交換率時,可將上式及格雷姆定律一起運用。
液體的菲克流[编辑]
當兩種互溶液體接觸時,擴散發生,宏觀(或平均)濃度會跟隨菲克定律而定。在介觀角度下,也就是介於菲克定律所描述的宏觀及分子的微觀(分子隨機運動發生的比例)的角度下,我們不可以忽略漲落。這個時候可以使用蘭道-李佛西茲漲落水動力學來進行模擬。在這個理論框架下,擴散的起因是漲落,這些漲落的大小可由分子比例至宏觀比例[5]。有意思的是,漲落水動力方程含有一個描述菲克流的項,內有擴散係數,還有描述漲落的隨機項及水動力方程。在使用微擾手法計算漲落時,其零度近似就菲克定律。通過第一度近似可得漲落,然後漲落造成擴散。因為這個由低度近似描述的現象是高度近似的結果,所以某程度上這代表一個永真式。只須把水動力方程重整化就可以解決這個問題。
半導體生產上的應用[编辑]
不少生產半導體的技術及成型過程都有用到由菲克定律所得出的擴散方程,這些技術包括化學氣相沉積(CVD)、熱氧化、濕式氧化法及滲雜等。在某些情況下,解方程用的邊界條件為擴散時源頭濃度不變、有限源頭濃度或邊界會移動。
标签: 杂谈 |
由爱因斯坦、斯莫鲁霍夫斯基(M.Smoluchowski)等人在20世纪初开始的布朗运动理论,在一百年间发展出内容丰富的众多学科分支,现在正在成为分析生物细胞内分子机器运作原理的有力工具。爱因斯坦1905年发表的5篇论文中,关于布朗运动的文章可能人们知道得最少,而实际上它被引用的次数却超过了狭义相对论。
1
英国植物学家罗伯特·布朗在1828年和1829年的《哲学》杂志上发表了两篇文章,描述自己在1927年夏天在显微镜下观察到花粉颗粒在液体中的不停顿的运动。他最初曾经以为是看到了生命运动,但后来确认这种运动对细小的有机和无机颗粒都存在,因而不是生命现象所致。布朗认为运动的原因在于这些颗粒包含着“活性分子”(active molecules),而与所处液体没有关系。
事实上,布朗并不是观察到这类运动的第一人。他在上述两篇文章里就曾提到了约十位前人,包括做过大量观察的制作显微镜的巧手列文胡克(Antonnie von Leeuwenhock)。
2
爱因斯坦在1901—1905年期间致力于博士论文研究。他1905年发表的头一篇文章——“分子大小的新测定”就基于其博士论文。爱因斯坦考察了液体中悬浮粒子对渗透压的贡献,把流体力学方法和扩散理论结合起来,建议了测量分子尺寸和阿佛伽德罗常数的新办法。这样的研究同布朗运动发生关系是很自然的。然而,他1905年5月撰写的第二篇论文的题目并没有提及布朗运动。这篇题为《热的分子运动论所要求的静止液体中悬浮小粒子的运动》的文章,一开始就说:“可能,这里所讨论的运动就是所谓的布朗分子运动;可是,关于后者我所能得到唯一的资料是如此的不准确,以致在这个问题上我无法形成判断。”
爱因斯坦确实建立了布朗运动的分子理论,并且开启了借助随机过程描述自然现象的数理科学发展方向。
我们不在此重复爱因斯坦当年对扩散系数D的推导,直接从熟知的(一维)扩散方程出发:
3
如果把时间离散化为步长Δt的小段,令t=nΔt,同时保持Δt适当的大,使得每小段时间头尾的运动彼此无关,于是行走n步的结果xn就是n个独立随机变量之和。自然:
离散的无规行走问题本身早已经发展成一个活跃的研究领域。最简单的等步长的无规行走问题,除了〈xn〉=0,〈xn2〉∝n,还有一个重要特征量:从原点出发再次返回原点的概率。它与空间维数有关。一维行走返回原点的概率为1;二维行走返回原点的概率也是1;但三维行走返回原点的概率小于1,仅为 0.3405373296…
纯无规行走对于走过的点没有记忆。非随机性表现为对历史的某种记忆。可以考察〈xn2〉同n的关系,来判断所研究的过程偏离完全随机的程度。如果走过的点都不许再碰,称为自回避行走(英文缩写是SAW)。这是对溶液中高分子链的很好描述。一种二维的、只是第一步不许返回的无规行走问题导致统计物理学中著名的二维伊辛(Ising)模型的严格解,但相应的三维推广只给出一个封闭的高温近似解。[1]
试问平面中n步正向SAW有多少种?这个种类数m是没有封闭解但存在具体答案的计数问题的实例:
这是《整数序列全书》[2]中的第A046170号序列。
我们再看一个无规行走的“现代”应用:DNA行走。
对很长的由4个字母组成的DNA序列,令A、C、G、T对应上下左右4个方向。从2维格子的原点和序列的最左端出发,每见到一个字母移动一格。这不是随机行走,因为每个序列对应一个特定的实现,不能随机重复和取平均值。然而,可以随着n增加,问行走n步之后,到原点的距离rn的平均值和平方平均值如何随n变化?自然,〈rn〉=0,但〈rn2〉∝nα中的指数α是大于、小于还是等于1/2?
1992年发表在英国《自然》杂志上的一篇文章[3]考察了一维的DNA行走,即只区分两个左右方向:遇嘌呤(A或G)向左一步、遇嘧啶(C或T)向右一步。他们的结论是α>1/2,而且编码段比非编码段更随机。这篇文章引起了几百篇后继论文,正反参半。
4
爱因斯坦并没有因为布朗运动理论而得到诺贝尔奖,但法国物理学家皮兰(Jean Baptiste Perrin,1870—1942)却因为1908年以来证实爱因斯坦理论的实验研究获得1926年的诺贝尔物理学奖。获奖说明是“为了他关于物质离散结构特别是沉积平衡的发现”。
当时布朗运动实验的主要意义在于它证明了分子存在,并且提供了测量阿佛伽德罗常数的一种新办法。沉积平衡的直观实例发生在超速离心机中。高速旋转的处于水平位置的试管里,大小不同的颗粒在离心力作用下沿径向往外运动,越往外离心力也越大,但所受到的液体的黏滞阻力也越大,于是在一定半径处达到平衡。这是现代分子生物学实验室里分离大小分子集团的重要手段之一。由沉积平衡定义的沉积系数S,在分子生物学中作为分子量的度量一直沿用至今。例如,23S rRNA确实比16S rRNA大,但并不成简单比例关系。
有趣的是同年的诺贝尔化学奖颁给了瑞典人斯维德堡(Theodor Svedberg,1884—1971),理由是“为了他关于弥散系统的工作”,而斯维德堡的诺贝尔演讲题目却是“超速离心机”。沉降系数S又称斯维德堡单位,并没有因为皮兰而改用P。
5
法国物理学家朗之万(Paul Langevin,1872—1946)是中国物理学界的朋友。他在1931年作为国际物理学联合会的代表来到当时的北平,协助建立了中国物理学会,并且当选为中国物理学会的第一位外籍会员。他是我国声学前辈汪德昭先生的老师。朗之万晚年成为法国共产党人和反法西斯抵抗运动的斗士。
爱因斯坦用统计物理和流体力学方法,考察多个布朗粒子的分布,导出了扩散长度公式。朗之万在1908年为单个粒子写出“随机力”F(t)作用下的“牛顿方程”:
这是历史上第一个随机微分方程。我们先不把随机力F(t)具体化,直接对线性的朗之万方程求积分:
很自然地假定:
朗之万方程肇始了整个随机微分方程的数学理论。我们主要沿三条线对后来的发展稍作说明:
(1)朗之万方程的各种推广:广义朗之万方程;
(2)决定朗之万随机变量分布函数的方程:福克—普朗克方程;
(3)朗之万解空间上的连续积分。
6
线性的朗之万方程后来结合各种应用被大踏步地推广。广义朗之万方程可以写成:
对随机力做高斯分布假定:
7
其实,出现在线性的朗之万方程或广义朗之万方程中的两个常数,摩擦系数k和涨落力的关联强度D(或前面σij的对称部分)并不能随便给定。它们的关系要由“终值条件”决定:时间无穷长时,布朗粒子要与所处环境达到热平衡,也遵从能量均分定理。联系这两个量的关系因而含有温度T。这个关系式也出现在爱因斯坦1905年的论文中。这是涨落耗散定理的一个实例。涨落耗散定理的另一个早期实例是电路中电流噪声和电阻的关系。这两个例子代表着两类涨落耗散定理。线性输运过程框架内的涨落耗散定理的一般理论,是在20世纪50年代建立的。
涨落耗散定理是接近平衡态的非平衡理论的重要内容。接近平衡但又处于不平衡的系统中有三种最基本的过程,这就是趋向平衡、线性输运和涨落。这三种过程本质上密切相关。假定液体中某处的溶质浓度忽然比附近增高,因而局部偏离平衡,那下一时刻就会产生粒子流使得多余的溶质向浓度低的方向扩散。扩散流比例于浓度梯度。扩散引起耗散,不过耗散是比例于扩散流的平方的二阶效应。无论局部的浓度增加是由于从外界注入溶质,还是来自内部涨落,随后发生的扩散过程是一样的。这是涨落耗散定理的物理基础。
微分方程的初值问题在物理学中处理简单问题时比比皆是、司空见惯。涨落耗散定理出现在求解朗之万方程所加的终值条件中。我们在讨论布朗运动这样的复杂现象时常常遇到“终值条件”。生物学家们描述更复杂的生命现象时有时使用“目的论”(teleology)的语言就更不足为奇了。
8
既然提到了线性输运过程,我们就再说几句,以便后面讲到涨落场论特别是其非线性推广时,有所对比。
首先是广义力和广义流的概念。电位差导致电流,浓度差导致扩散流,温度差导致热流,等等。可以定义广义势V,它的势差给出广义力Fi,而广义力导致广义流Ji。这是“对角项”。还可以存在非对角的交叉项:电位差可以导致热流,温度差可以引起电流,等等。在线性范围内可以写成。
9
其实,前面依据物理直观写出的朗之万方程或广义朗之万方程,在数学上很成问题。随机项使得它们的解可能变得无界,所涉及的导数也可能不存在。由此在随机微分方程理论中引出来整个新篇章,如所谓伊藤清(ItÔ)算法和Stratonovich算法,它们在数学上等价,但数值计算时的方便程度不同。我们不去涉足这些数学理论,只指出朗之万方程的一种研究得比较好的极限情况,是定常、高斯、马可夫和连续概率分布条件下的随机过程,即欧尔斯坦-乌伦别克(OU)过程。
我们不进入OU过程的理论本身,而只借此提及非平衡统计理论中几代人的故事。欧尔斯坦(L.S.Orstein,1880—1941)同乌伦别克(George E.Uhlenbecd,1900—1988)在1930年撰写的综述[4]是爱因斯坦最初文章之后25年布朗运动理论的总结,又过了15年乌伦别克和他的中国女学生王明贞(1906—)又撰写了综述的第二部分[5]。这两篇文章至今是钻研经典布朗运动理论的入门必读。今年99岁高龄的王明贞女士是清华大学的退休教授。
乌伦别克的另一位中国女学生是已故的王承书(1912—1994)院士。她在流体力学基本方程的统计推导和高阶声波的研究方面有过重要贡献。
10
朗之万方程可以看成从随机变量x(t)向随机变量v(t)的变换关系。假定随机变量x的初始分布函数为
从每个朗之万方程可以推导出一个福克-普朗克方程,而每个福克-普朗克方程对应无穷多个朗之万方程。这是因为无穷多组随机变量可以遵从同一种概率分布,它们是随机等价的。随机等价与规范场理论中的规范等价有一些相似性。如果从技术上追究这种多值性的原因,则它源于矩阵开方的多值性。
如果福克-普朗克方程的解不随时间变化,即¶P/¶t = 0,则这是一个定态解。漂移系数Ki和扩散系数Dij必须满足一定条件,才能保证存在定态解,而且这个定态解可以通过位势函数V表示:Pµe-V/kT。这就是“位势条件”。冯·坎本(von Kampen)在1958年,哈肯(H. Haken)等在1970年代都研究过位势条件。位势条件的背后是细致平衡原理,细致平衡原理的基础是时间反演不变性。因此,位势条件不仅适用于满足细致平衡原理的近平衡态,还适用于某些远离平衡的非平衡定态。
如果在福克-普朗克方程中把时间t换成“虚”时间it(作一个“维克旋转”),就得到形式上与量子力学中薛定谔方程结构类似的方程。理论物理研究所郑伟谋曾利用此种联系,前后为福克-普朗克方程和薛定谔方程各找到一组包含双阱位势的严格解。
11
朗之万方程的解依赖于随机变量的分布,因而不是一条轨道,而是无穷多条轨道的集合:
令相临时刻之差ti+1-ti = Î足够大,以致前后两点独立,每点遵从高斯分布。整个轨道是许多个独立分布的联合分布:
量子场论中的费曼连续积分出现于1948年,那是拉格朗日形式的积分。相应的哈密顿形式的连续积分,到1959年才由顾茨维勒(M. C. Gutzwiller)引入。
维纳的连续积分是哈密顿形式的。拉格朗日形式的维纳连续积分直到1953年才出现。这就是对应线性朗之万方程的昂萨格-马克乐普(Machlup)泛函。它的非线性推广,导致与量子场论高度并行的涨落场论。
12
布朗粒子所受到的磨擦力和随机力都来自“环境”。包含无穷自由度的环境没有精确的描述方式,它的一种模型是无穷多个谐振子组成的“热浴”。正是对环境的热平衡假定把温度引进了涨落耗散定理的表述。1960年代以后,激光的发展把量子噪声的研究提上了日程。量子耗散的描述也同热浴相关。这就促进了量子布朗运动理论的发展和量子涨落耗散定理的证明。纳米结构中粒子的运动更使得量子涨落和统计涨落必须同时研究。
布朗运动是一种无规的“永动”。正是对宏观系统和无穷长时间大量粒子运动的完全随机的假定,避免了布朗运动理论和热力学第二定律的矛盾。然而在纳米结构和小时间尺度下,对热力学第二定律的偏离也成为可以检验的事实。量子布朗粒子和热浴量子态纠缠,成为“退相干”的原因之一。这是量子计算和量子通信必须面对的困难。这一切使量子布朗运动成为1990年代以来的前沿研究课题。量子朗之万方程和量子连续积分的理论都有所发展。
13
像玻璃或“自旋玻璃”这样的无序固体是不同于晶体的一大类物质。它们的理论研究自然地和随机过程有密切联系。另一方面,许多优化和识别问题导致在极其复杂的高维的“能量”地形图中寻求最大或最小值,就像是为自旋玻璃寻找能量最小的基态。这类问题不可能用穷举或比较一切情况来获取答案,因为其计算量超过任何现在和未来的计算机的承受能力。较为有效的办法是设计适当的随机过程,来探索地形分布。随机模拟因而成为重要的计算方法,这里要用到布朗运动理论武库中的许多工具和概念。
14
我们用一种极为简单但并不严格的方法,引入对应广义朗之万方程的涨落场论。“一生二、二生三、三生万物”。可以从“1的分解”推导出一切
先把普通的一维d 函数
利用泛函d 函数的积分定义:
就使归一条件Zx[0,0]=1成为依赖于随机过程 的生成泛函:
15
Martin、Siggia和Rose三人在1973年为经典的流体力学基本方程组即Navier-Stokes方程写出变分原理。对于简单流体,一共有5个场量fi, =1,…,5。然而,还必须引入5个同fi不对易的共扼场,才能使得相应的Euler-Lagrange方程就是原来的流体力学方程组。
后来知道,MSR的共扼场相当于切矢场¶ /¶f。换言之,不能只用基底空间,还必须把切空间引进来。非线性动力学中求李亚彭诺夫指数也是切空间中的计算。
MSR场论当时的主要贡献是把克莱奇南(R.H.Kraichnan)用类似费曼图的办法对湍流做微扰描述时高阶图的数目弄清楚。直到最近还有人把MSR场论继续用于湍流研究。周光召等发展的统一描述平衡和非平衡现象的闭路格林函数理论[6,7],则更便于用拉格朗日形式的随机泛函论证MSR场论,使其与维纳连续积分更为接近。
16
在涨落场论中场量是对称性和守恒性的携带者,而物理量是复合算子的平均值。场量本身并不出现在最后的物理结果中。这在闭路格林函数的理论框架[6,7]中看得很清楚。所谓“闭路”是指时间轴从负无穷大发展到正无穷大,再回到负无穷大。由于正负时间支的选取,每个N点费曼图都是对应2N个积分。任何多点格林函数都有三套,一套用于同量子场论高度平行的理论表示,一套用于实际计算,一套用于表示最终需要的物理理。三套格林函数之间存在明确定义的变换。
闭路格林函数方法用于动态临界现象的分析,直接导致原来用广义朗之万方程实现的各种模型[6,7]。从这一理论自然看出,前面提到的模模偶合项乃是量子场论中熟知的Ward-Takahashi恒等式,是对称性的后果。模模偶合项的此种本质,后来被许多作者在不同的问题中重新发现过。
非平衡现象的各种较为普遍的数学表述,都有一个共同特点,那就是已经无穷多的自由度还要“双倍化”:闭路格林函数方法中的正负时间支,MSR场论中的基本场和共扼场,普里高津(I.Prigogine)理论中的超算子所作用的超空间,都是这样。目前还没有对此问题的一般性分析。
17
规范场量子化时对辅助场的连续积分,导致法捷耶夫-波波夫(Faddeev-Popov)“鬼”,它们会违反自旋和统计关系,带来一些理论困难。意大利理论物理学家帕里西(G.
18
布朗运动理论最新、最积极的应用,可能在于对细胞中各种分子“机器”作用原理的认识。
布朗粒子从极小时间尺度上的无规涨落获取能量,实现各种较大尺度上的无规运动,斯莫鲁霍夫斯基早在1912年就考虑过能否利用布朗运动实现定向运动的问题。费曼(R. Feynman)在1963年提出的“棘齿和棘爪”(ratchet and pawl)模型,原则上可以从两个不同的热浴获得能量,缓慢地做定向机械功。这是一种布朗马达。
细胞中有各种高效地把化学能转变为机械功的分子马达。例如,生物化学过程所需能量存储在称为“腺三磷”(三磷酸腺苷即ATP)的小分子的三磷酸键中,ATP贡献能量后成为ADP(腺二磷),需要重新“充电”成ATP。实现充电的蛋白质机器ATP合成酶,真是具有转动部分的小机器。还有许多长着蛋白质双脚或单腿的小膜泡,沿细胞骨架行走以输送各种物质,这些是线性分子马达。许多人尝试用布朗马达来解释分子马达。小分子在微观涨落上“冲浪”,它们以极高效率消耗能量,并不违反热力学定律。本书中欧阳钟灿的文章会继续介绍布朗运动理论与生物学有关的最新发展。
其实,从广义上讲,达尔文的进化论就是描述随机突变背景上的定向演化。可以参看英国《自然》杂志的一篇题为“达尔文马达”的短文[9]。
*
对液体中小悬浮无规运动的研究,1905年以前主要是实验观察、积累事实,逐步形成基本认识。从1905年到1950,理论和实验的重心在于证明原子和分子的存在。这一时期布朗运动理论成为非平衡态统计物理的重要组成部分、也成为随机微分方程和随机过程理论的试金石。从1950到1990,是涨落场论的形成阶段,这一理论的广泛应用尚有待开拓。1990年代以来,量子布朗运动理论进一步发展,对纳米结构中粒子运动和生物细胞中分子机器的认识可能成为布朗运动理论最重要和最富于建设性的应用。
在结束本文之前,我们把布朗运动理论放在更一般的背景上。现代数理科学描述自然界,有三种基本的“逼近”模式:周期、随机和混沌。周期模式以二体问题为典范,可以从刻普勒行星运动三定律、牛顿力学、狭义和广义相对论、从玻尔到狄拉克的氢原子模型,一直研究到杨氏对称关系(Yangian)。混沌模式以一维非线性映射为可解实例,横跨尺度变换下的不变性、标度律、对称破缺、临界指数、符号动力学、分形与分维,乃至重正化群等重要概念。随机模式以布朗运动为试金石,涉及本文提到和没有提到的方方面面。目前在我国数理和工程科学的高等教育中,对后两种模式还没有给予充分注意。愿这篇短文能起到一点促进作用。
[2]
[3]
[4]
[5]
[6]
[7]
[8]
[9]
作者简介
郝柏林,复旦大学理论生命科学研究中心,中国科学院理论物理研究所,院士。
1
英国植物学家罗伯特·布朗在1828年和1829年的《哲学》杂志上发表了两篇文章,描述自己在1927年夏天在显微镜下观察到花粉颗粒在液体中的不停顿的运动。他最初曾经以为是看到了生命运动,但后来确认这种运动对细小的有机和无机颗粒都存在,因而不是生命现象所致。布朗认为运动的原因在于这些颗粒包含着“活性分子”(active molecules),而与所处液体没有关系。事实上,布朗并不是观察到这类运动的第一人。他在上述两篇文章里就曾提到了约十位前人,包括做过大量观察的制作显微镜的巧手列文胡克(Antonnie von Leeuwenhock)。
2
爱因斯坦在1901—1905年期间致力于博士论文研究。他1905年发表的头一篇文章——“分子大小的新测定”就基于其博士论文。爱因斯坦考察了液体中悬浮粒子对渗透压的贡献,把流体力学方法和扩散理论结合起来,建议了测量分子尺寸和阿佛伽德罗常数的新办法。这样的研究同布朗运动发生关系是很自然的。然而,他1905年5月撰写的第二篇论文的题目并没有提及布朗运动。这篇题为《热的分子运动论所要求的静止液体中悬浮小粒子的运动》的文章,一开始就说:“可能,这里所讨论的运动就是所谓的布朗分子运动;可是,关于后者我所能得到唯一的资料是如此的不准确,以致在这个问题上我无法形成判断。”爱因斯坦确实建立了布朗运动的分子理论,并且开启了借助随机过程描述自然现象的数理科学发展方向。
我们不在此重复爱因斯坦当年对扩散系数D的推导,直接从熟知的(一维)扩散方程出发:
〈x〉=0,〈x2〉=2Dt
于是得到扩散长度的公式:
3
如果把时间离散化为步长Δt的小段,令t=nΔt,同时保持Δt适当的大,使得每小段时间头尾的运动彼此无关,于是行走n步的结果xn就是n个独立随机变量之和。自然:
〈xn〉=0,〈xn2〉∝n
可见,均方距离并不比例于步数n,而是:
∝
这里的1/2幂次出现在高分子构象统计等许多涉及随机运动的理论中。离散的无规行走问题本身早已经发展成一个活跃的研究领域。最简单的等步长的无规行走问题,除了〈xn〉=0,〈xn2〉∝n,还有一个重要特征量:从原点出发再次返回原点的概率。它与空间维数有关。一维行走返回原点的概率为1;二维行走返回原点的概率也是1;但三维行走返回原点的概率小于1,仅为 0.3405373296…
纯无规行走对于走过的点没有记忆。非随机性表现为对历史的某种记忆。可以考察〈xn2〉同n的关系,来判断所研究的过程偏离完全随机的程度。如果走过的点都不许再碰,称为自回避行走(英文缩写是SAW)。这是对溶液中高分子链的很好描述。一种二维的、只是第一步不许返回的无规行走问题导致统计物理学中著名的二维伊辛(Ising)模型的严格解,但相应的三维推广只给出一个封闭的高温近似解。[1]
试问平面中n步正向SAW有多少种?这个种类数m是没有封闭解但存在具体答案的计数问题的实例:
| n | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | … |
| m | 1 | 2 | 5 | 12 | 30 | 73 | 183 | 456 | 1151 | … |
我们再看一个无规行走的“现代”应用:DNA行走。
对很长的由4个字母组成的DNA序列,令A、C、G、T对应上下左右4个方向。从2维格子的原点和序列的最左端出发,每见到一个字母移动一格。这不是随机行走,因为每个序列对应一个特定的实现,不能随机重复和取平均值。然而,可以随着n增加,问行走n步之后,到原点的距离rn的平均值和平方平均值如何随n变化?自然,〈rn〉=0,但〈rn2〉∝nα中的指数α是大于、小于还是等于1/2?
1992年发表在英国《自然》杂志上的一篇文章[3]考察了一维的DNA行走,即只区分两个左右方向:遇嘌呤(A或G)向左一步、遇嘧啶(C或T)向右一步。他们的结论是α>1/2,而且编码段比非编码段更随机。这篇文章引起了几百篇后继论文,正反参半。
4
爱因斯坦并没有因为布朗运动理论而得到诺贝尔奖,但法国物理学家皮兰(Jean Baptiste Perrin,1870—1942)却因为1908年以来证实爱因斯坦理论的实验研究获得1926年的诺贝尔物理学奖。获奖说明是“为了他关于物质离散结构特别是沉积平衡的发现”。当时布朗运动实验的主要意义在于它证明了分子存在,并且提供了测量阿佛伽德罗常数的一种新办法。沉积平衡的直观实例发生在超速离心机中。高速旋转的处于水平位置的试管里,大小不同的颗粒在离心力作用下沿径向往外运动,越往外离心力也越大,但所受到的液体的黏滞阻力也越大,于是在一定半径处达到平衡。这是现代分子生物学实验室里分离大小分子集团的重要手段之一。由沉积平衡定义的沉积系数S,在分子生物学中作为分子量的度量一直沿用至今。例如,23S rRNA确实比16S rRNA大,但并不成简单比例关系。
有趣的是同年的诺贝尔化学奖颁给了瑞典人斯维德堡(Theodor Svedberg,1884—1971),理由是“为了他关于弥散系统的工作”,而斯维德堡的诺贝尔演讲题目却是“超速离心机”。沉降系数S又称斯维德堡单位,并没有因为皮兰而改用P。
5
法国物理学家朗之万(Paul Langevin,1872—1946)是中国物理学界的朋友。他在1931年作为国际物理学联合会的代表来到当时的北平,协助建立了中国物理学会,并且当选为中国物理学会的第一位外籍会员。他是我国声学前辈汪德昭先生的老师。朗之万晚年成为法国共产党人和反法西斯抵抗运动的斗士。爱因斯坦用统计物理和流体力学方法,考察多个布朗粒子的分布,导出了扩散长度公式。朗之万在1908年为单个粒子写出“随机力”F(t)作用下的“牛顿方程”:
这是历史上第一个随机微分方程。我们先不把随机力F(t)具体化,直接对线性的朗之万方程求积分:
很自然地假定:
朗之万方程肇始了整个随机微分方程的数学理论。我们主要沿三条线对后来的发展稍作说明:
(1)朗之万方程的各种推广:广义朗之万方程;
(2)决定朗之万随机变量分布函数的方程:福克—普朗克方程;
(3)朗之万解空间上的连续积分。
6
线性的朗之万方程后来结合各种应用被大踏步地推广。广义朗之万方程可以写成:对随机力做高斯分布假定:
7
其实,出现在线性的朗之万方程或广义朗之万方程中的两个常数,摩擦系数k和涨落力的关联强度D(或前面σij的对称部分)并不能随便给定。它们的关系要由“终值条件”决定:时间无穷长时,布朗粒子要与所处环境达到热平衡,也遵从能量均分定理。联系这两个量的关系因而含有温度T。这个关系式也出现在爱因斯坦1905年的论文中。这是涨落耗散定理的一个实例。涨落耗散定理的另一个早期实例是电路中电流噪声和电阻的关系。这两个例子代表着两类涨落耗散定理。线性输运过程框架内的涨落耗散定理的一般理论,是在20世纪50年代建立的。涨落耗散定理是接近平衡态的非平衡理论的重要内容。接近平衡但又处于不平衡的系统中有三种最基本的过程,这就是趋向平衡、线性输运和涨落。这三种过程本质上密切相关。假定液体中某处的溶质浓度忽然比附近增高,因而局部偏离平衡,那下一时刻就会产生粒子流使得多余的溶质向浓度低的方向扩散。扩散流比例于浓度梯度。扩散引起耗散,不过耗散是比例于扩散流的平方的二阶效应。无论局部的浓度增加是由于从外界注入溶质,还是来自内部涨落,随后发生的扩散过程是一样的。这是涨落耗散定理的物理基础。
微分方程的初值问题在物理学中处理简单问题时比比皆是、司空见惯。涨落耗散定理出现在求解朗之万方程所加的终值条件中。我们在讨论布朗运动这样的复杂现象时常常遇到“终值条件”。生物学家们描述更复杂的生命现象时有时使用“目的论”(teleology)的语言就更不足为奇了。
8
既然提到了线性输运过程,我们就再说几句,以便后面讲到涨落场论特别是其非线性推广时,有所对比。首先是广义力和广义流的概念。电位差导致电流,浓度差导致扩散流,温度差导致热流,等等。可以定义广义势V,它的势差给出广义力Fi,而广义力导致广义流Ji。这是“对角项”。还可以存在非对角的交叉项:电位差可以导致热流,温度差可以引起电流,等等。在线性范围内可以写成。
9
其实,前面依据物理直观写出的朗之万方程或广义朗之万方程,在数学上很成问题。随机项使得它们的解可能变得无界,所涉及的导数也可能不存在。由此在随机微分方程理论中引出来整个新篇章,如所谓伊藤清(ItÔ)算法和Stratonovich算法,它们在数学上等价,但数值计算时的方便程度不同。我们不去涉足这些数学理论,只指出朗之万方程的一种研究得比较好的极限情况,是定常、高斯、马可夫和连续概率分布条件下的随机过程,即欧尔斯坦-乌伦别克(OU)过程。我们不进入OU过程的理论本身,而只借此提及非平衡统计理论中几代人的故事。欧尔斯坦(L.S.Orstein,1880—1941)同乌伦别克(George E.Uhlenbecd,1900—1988)在1930年撰写的综述[4]是爱因斯坦最初文章之后25年布朗运动理论的总结,又过了15年乌伦别克和他的中国女学生王明贞(1906—)又撰写了综述的第二部分[5]。这两篇文章至今是钻研经典布朗运动理论的入门必读。今年99岁高龄的王明贞女士是清华大学的退休教授。
乌伦别克的另一位中国女学生是已故的王承书(1912—1994)院士。她在流体力学基本方程的统计推导和高阶声波的研究方面有过重要贡献。
10
朗之万方程可以看成从随机变量x(t)向随机变量v(t)的变换关系。假定随机变量x的初始分布函数为从每个朗之万方程可以推导出一个福克-普朗克方程,而每个福克-普朗克方程对应无穷多个朗之万方程。这是因为无穷多组随机变量可以遵从同一种概率分布,它们是随机等价的。随机等价与规范场理论中的规范等价有一些相似性。如果从技术上追究这种多值性的原因,则它源于矩阵开方的多值性。
如果福克-普朗克方程的解不随时间变化,即¶P/¶t = 0,则这是一个定态解。漂移系数Ki和扩散系数Dij必须满足一定条件,才能保证存在定态解,而且这个定态解可以通过位势函数V表示:Pµe-V/kT。这就是“位势条件”。冯·坎本(von Kampen)在1958年,哈肯(H. Haken)等在1970年代都研究过位势条件。位势条件的背后是细致平衡原理,细致平衡原理的基础是时间反演不变性。因此,位势条件不仅适用于满足细致平衡原理的近平衡态,还适用于某些远离平衡的非平衡定态。
如果在福克-普朗克方程中把时间t换成“虚”时间it(作一个“维克旋转”),就得到形式上与量子力学中薛定谔方程结构类似的方程。理论物理研究所郑伟谋曾利用此种联系,前后为福克-普朗克方程和薛定谔方程各找到一组包含双阱位势的严格解。
11
朗之万方程的解依赖于随机变量的分布,因而不是一条轨道,而是无穷多条轨道的集合:令相临时刻之差ti+1-ti = Î足够大,以致前后两点独立,每点遵从高斯分布。整个轨道是许多个独立分布的联合分布:
量子场论中的费曼连续积分出现于1948年,那是拉格朗日形式的积分。相应的哈密顿形式的连续积分,到1959年才由顾茨维勒(M. C. Gutzwiller)引入。
维纳的连续积分是哈密顿形式的。拉格朗日形式的维纳连续积分直到1953年才出现。这就是对应线性朗之万方程的昂萨格-马克乐普(Machlup)泛函。它的非线性推广,导致与量子场论高度并行的涨落场论。
12
布朗粒子所受到的磨擦力和随机力都来自“环境”。包含无穷自由度的环境没有精确的描述方式,它的一种模型是无穷多个谐振子组成的“热浴”。正是对环境的热平衡假定把温度引进了涨落耗散定理的表述。1960年代以后,激光的发展把量子噪声的研究提上了日程。量子耗散的描述也同热浴相关。这就促进了量子布朗运动理论的发展和量子涨落耗散定理的证明。纳米结构中粒子的运动更使得量子涨落和统计涨落必须同时研究。布朗运动是一种无规的“永动”。正是对宏观系统和无穷长时间大量粒子运动的完全随机的假定,避免了布朗运动理论和热力学第二定律的矛盾。然而在纳米结构和小时间尺度下,对热力学第二定律的偏离也成为可以检验的事实。量子布朗粒子和热浴量子态纠缠,成为“退相干”的原因之一。这是量子计算和量子通信必须面对的困难。这一切使量子布朗运动成为1990年代以来的前沿研究课题。量子朗之万方程和量子连续积分的理论都有所发展。
13
像玻璃或“自旋玻璃”这样的无序固体是不同于晶体的一大类物质。它们的理论研究自然地和随机过程有密切联系。另一方面,许多优化和识别问题导致在极其复杂的高维的“能量”地形图中寻求最大或最小值,就像是为自旋玻璃寻找能量最小的基态。这类问题不可能用穷举或比较一切情况来获取答案,因为其计算量超过任何现在和未来的计算机的承受能力。较为有效的办法是设计适当的随机过程,来探索地形分布。随机模拟因而成为重要的计算方法,这里要用到布朗运动理论武库中的许多工具和概念。
14
我们用一种极为简单但并不严格的方法,引入对应广义朗之万方程的涨落场论。“一生二、二生三、三生万物”。可以从“1的分解”推导出一切先把普通的一维d 函数
利用泛函d 函数的积分定义:
就使归一条件Zx[0,0]=1成为依赖于随机过程 的生成泛函:
15
Martin、Siggia和Rose三人在1973年为经典的流体力学基本方程组即Navier-Stokes方程写出变分原理。对于简单流体,一共有5个场量fi, =1,…,5。然而,还必须引入5个同fi不对易的共扼场,才能使得相应的Euler-Lagrange方程就是原来的流体力学方程组。后来知道,MSR的共扼场相当于切矢场¶ /¶f。换言之,不能只用基底空间,还必须把切空间引进来。非线性动力学中求李亚彭诺夫指数也是切空间中的计算。
MSR场论当时的主要贡献是把克莱奇南(R.H.Kraichnan)用类似费曼图的办法对湍流做微扰描述时高阶图的数目弄清楚。直到最近还有人把MSR场论继续用于湍流研究。周光召等发展的统一描述平衡和非平衡现象的闭路格林函数理论[6,7],则更便于用拉格朗日形式的随机泛函论证MSR场论,使其与维纳连续积分更为接近。
16
在涨落场论中场量是对称性和守恒性的携带者,而物理量是复合算子的平均值。场量本身并不出现在最后的物理结果中。这在闭路格林函数的理论框架[6,7]中看得很清楚。所谓“闭路”是指时间轴从负无穷大发展到正无穷大,再回到负无穷大。由于正负时间支的选取,每个N点费曼图都是对应2N个积分。任何多点格林函数都有三套,一套用于同量子场论高度平行的理论表示,一套用于实际计算,一套用于表示最终需要的物理理。三套格林函数之间存在明确定义的变换。闭路格林函数方法用于动态临界现象的分析,直接导致原来用广义朗之万方程实现的各种模型[6,7]。从这一理论自然看出,前面提到的模模偶合项乃是量子场论中熟知的Ward-Takahashi恒等式,是对称性的后果。模模偶合项的此种本质,后来被许多作者在不同的问题中重新发现过。
非平衡现象的各种较为普遍的数学表述,都有一个共同特点,那就是已经无穷多的自由度还要“双倍化”:闭路格林函数方法中的正负时间支,MSR场论中的基本场和共扼场,普里高津(I.Prigogine)理论中的超算子所作用的超空间,都是这样。目前还没有对此问题的一般性分析。
17
规范场量子化时对辅助场的连续积分,导致法捷耶夫-波波夫(Faddeev-Popov)“鬼”,它们会违反自旋和统计关系,带来一些理论困难。意大利理论物理学家帕里西(G.
18
布朗运动理论最新、最积极的应用,可能在于对细胞中各种分子“机器”作用原理的认识。布朗粒子从极小时间尺度上的无规涨落获取能量,实现各种较大尺度上的无规运动,斯莫鲁霍夫斯基早在1912年就考虑过能否利用布朗运动实现定向运动的问题。费曼(R. Feynman)在1963年提出的“棘齿和棘爪”(ratchet and pawl)模型,原则上可以从两个不同的热浴获得能量,缓慢地做定向机械功。这是一种布朗马达。
细胞中有各种高效地把化学能转变为机械功的分子马达。例如,生物化学过程所需能量存储在称为“腺三磷”(三磷酸腺苷即ATP)的小分子的三磷酸键中,ATP贡献能量后成为ADP(腺二磷),需要重新“充电”成ATP。实现充电的蛋白质机器ATP合成酶,真是具有转动部分的小机器。还有许多长着蛋白质双脚或单腿的小膜泡,沿细胞骨架行走以输送各种物质,这些是线性分子马达。许多人尝试用布朗马达来解释分子马达。小分子在微观涨落上“冲浪”,它们以极高效率消耗能量,并不违反热力学定律。本书中欧阳钟灿的文章会继续介绍布朗运动理论与生物学有关的最新发展。
其实,从广义上讲,达尔文的进化论就是描述随机突变背景上的定向演化。可以参看英国《自然》杂志的一篇题为“达尔文马达”的短文[9]。
*
对液体中小悬浮无规运动的研究,1905年以前主要是实验观察、积累事实,逐步形成基本认识。从1905年到1950,理论和实验的重心在于证明原子和分子的存在。这一时期布朗运动理论成为非平衡态统计物理的重要组成部分、也成为随机微分方程和随机过程理论的试金石。从1950到1990,是涨落场论的形成阶段,这一理论的广泛应用尚有待开拓。1990年代以来,量子布朗运动理论进一步发展,对纳米结构中粒子运动和生物细胞中分子机器的认识可能成为布朗运动理论最重要和最富于建设性的应用。
在结束本文之前,我们把布朗运动理论放在更一般的背景上。现代数理科学描述自然界,有三种基本的“逼近”模式:周期、随机和混沌。周期模式以二体问题为典范,可以从刻普勒行星运动三定律、牛顿力学、狭义和广义相对论、从玻尔到狄拉克的氢原子模型,一直研究到杨氏对称关系(Yangian)。混沌模式以一维非线性映射为可解实例,横跨尺度变换下的不变性、标度律、对称破缺、临界指数、符号动力学、分形与分维,乃至重正化群等重要概念。随机模式以布朗运动为试金石,涉及本文提到和没有提到的方方面面。目前在我国数理和工程科学的高等教育中,对后两种模式还没有给予充分注意。愿这篇短文能起到一点促进作用。
参考文献
[1][2]
[3]
[4]
[5]
[6]
[7]
[8]
[9]
作者简介
郝柏林,复旦大学理论生命科学研究中心,中国科学院理论物理研究所,院士。


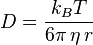





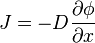

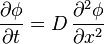
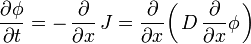



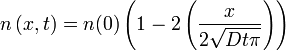

 為通量;
為通量; 為
為 為擴散的表面積大小;
為擴散的表面積大小; 為流動方向下
為流動方向下 到
到 )。
)。
No comments:
Post a Comment