w3.math.sinica.edu.tw/math_media/d371/37101.pdf
論最新的電影、運動, 那一類的事情。 如果要討論 ..... 階導數和二階導數, 就這樣, 然後還有複分析、 柯西積分。 基本上只要 .... 我入行的時候做非交換規範場論(non-.
Symmetry of second derivatives。根據Schwarz定理(也稱為克萊羅定理),當函數的二階導數連續在一個
這是Symmetry of second derivatives。根據Schwarz定理(也稱為克萊羅定理),當函數的二階導數連續在一個點,偏導數的交換點。
二阶导数的对称性- 维基百科,自由的百科全书
zh.wikipedia.org/wiki/二阶导数的对称性
轉為繁體網頁
轉為繁體網頁
什麼是一個例子,一個函數的混合偏導數[數學] \壓裂{\部分^ 2 ...
www.readingcabin.com/article/03abbce9785d5f4474d29268efacf80b/
衍生物(数学)最新熱門話題_Derivatives (mathematics)_第6 ...
www.readingcabin.com/topic/7631e6db2d73c2f3c8b8bb380c518cec/6/
數學真魅: 數學常用辭彙Glossary of Maths terms
aishuxue.blogspot.com/2012/01/glossary-of-maths-terms.html
[PDF]數學科常用英漢辭彙
www.edb.gov.hk/attachment/sc/curriculum.../glossary05112012.pdf
数学科常用英汉词汇_百度文库
wenku.baidu.com/view/48827f87b9d528ea81c779c8.html?re=view
新增網頁1 - 數學系
www.math.nthu.edu.tw/~hwang/mathnounn.htm
[DOC]A
www.hkedcity.net/citizen_files/aa/cb/kl5566/.../word_translation.doc
吳新謀,什麼是吳新謀,吳新謀釋義_華文詞源
www.43577.com/show/488333.shtml
[PDF]abacus 算盤absence 無,不存在absolute maximum 絕對極大 ...
cs.nju.edu.cn/wuxb/mathterms.pdf
二阶导数的对称性[编辑]
维基百科,自由的百科全书
数学中,二阶导数的对称性(也称为混合导数的相等)指取一个 n 元函数
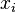 的偏导数用一个下标
的偏导数用一个下标 表示,则对称性断言二阶偏导数
表示,则对称性断言二阶偏导数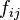 满足等式
满足等式
在最正常的情形黑塞矩阵实际上是对称矩阵;但从数学分析的观点来看这不是一个安全的论述,在特定一个点除了二阶导数的存在之外还需进一步的假设。克莱罗定理给出了关于 f 的一个充分条件使其成立。
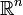 中任何一点
中任何一点 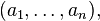 有连续二阶偏导数,则对
有连续二阶偏导数,则对 
 :
:
展示非對稱的一個例子如下:
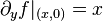 ,所以
,所以
 ,所以
,所以 。那就是说,在(0,0)处
。那就是说,在(0,0)处 ,尽管 f 的混合導數存在,且在
,尽管 f 的混合導數存在,且在 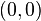 之外處處連續。注意到它與克莱罗定理并不矛盾,因為導數在 (0,0) 不連續。 一般地,極限運算的交換未必交換,兩個變量情形下,在 (0, 0) 附近考慮
之外處處連續。注意到它與克莱罗定理并不矛盾,因為導數在 (0,0) 不連續。 一般地,極限運算的交換未必交換,兩個變量情形下,在 (0, 0) 附近考慮
 。由于在这个例子中,黑塞矩阵在
。由于在这个例子中,黑塞矩阵在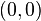 外所有点对称,Hessian矩阵看作施瓦茨分布是对称的事实,不存在矛盾。
外所有点对称,Hessian矩阵看作施瓦茨分布是对称的事实,不存在矛盾。
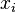 的偏导数用一个下标
的偏导数用一个下标 表示,则对称性断言二阶偏导数
表示,则对称性断言二阶偏导数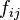 满足等式
满足等式黑塞矩阵是典型对称的[编辑]
f 的二阶偏导数称为 f 的黑塞矩阵。主对角线之外的元素是混合导数;即关于不同两个变量相继之导数。在最正常的情形黑塞矩阵实际上是对称矩阵;但从数学分析的观点来看这不是一个安全的论述,在特定一个点除了二阶导数的存在之外还需进一步的假设。克莱罗定理给出了关于 f 的一个充分条件使其成立。
对称性的正式表述[编辑]
用符号表示,对称性说,例如- Di . Dj = Dj . Di.
克莱罗定理[编辑]
在数学分析中,克莱罗定理(Clairaut's theorem)或施瓦兹定理(Schwarz's theorem)[1],以亚历克西·克莱罗与赫尔曼·施瓦兹命名,断言如果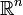 中任何一点
中任何一点 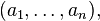 有连续二阶偏导数,则对
有连续二阶偏导数,则对 
克莱罗常数[编辑]
这个定理的一个副产品是克莱罗常数(Clairaut's constant,亦称卡罗拉公式或克莱罗参数),涉及球面大圆上一点的维度与方位角。一个特定大圆等于它在赤道处的方位角,或弧道路, :
:分布理论描述[编辑]
也可利用分布(distribution)理论回避有这种对称性的解析问题。首先任何函数的导数(假设可积)可以定义为一个分布。第二分部积分将对称性问题丢给测试函数,这是光滑的当然满足对称性。从而,在分布的意义下,对称性总满足。(另一个方法,若定义了函数的傅立叶变换,注意到在变换中偏导数成为更显然交换的乘法算子)。对称性的要求[编辑]
当函数不满足克莱洛定理的前提的时候,例如其导数不连续,则不存在对称性。展示非對稱的一個例子如下:
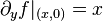 ,所以
,所以 ,所以
,所以 。那就是说,在(0,0)处
。那就是说,在(0,0)处 ,尽管 f 的混合導數存在,且在
,尽管 f 的混合導數存在,且在 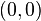 之外處處連續。注意到它與克莱罗定理并不矛盾,因為導數在 (0,0) 不連續。 一般地,極限運算的交換未必交換,兩個變量情形下,在 (0, 0) 附近考慮
之外處處連續。注意到它與克莱罗定理并不矛盾,因為導數在 (0,0) 不連續。 一般地,極限運算的交換未必交換,兩個變量情形下,在 (0, 0) 附近考慮 。由于在这个例子中,黑塞矩阵在
。由于在这个例子中,黑塞矩阵在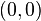 外所有点对称,Hessian矩阵看作施瓦茨分布是对称的事实,不存在矛盾。
外所有点对称,Hessian矩阵看作施瓦茨分布是对称的事实,不存在矛盾。李理论[编辑]
更高级的一个讨论是这样的:考虑一阶微分算子 Di 为欧几里得空间中的无穷小算子。即 Di 在某种意义下生成平行于 xi-轴平移的单参数群。显然这些群互相交换,从而我们希望无穷小生成元也交换;李括号- [Di, Dj] = 0


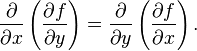

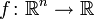
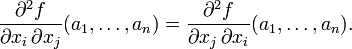


 在它的原点没有对称的二阶导数
在它的原点没有对称的二阶导数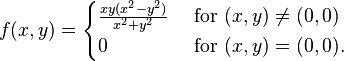


No comments:
Post a Comment