不過話說回來,講線性代數的書不一定會講到這個幾何意義,因為定義行列式幾行就寫完了,但是定義面積(體積),尤其是高維空間的面積(體積)是一件相當麻煩的事情。
如果讀者只讀過線性代數,那麽不妨這樣直觀感受一下行列式。而如果讀者讀過實變函數或者測度論,那麽這個結論可以作為一道不錯的習題。
时空中的变换群,若群参数为常数,则只是运动学意义上的变换群,对应运动学意义上的对称性
音乐快递:时空中的变换群,若群参数为常数,则只是运动学 ...
bbs.wenxuecity.com › 论坛 › 音乐快递 - 轉為繁體網頁
作者: 星空浩淼 时间: 2010-12-19 19:16 标题: 学习中遇到的疑问,请教sage兄和季候风兄
目前我每周都有几天时间系统地打一些基础,在学习过程中,时常会遇到一些疑问。
请教sage兄和季候风兄:
在广义相对论中,跟广义协变性对应的变换群,其独立的群参数一共有多少个(没有办法,我找不到文献解答,只好在这里求助了)?
我们知道,无挠的四维黎曼时空的曲率张量,最多有20个独立分量。曾经有人告诉我说,跟广义协变性对应的变换群,其独立的群参数一共有20个,我不知道这二者之间是否有什么关系。
如果仅仅从一组时空坐标变换到另一组时空坐标的表达式来看(仅仅要求变换矩阵可逆),这个4×4变换矩阵所构成的变换群,最多有16个独立参数。
[ 本帖最后由 星空浩淼 于 2010-12-20 10:19 编辑 ]
作者: 星空浩淼 时间: 2010-12-20 01:20
假定跟广义协变性对应的变换群,的确有20个独立参数,我自己是通过这样猜测来理解的,不知道对不对(没有办法,我实在找不到相关文献来提供标准答案):
1)我们知道,彭加勒群有10个独立参数,但它只是一个运动学意义上的群,如果要把广义相对论中的广义协变性包括进去,还要考虑有动力学内容的变换群(局域化的对称群)。
2)让彭加勒群的10个独立参数,都成为故有时的函数,这样,就还要考虑这10个独立参数对故有时τ的导数(比如取τ=0时的值)。这样,就有20个独立参数了,它们同时概括了运动学和动力学内容,后者和“惯性系与加速系之间的变换”有关。
3)如果把彭加勒群的10个独立参数看做广义坐标,则这10个独立参数对故有时的导数,相当于10个独立的广义速度(或者通过某个变换换成10个独立的广义动量)。如果是上述这样,那么把彭加勒群的10个独立参数看做广义坐标,再把它们对故有时的导数构造出对应的广义动量来,得到的20维群流形,就相当于20维的“辛流形”了。
此外,我的感受是:广义相对论的美,除了其原有的美,还有把它纳入nonAbel规范场的语言框架时所体现出来的美。把广义相对论纳入nonAbel规范场的语言框架时,需要把部分时空分量指标看作是不同场的编号指标,这样就得到联络1形式和曲率2形式,它们分别与规范势和场强张量相对应。在QCD中,不同场的编号指标是色指标(统称为“荷指标”),由于色荷与惯性质量是两回事,所以在这里,荷指标与时空分量指标是分开的。而引力场就不同,由于荷质量与惯性质量等价,所以表示不同场的编号指标(“荷指标”)同时也是时空分量指标。当然,这也可以换一个角度来说,与引力场对应的规范变换群,是时空空间中的变换群,所以“荷指标”同时也是时空分量指标;而QCD中的规范群是内部空间中的变换群,所以荷指标不同于时空分量指标。
[ 本帖最后由 星空浩淼 于 2010-12-22 01:33 编辑 ]
作者: 季候风 时间: 2010-12-21 04:56
群的所谓“独立参数” 是一个模糊的概念。
对于有限维李群,如果其李代数线性同构于![\mathbb R^n \mathbb R^n]() , 则我们说有 n 个独立参数。
, 则我们说有 n 个独立参数。
对于无限维李群,显然这个答案不是你想要的,因为有无穷个独立参数。
物理学家在这种情况下用 “独立参数” 指代函数。
对于微分同胚群,它的确有李代数,就是时空流形上的所有切矢量场组成的李代数。
如果流形比较复杂,这个李代数也许并不线性同构于任何函数空间。
但对于拓扑平凡的流形(![\mathbb R^4 \mathbb R^4]() ), 要指定一个切矢量场,只需要指定
), 要指定一个切矢量场,只需要指定
在自然基下的分量即可。所以这个李代数同构于![\big(C^\infty(\mathbb R^4) \big)^4 \big(C^\infty(\mathbb R^4) \big)^4]() ,
,
或者说,微分同胚群有四个 “独立参数”
作者: 星空浩淼 时间: 2010-12-21 09:57
谢谢季兄
物理学中群的“独立参数”,通常好像特指跟生成元一一对应的参数吧。例如,彭加勒群的10个独立参数是:
1)三维空间转动变换,有三个空间转动角,它们构成三个参数;
2)时间轴与空间轴之间的伪转动(即三个空间方向上的Lorentz boost),有三个伪转动角(即惯性系之间的、三个方向上的相对速度),它们构成三个参数;
3)四维时空平移变换x^μ→x^μ+a^μ,又有四个参数a^μ(μ=0,1,,2,3)。
换句话说,我是在上述含义下,想知道广义相对论中与广义协变性对应的群参数数量。当然,我们知道,规范场论中,从整体规范变换到局域规范变换,生成元个数没有变,相应的群参数的个数也就没有变。人们试图把广义相对论纳入规范场论的语言框架时,曾经以为对应的规范变换,就是局域化的彭加勒变换。但实际上又发现,广义相对论中涉及到的“规范变换”,要比局域化的彭加勒变换还要广泛,比如说,局域化的彭加勒变换还是10个独立的群参数,而广义相对论中涉及到的“规范变换”,有20个群参数。我想知道广义相对论中涉及到的“规范变换”,其群参数到底有多少个,它们具体对应哪些参数(其中应该包含彭加勒群的10个参数)
我在2楼,是在假定的确有20个独立参数的前提下,试图给出这20个参数一个等价的描述。在通常的描述中,也许不是象2楼这么说的,但本质上可以与2楼的描述等价起来。
[ 本帖最后由 星空浩淼 于 2010-12-21 11:13 编辑 ]
作者: Non 时间: 2010-12-21 21:09 标题: GL(4,R)
4-dimension symmetric General linear group GL(4,R), with 10 independent parameters. four parameters more than Lorentz group.
作者: 星空浩淼 时间: 2010-12-21 23:31 标题: 回复 5# 的帖子
既然如此,为何局域彭加勒变换,不能概括广义相对论中涉及到的任意可逆的坐标变换呢?人们都说,任意可逆的坐标变换群,要比局域的彭加勒群大(因而独立的群参数会更多),这正是令我迷惑的地方:我不知道这多出来的那些独立群参数,到底是哪些群参数?
作者: 季候风 时间: 2010-12-22 11:40
引力作为规范理论,只需要把平移局域化就够了。
作者: 星空浩淼 时间: 2010-12-22 18:08 标题: 回复 7# 的帖子
由于引力荷是能量动量张量,而能量动量张量是时空平移不变时的Noether荷,因此很多人一开始都以为引力对应的规范场论,其规范变换只是时空平移变换,但很快发现不是这样。最起码,还要包含局域的Lorentz变换。即使是局域的彭加勒变换,都无法概括与引力相关的全部规范变换。
作者: 季候风 时间: 2010-12-22 21:29
任何变换都能写成局域平移变换:
![x'_\mu = f_\mu (x) = x_\mu + (f_\mu(x)-x_\mu) x'_\mu = f_\mu (x) = x_\mu + (f_\mu(x)-x_\mu)]()
令![a_\mu(x) = f_\mu(x) - x_\mu a_\mu(x) = f_\mu(x) - x_\mu]()
则![x'_\mu = x_\mu + a_\mu(x) x'_\mu = x_\mu + a_\mu(x)]()
作者: 星空浩淼 时间: 2010-12-23 00:43 标题: 回复 9# 的帖子
我去年这个时候,在昌海兄的主页上也表达过你的这个看法,但是无人回应
我发这栋楼的帖子,就是想弄明白,这一切的一切,到底是怎么回事。
上周我兴冲冲地跟别人讨论我的一个idea,结果人家说,这就是暗能量啊(我以前只知道暗能量这个名词)!
这么说,如果我从一开始就学物理搞物理,可能十几年前就给出“暗能量”的预言了![]() 因为如果那样的话,我会十几年前就开始正式学广义相对论。
因为如果那样的话,我会十几年前就开始正式学广义相对论。
我从去年这个时候开始系统学广义相对论,但是每次到了来年开学,又会停下来,因为我只有年底才有时间做自己想做的事情。
[ 本帖最后由 星空浩淼 于 2010-12-23 00:45 编辑 ]
作者: 季候风 时间: 2010-12-23 03:35
那你现在打算相信谁?
我已经给出了一个数学上的理由和一个物理上的理由,说明答案是 4.
作者: 星空浩淼 时间: 2010-12-23 09:43 标题: 回复 11# 的帖子
我想是这样:
通常的规范场论中,规范变换无论是整体的还是局域的,都对应同样多的生成元。例如QCD中,SU(3)群的群参数,无论是常数(对应整体规范变换)、还是与时空坐标有关(对应局域规范变换),生成元都是8个。
而在引力理论中,整体时空平移变换只有4个生成元。如果把时空坐标的任何局域变换,都看作是局域的时空平移变换,那么一旦时空平移变换局域化了,生成元至少会变成10个。这一点跟以上不同。
我不知道是不是因为这个原因,人们还是没有把局域化的Lorentz变换等等,视作局域的时空平移变换。无论怎样,引力的规范场论,始终与其他的规范场论有所不同,也许这是因为,前者与时空空间中的变换群有关而后者与内部空间上的变换群有关,或者说对引力而言,荷与惯性质量合二为一;而对其他规范场,荷是荷,惯性质量是惯性质量。
这就是我想同时请教你和sage兄的原因,如果你们两个同时从数学和物理的角度,给出同样的答案,那我心里有谱了![]() 。
。
作者: 季候风 时间: 2010-12-23 22:01
再给一个理由:
广义相对论与规范理论的类比,在数学上相当于切丛与 “外在矢量丛” 的类比。
所谓 “外在向量丛”,就是在底流形坐标变换下,局部平凡化不变的丛。
(如果局部平凡化随着底流形坐标变换而变,则是 “张量丛” 或者 “旋量丛”。)
外在向量丛的规范变换是矩阵函数 (转移函数)![a_{ij}(x) a_{ij}(x)]() ,
,
比如, SU(3) 规范理论的转移函数就是 3*3 矩阵值函数,满足幺正条件和行列式条件,
所以是 8 个独立函数决定的。
切丛则不同,其转移函数(即规范变换)是 Jacobi 矩阵![(\partial x'_\mu/ \partial x_\nu) (x) (\partial x'_\mu/ \partial x_\nu) (x)]() ,
,
虽然含有 16 个函数,但它们来自于 4 个函数![x'_\mu = x'_\mu(x) x'_\mu = x'_\mu(x)]() 的偏导数,
的偏导数,
所以在泛函意义上它们不是独立的,而只有原来的 4 个函数是 “独立” 的。
作者: 星空浩淼 时间: 2010-12-24 09:45 标题: 回复 13# 的帖子
季兄能否把最后一段说得更清楚一点?这个地方我没有听明白,谢谢!
有多少个独立函数,跟有多少个独立的导函数,是不同的——函数与函数的导函数,是相互独立的。一个自由度变量,跟它的对某参数的导数,是两个独立的自由度变量。
作者: 季候风 时间: 2010-12-24 22:39
几个参(函)数 “独立” 的意思,就我的理解,就是它们可以任意取。
最简单的比如四个平移参数,互相之间没有关系,“独立”,不存在约束,所以可以任取四个常数做坐标平移。
而一个函数的偏导数之间就存在约束。比如四元函数的四个偏导数之间就不是独立的。
任取四个函数,当然不一定正好构成一个四元函数的四个偏导数。
所以说,在切丛的转移矩阵(Jacobi 矩阵)中,矩阵元不能任取,存在约束。
但是广义坐标变换中四个函数![x_\mu' =x_\mu'(x) x_\mu' =x_\mu'(x)]() 就是可以任取的,它们是独立参(函)数。
就是可以任取的,它们是独立参(函)数。
作者: faltings 时间: 2010-12-25 01:37 标题: 回复 15# 的帖子
不赞同,这儿的情况比frobenus定理包含的情况要大,不一定要可微。
矩阵就是对称的GL(4,R)
作者: sage 时间: 2010-12-25 03:20 标题: 回复 15# 的帖子
那我心里有谱了
=======================
For the peace of your mind, I completely agree with 季兄. I think he has explained it to you very well, I cannot do better. Let me just tell you some of my own ways of understanding it.
1) The standard statement is that general relativity is a gauge theory, gauging the space-time translation (Poincare).
To understand this statement, it is necessary to understand what do we mean by gauging a symmetry. Of course, we need to
start with a global symmetry of the system. At the same time, the very important consequence of gauging is the
introduction of new dynamics, new degrees of freedom (the gauge fields). We all know gauging U(1) E&M means that we must
introduce photon.
In this sense, it is easy to understand why Lorentz transformation is not being gauged. Starting with an inertia frame, Lorentz
boost will not introduce gravitational effect. However, to make equations covariant under Poincare, it is necessary to
introduce gravitational field.
2) Here is another way to count the number 4. Maxwell equation cannot fix all 4 components of the vector potential, because
the Maxwell equations are not independent. In fact, one relation (Bianchi) exist among them. Therefore, Maxwell equations will
leave one degree of freedom unfixed. We all know that this is the one gauge degree of freedom of U(1). Similarly, 10 Einstein
equations are not independent. Bianchi identities of the left-hand side means 4 degrees of freedom unfixed. And, we all know that
this is the 4 gauge degree of freedom of general relativity.
3) Here is my guess where the number 20 comes from. Einstein equations are in general 2nd order differential equations of g_munu.
In principle, the relevant physical quantities can be g_{munu} (10 d.o.f), first derivatives g_{munu,gamma} (40), secondary
derivatives g_{munu,alpha beta} (100). However, many of them can be transformed away by gauge transformations. Say I am doing a
general coordinate transformation, x->x'. The functions I can use (to transform g_munu is its derivatives) are (schematically,
and partial derivatives, of course) dx/dx' (16 of them), d^2 x/(dx'dx') (40 of them), d^3 x/(dx' dx' dx') (80 of them). Now the 10 of 16 dx/dx'
can be used to set g_{mu nu} to flat eta_munu. The rest of 6 belongs to Lorentz and rotation (which as we have discussed not relevant for
gravitational dynamics). Then we use the 40 d^2 x/dx'dx' to set all 1st derivatives g_{munu, gamma} to be zero. Then among the 100
2nd derivatives (g_{munu,alpha beta}), we can set 80 of them to zero by using 80 d^3x/(dx'dx'dx'). Therefore, there are 20 physical components
in Riemann tensor (can not be gauged away).
Most of what I said here is, of course, in Weinberg.
作者: 星空浩淼 时间: 2010-12-25 11:35
谢谢sage兄和季兄,这个问题,经过你们这么一讨论,我现在基本上有一点谱了![]()
虽然还是存在一些疑问,只有随着我知识的增长,逐渐自己弄明白
[ 本帖最后由 星空浩淼 于 2010-12-26 11:37 编辑 ]
作者: Non 时间: 2010-12-25 14:37 标题: As for the extra 4 parameters
The extra 4 parameters are responsible for "changing" length in 4-dimension, having nothing to do with Poincare transformation (translation). You know Lorentz transformation conserves the "length" in 4-D.
[ 本帖最后由 Non 于 2010-12-25 06:40 编辑 ]
作者: 星空浩淼 时间: 2010-12-28 00:07 标题: 回复 19# 的帖子
我明白你说的意思了,谢谢!
其实只要拿支笔在纸上写一写就明白了:
x^μ=a^(μν)y_ν+a^μ
只要不再有“保持线元长度不变”这个限制,a^(μν)就有16个,再加上四个a^μ,共20个参数
在无穷小局域变换下,可以统一地看作是局域时空平移变换
[ 本帖最后由 星空浩淼 于 2010-12-28 09:39 编辑 ]
作者: 季候风 时间: 2010-12-28 03:10 标题: 回复 20# 的帖子
问题是这20个参数为常数的变换有任何物理意义吗?
作者: 星空浩淼 时间: 2010-12-28 09:50 标题: 回复 21# 的帖子
一般而言,时空中的变换群,若群参数为常数,则只是运动学意义上的变换群,对应运动学意义上的对称性。但是,这里仍然包含有只在广义相对论中才有的非平凡性——其中包含让四维时空线元长度任意改变的变换,这是在整体的彭家勒群变换中所没有的。
如果仅仅只是想知道到底有哪20参数,这可以提供一个答案,如此而已。有意义的,当然是局域化的变换群,此时就正如你所说,所有无穷小的局域变换,都对应局域的时空平移变换(不过跟整体时空平移变换群不同,此时群参数还是20个)。
[ 本帖最后由 星空浩淼 于 2010-12-28 20:26 编辑 ]
作者: 季候风 时间: 2010-12-29 01:19
呵呵,钻一下牛角尖:与其把这个作为 “20个参数”的解释,还不如放弃“20个参数”这种说法,
因为这种解释本身非常误导,暗示引力是把整个庞加莱对称性局域化的结果,而这并不正确。
作者: 星空浩淼 时间: 2010-12-29 08:40 标题: 回复 23# 的帖子
我见过不少专业文献,那里的确是把局域化的庞加莱对称性群看作是引力规范场论的部分规范对称群(比庞加莱更广泛的一般线性群,才是引力规范场论的全部规范对称性群),但我不知道自己记忆是否有误。
也许,这是一种历史上的一种约定成俗吧![]()
[ 本帖最后由 星空浩淼 于 2010-12-29 09:41 编辑 ]
作者: sage 时间: 2010-12-29 12:14 标题: 回复 24# 的帖子
Do you have a reference?
If it is like you said, then the article you have seen is wrong. There is clear answer, not a matter of convention.
作者: 星空浩淼 时间: 2010-12-30 01:20 标题: 回复 25# 的帖子
我看的文献有点老(很可能过时了),比如80年代Mills有篇文章,综述规范场的基本思想。从此文中,Mills似乎表明,他给出non-Abel规范场,似乎是受启发于广义相对论对引力场的处理。今天的人却似乎颠倒了过来,用规范场的思想去解读广义相对论中的引力场。虽然一个涉及内部空间,一个涉及时空空间,从微分几何的角度来看,二者的确有着类似的数理逻辑,有着类似的思想框架。
Mills在这篇文章里,就提到即使是局域化的庞加莱群,也不能覆盖与引力相关的全部仿射变换群。同时他还说(大意):令人感到惊讶的是,能动张量是引力源,按照规范场论的逻辑框架,时空平移变换群应该就可以概括引力场的全部规范群,然后却发现事实并非如此。
在细节上,我不能保证有没有记忆错误。我看的是那篇文章的中文版,发表在国内80年代的《自然》杂志上
[ 本帖最后由 星空浩淼 于 2010-12-30 01:22 编辑 ]
整个真空弥漫这这种HIGGS场,而物质粒子的质量就是取决于它们与这个背景场的耦合大小。用个不是很准确的比方,这就像大鱼在水中游泳觉得惯性大,而小虾感觉惯性小,惯性大小就是质量。
目前我每周都有几天时间系统地打一些基础,在学习过程中,时常会遇到一些疑问。
请教sage兄和季候风兄:
在广义相对论中,跟广义协变性对应的变换群,其独立的群参数一共有多少个(没有办法,我找不到文献解答,只好在这里求助了)?
我们知道,无挠的四维黎曼时空的曲率张量,最多有20个独立分量。曾经有人告诉我说,跟广义协变性对应的变换群,其独立的群参数一共有20个,我不知道这二者之间是否有什么关系。
如果仅仅从一组时空坐标变换到另一组时空坐标的表达式来看(仅仅要求变换矩阵可逆),这个4×4变换矩阵所构成的变换群,最多有16个独立参数。
[ 本帖最后由 星空浩淼 于 2010-12-20 10:19 编辑 ]
作者: 星空浩淼 时间: 2010-12-20 01:20
假定跟广义协变性对应的变换群,的确有20个独立参数,我自己是通过这样猜测来理解的,不知道对不对(没有办法,我实在找不到相关文献来提供标准答案):
1)我们知道,彭加勒群有10个独立参数,但它只是一个运动学意义上的群,如果要把广义相对论中的广义协变性包括进去,还要考虑有动力学内容的变换群(局域化的对称群)。
2)让彭加勒群的10个独立参数,都成为故有时的函数,这样,就还要考虑这10个独立参数对故有时τ的导数(比如取τ=0时的值)。这样,就有20个独立参数了,它们同时概括了运动学和动力学内容,后者和“惯性系与加速系之间的变换”有关。
3)如果把彭加勒群的10个独立参数看做广义坐标,则这10个独立参数对故有时的导数,相当于10个独立的广义速度(或者通过某个变换换成10个独立的广义动量)。如果是上述这样,那么把彭加勒群的10个独立参数看做广义坐标,再把它们对故有时的导数构造出对应的广义动量来,得到的20维群流形,就相当于20维的“辛流形”了。
此外,我的感受是:广义相对论的美,除了其原有的美,还有把它纳入nonAbel规范场的语言框架时所体现出来的美。把广义相对论纳入nonAbel规范场的语言框架时,需要把部分时空分量指标看作是不同场的编号指标,这样就得到联络1形式和曲率2形式,它们分别与规范势和场强张量相对应。在QCD中,不同场的编号指标是色指标(统称为“荷指标”),由于色荷与惯性质量是两回事,所以在这里,荷指标与时空分量指标是分开的。而引力场就不同,由于荷质量与惯性质量等价,所以表示不同场的编号指标(“荷指标”)同时也是时空分量指标。当然,这也可以换一个角度来说,与引力场对应的规范变换群,是时空空间中的变换群,所以“荷指标”同时也是时空分量指标;而QCD中的规范群是内部空间中的变换群,所以荷指标不同于时空分量指标。
[ 本帖最后由 星空浩淼 于 2010-12-22 01:33 编辑 ]
作者: 季候风 时间: 2010-12-21 04:56
群的所谓“独立参数” 是一个模糊的概念。
对于有限维李群,如果其李代数线性同构于
对于无限维李群,显然这个答案不是你想要的,因为有无穷个独立参数。
物理学家在这种情况下用 “独立参数” 指代函数。
对于微分同胚群,它的确有李代数,就是时空流形上的所有切矢量场组成的李代数。
如果流形比较复杂,这个李代数也许并不线性同构于任何函数空间。
但对于拓扑平凡的流形(
在自然基下的分量即可。所以这个李代数同构于
或者说,微分同胚群有四个 “独立参数”
作者: 星空浩淼 时间: 2010-12-21 09:57
谢谢季兄
物理学中群的“独立参数”,通常好像特指跟生成元一一对应的参数吧。例如,彭加勒群的10个独立参数是:
1)三维空间转动变换,有三个空间转动角,它们构成三个参数;
2)时间轴与空间轴之间的伪转动(即三个空间方向上的Lorentz boost),有三个伪转动角(即惯性系之间的、三个方向上的相对速度),它们构成三个参数;
3)四维时空平移变换x^μ→x^μ+a^μ,又有四个参数a^μ(μ=0,1,,2,3)。
换句话说,我是在上述含义下,想知道广义相对论中与广义协变性对应的群参数数量。当然,我们知道,规范场论中,从整体规范变换到局域规范变换,生成元个数没有变,相应的群参数的个数也就没有变。人们试图把广义相对论纳入规范场论的语言框架时,曾经以为对应的规范变换,就是局域化的彭加勒变换。但实际上又发现,广义相对论中涉及到的“规范变换”,要比局域化的彭加勒变换还要广泛,比如说,局域化的彭加勒变换还是10个独立的群参数,而广义相对论中涉及到的“规范变换”,有20个群参数。我想知道广义相对论中涉及到的“规范变换”,其群参数到底有多少个,它们具体对应哪些参数(其中应该包含彭加勒群的10个参数)
我在2楼,是在假定的确有20个独立参数的前提下,试图给出这20个参数一个等价的描述。在通常的描述中,也许不是象2楼这么说的,但本质上可以与2楼的描述等价起来。
[ 本帖最后由 星空浩淼 于 2010-12-21 11:13 编辑 ]
作者: Non 时间: 2010-12-21 21:09 标题: GL(4,R)
4-dimension symmetric General linear group GL(4,R), with 10 independent parameters. four parameters more than Lorentz group.
作者: 星空浩淼 时间: 2010-12-21 23:31 标题: 回复 5# 的帖子
既然如此,为何局域彭加勒变换,不能概括广义相对论中涉及到的任意可逆的坐标变换呢?人们都说,任意可逆的坐标变换群,要比局域的彭加勒群大(因而独立的群参数会更多),这正是令我迷惑的地方:我不知道这多出来的那些独立群参数,到底是哪些群参数?
作者: 季候风 时间: 2010-12-22 11:40
引用:
原帖由 星空浩淼 于 2010-12-21 09:57 发表
谢谢季兄
物理学中群的“独立参数”,通常好像特指跟生成元一一对应的参数吧。例如,彭加勒群的10个独立参数是:
1)三维空间转动变换,有三个空间转动角,它们构成三个参数;
2)时间轴与空间轴之间的伪转动(即三个空间方向上的Lore ...
作者: 星空浩淼 时间: 2010-12-22 18:08 标题: 回复 7# 的帖子
由于引力荷是能量动量张量,而能量动量张量是时空平移不变时的Noether荷,因此很多人一开始都以为引力对应的规范场论,其规范变换只是时空平移变换,但很快发现不是这样。最起码,还要包含局域的Lorentz变换。即使是局域的彭加勒变换,都无法概括与引力相关的全部规范变换。
作者: 季候风 时间: 2010-12-22 21:29
任何变换都能写成局域平移变换:
令
则
作者: 星空浩淼 时间: 2010-12-23 00:43 标题: 回复 9# 的帖子
我去年这个时候,在昌海兄的主页上也表达过你的这个看法,但是无人回应
我发这栋楼的帖子,就是想弄明白,这一切的一切,到底是怎么回事。
上周我兴冲冲地跟别人讨论我的一个idea,结果人家说,这就是暗能量啊(我以前只知道暗能量这个名词)!
这么说,如果我从一开始就学物理搞物理,可能十几年前就给出“暗能量”的预言了
我从去年这个时候开始系统学广义相对论,但是每次到了来年开学,又会停下来,因为我只有年底才有时间做自己想做的事情。
[ 本帖最后由 星空浩淼 于 2010-12-23 00:45 编辑 ]
作者: 季候风 时间: 2010-12-23 03:35
那你现在打算相信谁?
我已经给出了一个数学上的理由和一个物理上的理由,说明答案是 4.
作者: 星空浩淼 时间: 2010-12-23 09:43 标题: 回复 11# 的帖子
我想是这样:
通常的规范场论中,规范变换无论是整体的还是局域的,都对应同样多的生成元。例如QCD中,SU(3)群的群参数,无论是常数(对应整体规范变换)、还是与时空坐标有关(对应局域规范变换),生成元都是8个。
而在引力理论中,整体时空平移变换只有4个生成元。如果把时空坐标的任何局域变换,都看作是局域的时空平移变换,那么一旦时空平移变换局域化了,生成元至少会变成10个。这一点跟以上不同。
我不知道是不是因为这个原因,人们还是没有把局域化的Lorentz变换等等,视作局域的时空平移变换。无论怎样,引力的规范场论,始终与其他的规范场论有所不同,也许这是因为,前者与时空空间中的变换群有关而后者与内部空间上的变换群有关,或者说对引力而言,荷与惯性质量合二为一;而对其他规范场,荷是荷,惯性质量是惯性质量。
这就是我想同时请教你和sage兄的原因,如果你们两个同时从数学和物理的角度,给出同样的答案,那我心里有谱了
作者: 季候风 时间: 2010-12-23 22:01
再给一个理由:
广义相对论与规范理论的类比,在数学上相当于切丛与 “外在矢量丛” 的类比。
所谓 “外在向量丛”,就是在底流形坐标变换下,局部平凡化不变的丛。
(如果局部平凡化随着底流形坐标变换而变,则是 “张量丛” 或者 “旋量丛”。)
外在向量丛的规范变换是矩阵函数 (转移函数)
比如, SU(3) 规范理论的转移函数就是 3*3 矩阵值函数,满足幺正条件和行列式条件,
所以是 8 个独立函数决定的。
切丛则不同,其转移函数(即规范变换)是 Jacobi 矩阵
虽然含有 16 个函数,但它们来自于 4 个函数
所以在泛函意义上它们不是独立的,而只有原来的 4 个函数是 “独立” 的。
作者: 星空浩淼 时间: 2010-12-24 09:45 标题: 回复 13# 的帖子
季兄能否把最后一段说得更清楚一点?这个地方我没有听明白,谢谢!
有多少个独立函数,跟有多少个独立的导函数,是不同的——函数与函数的导函数,是相互独立的。一个自由度变量,跟它的对某参数的导数,是两个独立的自由度变量。
作者: 季候风 时间: 2010-12-24 22:39
几个参(函)数 “独立” 的意思,就我的理解,就是它们可以任意取。
最简单的比如四个平移参数,互相之间没有关系,“独立”,不存在约束,所以可以任取四个常数做坐标平移。
而一个函数的偏导数之间就存在约束。比如四元函数的四个偏导数之间就不是独立的。
任取四个函数,当然不一定正好构成一个四元函数的四个偏导数。
所以说,在切丛的转移矩阵(Jacobi 矩阵)中,矩阵元不能任取,存在约束。
但是广义坐标变换中四个函数
作者: faltings 时间: 2010-12-25 01:37 标题: 回复 15# 的帖子
不赞同,这儿的情况比frobenus定理包含的情况要大,不一定要可微。
矩阵就是对称的GL(4,R)
作者: sage 时间: 2010-12-25 03:20 标题: 回复 15# 的帖子
那我心里有谱了
=======================
For the peace of your mind, I completely agree with 季兄. I think he has explained it to you very well, I cannot do better. Let me just tell you some of my own ways of understanding it.
1) The standard statement is that general relativity is a gauge theory, gauging the space-time translation (Poincare).
To understand this statement, it is necessary to understand what do we mean by gauging a symmetry. Of course, we need to
start with a global symmetry of the system. At the same time, the very important consequence of gauging is the
introduction of new dynamics, new degrees of freedom (the gauge fields). We all know gauging U(1) E&M means that we must
introduce photon.
In this sense, it is easy to understand why Lorentz transformation is not being gauged. Starting with an inertia frame, Lorentz
boost will not introduce gravitational effect. However, to make equations covariant under Poincare, it is necessary to
introduce gravitational field.
2) Here is another way to count the number 4. Maxwell equation cannot fix all 4 components of the vector potential, because
the Maxwell equations are not independent. In fact, one relation (Bianchi) exist among them. Therefore, Maxwell equations will
leave one degree of freedom unfixed. We all know that this is the one gauge degree of freedom of U(1). Similarly, 10 Einstein
equations are not independent. Bianchi identities of the left-hand side means 4 degrees of freedom unfixed. And, we all know that
this is the 4 gauge degree of freedom of general relativity.
3) Here is my guess where the number 20 comes from. Einstein equations are in general 2nd order differential equations of g_munu.
In principle, the relevant physical quantities can be g_{munu} (10 d.o.f), first derivatives g_{munu,gamma} (40), secondary
derivatives g_{munu,alpha beta} (100). However, many of them can be transformed away by gauge transformations. Say I am doing a
general coordinate transformation, x->x'. The functions I can use (to transform g_munu is its derivatives) are (schematically,
and partial derivatives, of course) dx/dx' (16 of them), d^2 x/(dx'dx') (40 of them), d^3 x/(dx' dx' dx') (80 of them). Now the 10 of 16 dx/dx'
can be used to set g_{mu nu} to flat eta_munu. The rest of 6 belongs to Lorentz and rotation (which as we have discussed not relevant for
gravitational dynamics). Then we use the 40 d^2 x/dx'dx' to set all 1st derivatives g_{munu, gamma} to be zero. Then among the 100
2nd derivatives (g_{munu,alpha beta}), we can set 80 of them to zero by using 80 d^3x/(dx'dx'dx'). Therefore, there are 20 physical components
in Riemann tensor (can not be gauged away).
Most of what I said here is, of course, in Weinberg.
作者: 星空浩淼 时间: 2010-12-25 11:35
谢谢sage兄和季兄,这个问题,经过你们这么一讨论,我现在基本上有一点谱了
虽然还是存在一些疑问,只有随着我知识的增长,逐渐自己弄明白
[ 本帖最后由 星空浩淼 于 2010-12-26 11:37 编辑 ]
作者: Non 时间: 2010-12-25 14:37 标题: As for the extra 4 parameters
The extra 4 parameters are responsible for "changing" length in 4-dimension, having nothing to do with Poincare transformation (translation). You know Lorentz transformation conserves the "length" in 4-D.
[ 本帖最后由 Non 于 2010-12-25 06:40 编辑 ]
作者: 星空浩淼 时间: 2010-12-28 00:07 标题: 回复 19# 的帖子
我明白你说的意思了,谢谢!
其实只要拿支笔在纸上写一写就明白了:
x^μ=a^(μν)y_ν+a^μ
只要不再有“保持线元长度不变”这个限制,a^(μν)就有16个,再加上四个a^μ,共20个参数
在无穷小局域变换下,可以统一地看作是局域时空平移变换
[ 本帖最后由 星空浩淼 于 2010-12-28 09:39 编辑 ]
作者: 季候风 时间: 2010-12-28 03:10 标题: 回复 20# 的帖子
问题是这20个参数为常数的变换有任何物理意义吗?
作者: 星空浩淼 时间: 2010-12-28 09:50 标题: 回复 21# 的帖子
一般而言,时空中的变换群,若群参数为常数,则只是运动学意义上的变换群,对应运动学意义上的对称性。但是,这里仍然包含有只在广义相对论中才有的非平凡性——其中包含让四维时空线元长度任意改变的变换,这是在整体的彭家勒群变换中所没有的。
如果仅仅只是想知道到底有哪20参数,这可以提供一个答案,如此而已。有意义的,当然是局域化的变换群,此时就正如你所说,所有无穷小的局域变换,都对应局域的时空平移变换(不过跟整体时空平移变换群不同,此时群参数还是20个)。
[ 本帖最后由 星空浩淼 于 2010-12-28 20:26 编辑 ]
作者: 季候风 时间: 2010-12-29 01:19
呵呵,钻一下牛角尖:与其把这个作为 “20个参数”的解释,还不如放弃“20个参数”这种说法,
因为这种解释本身非常误导,暗示引力是把整个庞加莱对称性局域化的结果,而这并不正确。
作者: 星空浩淼 时间: 2010-12-29 08:40 标题: 回复 23# 的帖子
我见过不少专业文献,那里的确是把局域化的庞加莱对称性群看作是引力规范场论的部分规范对称群(比庞加莱更广泛的一般线性群,才是引力规范场论的全部规范对称性群),但我不知道自己记忆是否有误。
也许,这是一种历史上的一种约定成俗吧
[ 本帖最后由 星空浩淼 于 2010-12-29 09:41 编辑 ]
作者: sage 时间: 2010-12-29 12:14 标题: 回复 24# 的帖子
Do you have a reference?
If it is like you said, then the article you have seen is wrong. There is clear answer, not a matter of convention.
作者: 星空浩淼 时间: 2010-12-30 01:20 标题: 回复 25# 的帖子
我看的文献有点老(很可能过时了),比如80年代Mills有篇文章,综述规范场的基本思想。从此文中,Mills似乎表明,他给出non-Abel规范场,似乎是受启发于广义相对论对引力场的处理。今天的人却似乎颠倒了过来,用规范场的思想去解读广义相对论中的引力场。虽然一个涉及内部空间,一个涉及时空空间,从微分几何的角度来看,二者的确有着类似的数理逻辑,有着类似的思想框架。
Mills在这篇文章里,就提到即使是局域化的庞加莱群,也不能覆盖与引力相关的全部仿射变换群。同时他还说(大意):令人感到惊讶的是,能动张量是引力源,按照规范场论的逻辑框架,时空平移变换群应该就可以概括引力场的全部规范群,然后却发现事实并非如此。
在细节上,我不能保证有没有记忆错误。我看的是那篇文章的中文版,发表在国内80年代的《自然》杂志上
[ 本帖最后由 星空浩淼 于 2010-12-30 01:22 编辑 ]
整个真空弥漫这这种HIGGS场,而物质粒子的质量就是取决于它们与这个背景场的耦合大小。用个不是很准确的比方,这就像大鱼在水中游泳觉得惯性大,而小虾感觉惯性小,惯性大小就是质量。
源对场的作用
后文开始,保持和书上用的记号一致,用 代替
代替 。
。
如P20所述。源 会和场
会和场 耦合,使得场和无源时不同。其原因在于源与场的耦合会改变场的能量,(比如说真空中放入一个电子,就会改变电磁场的能量,)从而改变场的几率幅。作用量取极值的场也会相应地变化。
耦合,使得场和无源时不同。其原因在于源与场的耦合会改变场的能量,(比如说真空中放入一个电子,就会改变电磁场的能量,)从而改变场的几率幅。作用量取极值的场也会相应地变化。
这里有个观念上的变化。初次接触场,应该是中学里学到的电磁场。那时候,场被描述为源“产生”的东西,比如说电荷产生电场,电流产生磁场等。而按场论的观点,电荷和电场,一个是spin-1/2 Dirac场,一个是spin-1 电磁场,完全是两样东西。电荷并不会产生电场,而是因为和电场耦合,从而改变了电场——把电磁场从我们称之为“真空”的状态(这种状态我们以前认为是“没有场”的状态)变成另一种状态。
科普“上帝粒子” 精选
精选
后文开始,保持和书上用的记号一致,用
 代替
代替 。
。如P20所述。源
 会和场
会和场 耦合,使得场和无源时不同。其原因在于源与场的耦合会改变场的能量,(比如说真空中放入一个电子,就会改变电磁场的能量,)从而改变场的几率幅。作用量取极值的场也会相应地变化。
耦合,使得场和无源时不同。其原因在于源与场的耦合会改变场的能量,(比如说真空中放入一个电子,就会改变电磁场的能量,)从而改变场的几率幅。作用量取极值的场也会相应地变化。这里有个观念上的变化。初次接触场,应该是中学里学到的电磁场。那时候,场被描述为源“产生”的东西,比如说电荷产生电场,电流产生磁场等。而按场论的观点,电荷和电场,一个是spin-1/2 Dirac场,一个是spin-1 电磁场,完全是两样东西。电荷并不会产生电场,而是因为和电场耦合,从而改变了电场——把电磁场从我们称之为“真空”的状态(这种状态我们以前认为是“没有场”的状态)变成另一种状态。
科普“上帝粒子”
|||
原文发表于:http://zhenzhubay.com/upload/blog-2-1364.html 【版权所有,未经岳东晓许可,不得转载】
首先,“上帝粒子”这个词可能会引起很多人的反感,我第一次看到这个词就是如此。但习惯了这种通俗的叫法之后,比起叫它HIGGS波色子可能要更好懂一点。你也可以换个角度来看,牛顿就认为自己是上帝的使者,给人类带来宇宙的知识。牛顿之后的物理学家很少有人这么自我定位,但是物理学在杨振宁之后的迅猛发展真正使我们人类出走了蒙昧,在一套基本理论基础上,定量地理解了宇宙起源之后的几乎一切。
首先,“上帝粒子”这个词可能会引起很多人的反感,我第一次看到这个词就是如此。但习惯了这种通俗的叫法之后,比起叫它HIGGS波色子可能要更好懂一点。你也可以换个角度来看,牛顿就认为自己是上帝的使者,给人类带来宇宙的知识。牛顿之后的物理学家很少有人这么自我定位,但是物理学在杨振宁之后的迅猛发展真正使我们人类出走了蒙昧,在一套基本理论基础上,定量地理解了宇宙起源之后的几乎一切。
这个屡试不爽的基本物理理论有一个很普通的名字:“标准模型”(Standard Model),它的组成部分就是SU(2)xU(1)的弱点统一理论与SU(3)的量子色动力学。而这个”标准模型”是基于杨振宁发现的规范场理论,加上所谓对称自发破却的Higgs(希格斯)机制。过去的几十年中,围绕这个标准模型,物理学家进行了难以计数的计算,而这些计算又都与实验得到了几乎完美的吻合。每一次,大家都在发出感叹:标准模型还是对的。这对希望在理论与实验的差异中寻找新的突破的人们来说,是一次次的失望。对于另一群人来说,则可能是在变幻的世界中找到了不变的真理。
根据目前的数据,Higgs粒子很可能是找到了。在我继续科普之前,我们可以说,标准模型又对了。对于人类而言,这是值得庆贺的事情---我们的智力竟然可以窥破自然界如此深奥的秘密。这个秘密告诉我们也许最基本的问题,为什么我们有质量。或者说,我们的质量是从哪来的。
牛顿猜出了一个牛顿第二定律:F=ma,力等于质量乘以加速度。这是所有中学生都知道的。但牛顿无法告诉你质量从何而来。爱因斯坦写下 E =mc^2,但他也无法告诉你这个m从何而来。杨振宁创立了规范场理论,这个理论可以推导出所有的相互作用的方程,但是杨振宁的理论里物质粒子的质量只能是人为的加上。
把杨振宁的理论与Higgs的机制结合起来,就构成了我们前面提到的标准模型。所以,要科普“上帝粒子”,我们得先讲杨振宁。
物理学而且与其他自然科学不同,是一门精确科学,很多理论结果能有实验验证到小数点后10几位。但物理规律其实都是根据简单的不变性原理推导而来。比如说,今天的物理应该与昨天一样,从这个不变性,我们可以推导出能量守恒。一个实验在不同的位置进行,结果应该相同,由此我们得出动量守恒的原理。一个人在匀速运动的火车上应该得出与地上的人一样的物理规律,由此就导出了狭义相对论。爱因斯坦说,一个人在电梯里自由下落,感觉不到地球引力。由此原理,他导出了广义相对论---也就是引力理论。而由广义相对论,我们发现光线会引力作用下拐弯,恒星可能坍缩成黑洞,宇宙会爆炸、膨胀。
在杨振宁之前,人类真正能够写下方程的物理作用只有引力与电磁相互作用。这两种作用对于人类无疑是最直观的。引力无所不在。没有引力人连直立行走都很难,看看刘洋在天宫一号的努力就知道了。无论是闪电雷鸣,手机通讯,还是化学反应,包括生命运转的所有化学反应其实都是电磁作用的结果。引力与电磁作用的共同特点是他们的作用距离是无限远,因此人类能够进行宏观实验。通过实验,总结出它们的规律。牛顿发现,两个物体之间的引力与他们质量乘积成正比,与他们之间距离的平方成反比;类似的,电荷之间的作用力也与其电荷的乘积成正比,与距离的平方成反比。
随着物理学的发展,电磁相互作用成了一组严密而美妙的数学方程,这就是每一个科学与工程人士都应该熟知的麦克思维方程(Maxwell's equations)。它们是英法联军焚烧圆明园后的第二年英国物理学家 Maxwell根据前人的研究结果总结出来的电磁理论。直到今天,整个电机系的东东,基本上就是解这几个方程。而后,爱因斯坦以其天才的洞察力,发展了引力的几何理论---也就是广义相对论。
引力属于非常微弱的作用---试想,整整一个地球的引力才能把我们困在地面。而电磁作用也不强。当人类的探索走向微观,人们发现,物质原来蕴涵了巨大的能量。粒子之间强大的作用力,正是核能的源泉。在人类文明发端以来,宇宙起源之谜一直是一个哲学问题。而根据爱因斯坦的广义相对论方程以及相应的天文观测,人们已经知道,宇宙源于所谓大爆炸。如果反推到遥远的过去,整个宇宙都是充斥着巨高能量的粒子。而理解这一切,就需要像麦克斯韦尔方程那样的定量科学理论。
但是与引力与电磁力不同,粒子之间其他作用是非常短距离的。这个距离之短不是一跟头发的粗细,而是小于一根头发的万亿分之一,完全超出了可以直接观测的范围。人们迫切需要一种像爱因斯坦的广义相对论一样,没有任何实验数据却破空而出的惊世杰作,用纯粹理性把我们带进宇宙奥秘的神秘之门。在这个理论出现之前,世界上所有基本物理理论都不过是在盲人摸象而已。
1954年,也就是广岛原爆后9年,一位年轻的中国人发表了一篇现在称为YANG-MILLS规范场的论文。这篇标题看似平淡的论文在今天看来奠定了整个标准模型的理论基础。在这篇论文里,杨振宁博士以他绝不亚于爱因斯坦的洞察力,给出了所有相互作用的原理,以及对应的精确的数学方程。这就是我们今天经常听到的规范场理论。
与其他基本物理理论一样,规范场理论也是基于物理规律的不变性(搞物理的人也喜欢用对称性这个词),就是物理规律应该在某种变换下保持不变。如上所述,不变性原理推出了相对论以及动量量守恒等基本规律。当杨振宁把这种不变性扩展到基本粒子的量子理论,他惊人地发现,要使理论保持不变,就必须存在对应的相互作用。这就是所谓规范场。
具体来说,杨振宁发现,如果有两种粒子,那么它们之间的变化可以用一个2x2的复数矩阵描述,如果物理规律要在这种类型的局域变换下保持一致,则不能光有这两个粒子,还必须加一个相互作用。换言之,从本来没有考虑相互作用的自由粒子方程开始,一旦考虑规范不变原理,我们就必须要求粒子之间有相互作用,而且这个规范不变原理还告诉你相互作用应该是怎样的。读者如果没有理解这个原理的深刻以及其意义,应该认真思考一下。
杨振宁的2x2矩阵方程导致的理论称为 SU(2)规范场。我们今天已经知道,夸克之间的强相互作用是一种SU(3)的、精确的杨-米尔斯规范场(SU(3)也就是对应3x3的复数矩阵)。这个3,代表了一类夸克的三种颜色。强相互作用由夸克之间交换质量为0的所谓胶子(GLUON)完成。强相互作用(太阳内氢聚变成氦就是涉及强相互作用)的理论是杨振宁理论的简单与直接推广。
电磁力是由光子传递的,光子的零质量是电磁力距离无穷的原因。当时,人们认为,粒子之间的弱作用与强作用都是短程的,也就意味着其相互作用应该是由有质量的粒子传递(注)。但在杨振宁理论中,规范场粒子不能有质量---因为如果规范场有质量,物理方程就不能保持规范不变了。因此杨振宁论文刚刚问世的时候,其新颖的理论不为人所接受。特别是他遭到老一辈物理学家如Pauli等人的刁难式疑问。据传,在杨振宁之前,Pauli尝试了一种六维空间的爱因斯坦方程,但没有得到什么结果。而杨振宁的理论则无疑是一种现代的、深刻的革命性思维。
但科学发展的车轮是滚滚向前,不可阻挡的。无数物理学家前仆后继,开辟了人类从蒙昧走向文明的道路。规范场的质量产生问题的解决方案从似乎不相干的超导体理论得到了启发。
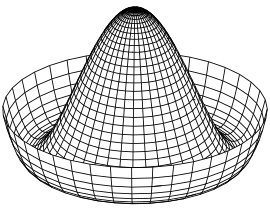
超导体大家都应该听说过的。如果你去医院做核磁共振检查,那台机器的核心部分就是一个超导体做的电磁铁。超导现象的第一个特征是没有电阻,一旦电流形成,可以永久的保持。但超导体还有一个更为基本的特征,那就是它完全排斥磁场----磁场不能从超导体中间通过。如果你去网上搜索,有很多这种超导演示的视频---一块超导体悬浮在半空之中(实际是在一块磁铁上空)。从理论物理的角度,这个现象意味着超导体内,光子获得了质量。对于这个质量的解释,苏联物理学家朗道提出了所谓朗道-金兹堡模型,在电子的电磁量子方程里凭空加了一项。这一项如果画一个图,像一个墨西哥帽子,中间突出,环绕着一圈低谷。与很多物理理论一样,这种模型的微观原理最初都没有解释,而是一种纯粹的灵感。但这个理论与实验得到了极好的吻合。基于基本原理的超导的微观理论的发现是在若干年之后,由所谓BCS理论完成。
有鉴于朗道-金兹堡模型成功地给零质量光子提供了质量(而且维持局域规范不变),固体物理学家安德森建议粒子物理学家们尝试类似的方案,也就是几乎空穴来风一般地在YANG-MILLS方程里加一个新的场。加入这个新的场之后,原本没有质量的规范场获得了质量,而规范场维持了其局域的规范不变。首先写出这个方程的人是Higgs。但他的论文寄出去被拒绝了,只好做了些修改之后再发给其他刊物。这是1964年的事情,也就是杨振宁论文发表后十年。
很多人在提到HIGGS机制的时候,喜欢使用对称自发破缺的说法,其实这是一个用词的谬误。实际上,HIGGS机制恰恰维持了YANG-MILLS规范场的局域不变性(local gauge invariance)。也就是说,规范不变才是王道。
数年之后,温伯格等人把 YANG-MILLS场与Higgs理论综合起来,用SU(2)xU(1)的规范场加上HIGGS场,成功构造了弱电统一理论。这个理论又很快得到了实验的验证,观测到了传播弱作用的三种规范波色子(W+/-、Z规范波色子)。
很多人在提到HIGGS机制的时候,喜欢使用对称自发破缺的说法,其实这是一个用词的谬误。实际上,HIGGS机制恰恰维持了YANG-MILLS规范场的局域不变性(local gauge invariance)。也就是说,规范不变才是王道。
数年之后,温伯格等人把 YANG-MILLS场与Higgs理论综合起来,用SU(2)xU(1)的规范场加上HIGGS场,成功构造了弱电统一理论。这个理论又很快得到了实验的验证,观测到了传播弱作用的三种规范波色子(W+/-、Z规范波色子)。
Higgs机制不仅给传播弱相互作用的规范场波色子(boson) 赋予了质量,还成了所有物质粒子(称为费米子,fermion, 如夸克与电子等)质量的来源。这是因为,与一般的场不同,Higgs场的真空值不为零。如下图所示,墨西哥帽子中心代表了HIGGS 场为0 的情况,而此处是一个尖顶,显然是不稳的,而稳定的状态是帽檐的沟谷处,这就代表HIGGS场的真空值不为0。整个真空弥漫这这种HIGGS场,而物质粒子的质量就是取决于它们与这个背景场的耦合大小。用个不是很准确的比方,这就像大鱼在水中游泳觉得惯性大,而小虾感觉惯性小,惯性大小就是质量。
Higgs粒子如果最终被证实,我们都应该庆祝。人类自古自问的一个问题,我们来自哪里,在标准模型-----也就是SU(2)xU(1)的弱电统一理论加上SU(3)的量子色动力学-----再一次得到实验证实之际,有了更为可靠的答案。2000年以前,人类还在迷信雷公电母、天狗吃日。今天,我们凭着自己的理性,掌握了自然界深层的机密。
但显然,标准模型不是终极真理,如同朗道模型一样,Higgs场背后必然有着更深刻的基本原理。
一旦我们进一步突破,或许我们的知识使我们能够构造一个全新的宇宙---也就是成为上帝。
----------------岳东晓 2012-07-05 于加州
注:我们现在知道,虽然gluon质量为零,但是由于规范场的非线性,导致所谓夸克囚禁
No comments:
Post a Comment