qiu: 黎曼提出的。他在他的教授就职演说《建构几何学的假设》中,利用尺度的无限小形式,引入了抽象空间,
"抽象空間
[PPT]請點選此處下載。
2005年11月15日 - 克萊茵(F. Klein)創造了一種解析的方法,通過賦與在單位圓盤上任意兩點的某種距離,給出雙曲幾何的一個模型。後人稱之為Klein模型。至此,人們 ...
2012年7月27日 - 高斯羅巴切夫斯基Bolyai Klein Model和非歐幾何的產生克萊茵(F. Klein)創造了
重庆市妇女联合会【精品-PPT】 - 道客巴巴
2013年8月13日 - 高斯Bolyai羅巴切夫斯基雙曲幾何1 3克萊茵( F. Klein) 創造了一種解析的方法, 通過賦與在單位圓盤上任意兩點的某種距離, 給出雙曲幾何的一個 ...
[PPT]請點選此處下載。
mathcenter.ck.tp.edu.tw/Resources/Ctrl/ePaper/ePaperOpenFileX.ashx?...
时空的历史_百度文库
wenku.baidu.com/view/59a43e0bba1aa8114431d97d.html?re=view
www.doc88.com/p-7989921694244.html
phymath999: "无穷小变换泛函" 泛函分析是研究拓扑线性空间 ...
phymath999.blogspot.com/2015/04/blog-post_60.html
轉為繁體網頁
轉為繁體網頁
可微映射的无穷小稳定性-数学辞海·第二卷 - 中国知网
mall.cnki.net/Reference/ref_readerItem.aspx?bid...recid...
轉為繁體網頁
轉為繁體網頁
曲率张量刻画了矢量二阶协变导数的不可交换性
"
为此目的,牛顿定义了一个时间的无限小瞬“o”,作为流数术的基础。这个无限小的时间瞬将引起流量的瞬,由此便能计算流数,即两个“瞬”的比值。比如说:如果有两个流量:x和y,它们都随时间变化,并且,它们之间有如下关系:
x3 + xy + y3 = 0
现在,无限小的时间瞬“o”便将引起两个流量的无限小的瞬,分别记为x’o, y’o。然后,在上述公式中分别用x+x’o, y+y’o代替x和y,再减去原式便得到:
3x2x’o+3x(x’o)2+(x’o)3+xy’o+x’oy+x’y’o2+3y2y’o+3y(y’o)2+(y’o)3 = 0
两边同时除以时间瞬“o”,然后再消去其中含有“o”的项,整理之后便能得到两个流数x’和y’之间的关系(两个变量的变化速率之比):
x’:y’ = -(3y2+x):( 3x2+ y)
牛顿用上例所述的方法,从位置变量的关系导出速度变量间的关系,与我们现在用微积分得到的结果一致。牛顿后来在他的《自然哲学的数学原理》一书中如此描述瞬时速度【4】:瞬时速度是指,当该物体移动到那一个非常时刻,既不是之前,也不是之后,流量间的最终比例。
"现代微分几何的源头:从高斯到黎曼
我的切身体会是,几何学家是好人。
——Jesse Dgoulas(1936yr. Fields)
历史的讲,黎曼几何是三维空间中曲线和曲面微分几何的自然演进。给定三维空间中的一张曲面S,我们有一个很自然地方式来给定其上切矢量的长度。只需把任意一点p处的向量内积<v,w>简单等同于三维空间中的标准内积,从而曲面上的(诱导)度量,长度概念也就有了。接下来,曲线长度的计算归结于速度矢量长度对参数的积分。事实上,有了度量概念,我们不但可以计算曲线长度,与此同时,曲线夹角、局部区域的面积计算等也都是水到渠成的事。总之,通常几何上的一切与测度概念都可以在曲面上展开。进一步,长度的概念还导致了一批特殊的曲线,即所谓的测地线,具有特殊的涵义:任给测地线上的两点p、q(严格的说,两点间不存在共轭点对儿),则p、q间的测地线距离小于等于任意连接这两点的曲线距离。想起初中平面几何课堂上一再重复的“两点间直线段最短”,我们有理由猜想测地线可以扮演“曲面上的直线”的角色。确实,测地线在一定意义上,被看作弯曲空间里的直线,这也是它们受到广泛重视的原因之一。
注意到,解析的讲,曲面上的度量概念,等价于在每一点定义一个正定的二次型(二次型系数都是曲线上的可微函数),亦称为曲面的第一标准形式。自高斯以来,第一标准形式的几何学几乎一直占据着微分几何的中心位置。
微分几何学发展史上极其浓墨重彩的一笔,或者说现代微分几何学的开山之作,是Gauss在1827年所发表的《关于曲面的一般研究》(一个英译版本可见Gauss,K.F., General Investigation of Curved Surfaces, Raven Press, New York, 1965)在这项工作中,Gauss在曲面上定义了一个所谓的曲率概念,来度量任意曲面在一点p附近,偏离切平面的程度。用现代的观点来看(事后诸葛亮地看)Gauss的核心想法是在曲面每一点处定义一个单位法向量,从而给出了从曲面到三维空间中单位球面的一个可微映射(如今这就称为高斯映射)。如果曲面S是可定向的,高斯映射是整体Well-Defined。在高斯时期,定向的概念还没有得到很好的关注。事实上,直到1865年,Mobius才在他提交的论文中给出了第一个不可定向的例子,即著名的Mobius带。现在定向是微分拓扑里的首要问题了,顺便提一下,按菲尔兹奖获得者Thom的观点,人们至今还没有完全挖掘出定向概念的真正内涵。
言归正传。高斯时期并没有整体的定向概念,所以他的“高斯映射”只是局部的定义在曲面片上(同样的原因,如今本科阶段的微分几何也只是讨论曲面片的微分几何)。不过,不管是整体的还是局部的,高斯建立了从任意曲面(片)到单位球面的高斯写像,这是一个可微映射,从而我们可以谈及其微分(众所周知,微积分的一半任务就是对可微映射取微分,直觉地讲,微分就是可微映射的局部一阶线性逼近,这是数学里惯用的把戏,因为线性映射是我们最得心应手的工具),从而诱导出从曲面切平面到单位球切平面的一个线性变换。Gauss把他的曲率定义成这个切映射的行列式,行列式越大弯曲程度越厉害,行列式为零正好对应着曲面上的平坦点域,这和我们的直觉是一样的。同样的论文里,Gauss还指出了,他的曲率正好与早些年间(1760年)Euler在曲面上任意点处所定义的两个主曲率的乘积相吻合,不同的是这个量后来被称为Gauss曲率,而不是Gauss-Euler曲率。
还是提一下Euler的主曲率概念吧(尽管其已黯然失神于高斯伟大贡献的光环之下)。早些年间,Euler用垂直于曲面的平面去截曲面,得到平面切痕曲线,自然可以定义其曲率,称方向曲率,旋转垂直平面的方向,得到一族方向曲率,所谓的欧拉主曲率,就是这一组曲率中最大的和最小的那两个。在欧拉时代,人们并不清楚一个关于主曲率的函数就可以完全地刻画曲面的弯曲程度,高斯的研究表明,两个主曲率的乘积就够了。
人们常说,曲率是现代黎曼几何的核心概念,这是指黎曼曲率张量。但要说明白曲率为何重要却不是件容易的事情,一个原因在于这不是仅凭直观的生活经验或直觉就能领略到的,必须借助一些严谨的数学演绎,总之必要的抽象是需要的,这也是至今“弯曲的时空”“时空扭曲”“内蕴弯曲”等概念一直让人费解的原因。很多科普书声称他用很生活化的语言,画几个图解释清了什么叫高维空间的曲率,其实他所写的东西往往与声称要解释的东西完全两码事。从分析的角度看,曲率张量刻画了矢量二阶协变导数的不可交换性,这确实与欧式空间的情况不同,因为我们明白通常的二阶偏导数可交换。而要从几何角度(真正地)理解曲率,要引入Jacobi场(广义相对论里叫测地偏离方程)概念,这应是另一篇博文的主题。
继续关注伟大的Gauss。高斯于1827年的文章中,有两个重要的创举:第一,高斯曲率仅仅依赖于曲面的度量,或者曲面的第一基本形式(称为高斯绝妙定理);第二,测地线所围成的三角形(测地三角形)内角和不一定等于180°,但它仅依赖于三角形区域的曲率积分。前者是内蕴几何学的开端,后者则与几何学上的“千年悬案”第五公设问题密切相关。
种种迹象表明,Gauss很清楚自己研究成果的深远意义。事实上,高斯时期的一个世纪难题是:判断欧几里得几何第五公设(初中几何第一课学过:过直线外一点有且只有一条直线与之平行)是否独立于另外几条公设。早些时候,第五公设等价于三角形内角和是180°,这是勒让德的工作(又一个生不逢时,不幸埋没于高斯光环下的伟大数学家。他与高斯的另一件“悲惨遭遇”是勒让德分布,被后人叫成高斯分布)。高斯的第二个发现表明,至少在二维情况下,可以构想一个几何体系,其性质完全依赖于其上的第一标准形式(而完全不依赖于外围空间)。在这种几何里,测地三角形(代替通常的平面三角形)的内角和依赖于曲率。事实上,Gauss确实验证了,它与180°的差量正好等于三角形区域上的曲率积分。这种几何体系不满足第五公设,但满足所有其它公设。然而,高斯当时并不具备足够的数学工具来发展他的几何构想(事实上,他缺少一个完备流形的概念,而这要等到二十世纪才由H.Weyl来给出)。另外,他也不愿意公开讨论这个备受争议的话题(我们知道高斯的谨小慎微是出了名的)。事实上,非欧几何学的诞生最后被正确的归功于俄国的Lobatchevski(1829)和Bolyai(1831),可想而知,这两位的理论都经历了相当长的争议期,后者甚至为此精神失常。注意到,他们的非欧几何学都不是从时髦的微积分入手的,如今它们只是数学博物馆里的精品。现代非欧几何的教材往往用微分几何的方式展开。
这里有必要说一下,提到Gauss,很难不让人产生一种天才情愫。各种描写高斯的史料里都渲染了一种个人英雄主义传奇色彩。一般来说,一个数学家一生中能产生三五个真正奇妙的想法就很满意了,而高斯一生中的灵感,可以说是雨后春笋般源源不断,真是让人没办法。读Gauss,伤不起啊伤不起…
回到正题。高斯的微分几何思想后来在1854年,被Riemann重新拾起(Riemann,B., On the hypotheses which lies at the foundation geometry一个英文版本可见Spivak的书)。尽管黎曼当年并没有一个恰当的微分流形概念,他不加证明的用直觉性的语言描述了我们今天所说的n维流形概念。循着高斯的心路历程,他在微分流形的每一点赋予一个正定二次型(如今称为Riemann度量),借助Gauss的内蕴曲率给出相应的Riemann截面曲率概念。进一步,黎曼陈述了一系列曲率与度量的关系。在接下来的几十年里,这些都被一一证明了。黎曼当年的就职演讲,使人相信,他的工作受当年几何学中的另一个问题的启发,即我们生存于其中的物理空间与几何学的关系。事实上,当时非欧几何学的诞生,已经使人们怀疑三维空间欧式几何的先验性。例如,当时Lobacheviski就曾设想宇宙空间应由他的双曲几何来描述,后因与天文观测不符而作罢。黎曼在当年的就职演讲里,已经提到这样的想法:物理空间到底应该由哪种几何来描述当由物理观测来判定;物质的存在可能使空间发生内蕴弯曲。注意到当时黎曼并没有四维时空(准确的说,叫Minkovski空间)的概念,因而,毫无疑问,广义相对论的创立要等到20世纪初期。当Einstein为他的引力理论缺少合适的数学而抓狂不已时,一位数学家好友(大学考试前时常借给他作业本)向他介绍了意大利学派Ricci,Levi Civita等他人正在研究的张量分析和黎曼几何。
就是Einstein也表示难以相信,半个世纪以前,即有人在数学上为广义相对论的萌芽奠定了基础。
毫无疑问,仅仅这篇就职演说,就可以让黎曼名垂青史,然而,在他短短的40年生命里,还有那么多令人惊叹的创见。值得一提的是,伟大如黎曼,其一生却未获得过任何奖项,仅有的几次报奖也因过于简短,证据不足而退回。真是冤哉枉也!
如今,当我们津津乐道以其名字命名的Riemann积分,Riemann假设,Riemann引理等概念时,是否想到过黎曼穷困潦倒,如流星般匆匆闪过历史苍穹的一生!也许,有这么多美妙的理论与之作伴,Riemann在天堂里的生活也不寂寞了。
谨以此篇,献给那些为追求真理,不慕容利默默奋斗的数学英雄们(00:26)
《数理同源》-2-谁发明了微积分 精选
精选

——Jesse Dgoulas(1936yr. Fields)
历史的讲,黎曼几何是三维空间中曲线和曲面微分几何的自然演进。给定三维空间中的一张曲面S,我们有一个很自然地方式来给定其上切矢量的长度。只需把任意一点p处的向量内积<v,w>简单等同于三维空间中的标准内积,从而曲面上的(诱导)度量,长度概念也就有了。接下来,曲线长度的计算归结于速度矢量长度对参数的积分。事实上,有了度量概念,我们不但可以计算曲线长度,与此同时,曲线夹角、局部区域的面积计算等也都是水到渠成的事。总之,通常几何上的一切与测度概念都可以在曲面上展开。进一步,长度的概念还导致了一批特殊的曲线,即所谓的测地线,具有特殊的涵义:任给测地线上的两点p、q(严格的说,两点间不存在共轭点对儿),则p、q间的测地线距离小于等于任意连接这两点的曲线距离。想起初中平面几何课堂上一再重复的“两点间直线段最短”,我们有理由猜想测地线可以扮演“曲面上的直线”的角色。确实,测地线在一定意义上,被看作弯曲空间里的直线,这也是它们受到广泛重视的原因之一。
注意到,解析的讲,曲面上的度量概念,等价于在每一点定义一个正定的二次型(二次型系数都是曲线上的可微函数),亦称为曲面的第一标准形式。自高斯以来,第一标准形式的几何学几乎一直占据着微分几何的中心位置。
微分几何学发展史上极其浓墨重彩的一笔,或者说现代微分几何学的开山之作,是Gauss在1827年所发表的《关于曲面的一般研究》(一个英译版本可见Gauss,K.F., General Investigation of Curved Surfaces, Raven Press, New York, 1965)在这项工作中,Gauss在曲面上定义了一个所谓的曲率概念,来度量任意曲面在一点p附近,偏离切平面的程度。用现代的观点来看(事后诸葛亮地看)Gauss的核心想法是在曲面每一点处定义一个单位法向量,从而给出了从曲面到三维空间中单位球面的一个可微映射(如今这就称为高斯映射)。如果曲面S是可定向的,高斯映射是整体Well-Defined。在高斯时期,定向的概念还没有得到很好的关注。事实上,直到1865年,Mobius才在他提交的论文中给出了第一个不可定向的例子,即著名的Mobius带。现在定向是微分拓扑里的首要问题了,顺便提一下,按菲尔兹奖获得者Thom的观点,人们至今还没有完全挖掘出定向概念的真正内涵。
言归正传。高斯时期并没有整体的定向概念,所以他的“高斯映射”只是局部的定义在曲面片上(同样的原因,如今本科阶段的微分几何也只是讨论曲面片的微分几何)。不过,不管是整体的还是局部的,高斯建立了从任意曲面(片)到单位球面的高斯写像,这是一个可微映射,从而我们可以谈及其微分(众所周知,微积分的一半任务就是对可微映射取微分,直觉地讲,微分就是可微映射的局部一阶线性逼近,这是数学里惯用的把戏,因为线性映射是我们最得心应手的工具),从而诱导出从曲面切平面到单位球切平面的一个线性变换。Gauss把他的曲率定义成这个切映射的行列式,行列式越大弯曲程度越厉害,行列式为零正好对应着曲面上的平坦点域,这和我们的直觉是一样的。同样的论文里,Gauss还指出了,他的曲率正好与早些年间(1760年)Euler在曲面上任意点处所定义的两个主曲率的乘积相吻合,不同的是这个量后来被称为Gauss曲率,而不是Gauss-Euler曲率。
还是提一下Euler的主曲率概念吧(尽管其已黯然失神于高斯伟大贡献的光环之下)。早些年间,Euler用垂直于曲面的平面去截曲面,得到平面切痕曲线,自然可以定义其曲率,称方向曲率,旋转垂直平面的方向,得到一族方向曲率,所谓的欧拉主曲率,就是这一组曲率中最大的和最小的那两个。在欧拉时代,人们并不清楚一个关于主曲率的函数就可以完全地刻画曲面的弯曲程度,高斯的研究表明,两个主曲率的乘积就够了。
人们常说,曲率是现代黎曼几何的核心概念,这是指黎曼曲率张量。但要说明白曲率为何重要却不是件容易的事情,一个原因在于这不是仅凭直观的生活经验或直觉就能领略到的,必须借助一些严谨的数学演绎,总之必要的抽象是需要的,这也是至今“弯曲的时空”“时空扭曲”“内蕴弯曲”等概念一直让人费解的原因。很多科普书声称他用很生活化的语言,画几个图解释清了什么叫高维空间的曲率,其实他所写的东西往往与声称要解释的东西完全两码事。从分析的角度看,曲率张量刻画了矢量二阶协变导数的不可交换性,这确实与欧式空间的情况不同,因为我们明白通常的二阶偏导数可交换。而要从几何角度(真正地)理解曲率,要引入Jacobi场(广义相对论里叫测地偏离方程)概念,这应是另一篇博文的主题。
继续关注伟大的Gauss。高斯于1827年的文章中,有两个重要的创举:第一,高斯曲率仅仅依赖于曲面的度量,或者曲面的第一基本形式(称为高斯绝妙定理);第二,测地线所围成的三角形(测地三角形)内角和不一定等于180°,但它仅依赖于三角形区域的曲率积分。前者是内蕴几何学的开端,后者则与几何学上的“千年悬案”第五公设问题密切相关。
种种迹象表明,Gauss很清楚自己研究成果的深远意义。事实上,高斯时期的一个世纪难题是:判断欧几里得几何第五公设(初中几何第一课学过:过直线外一点有且只有一条直线与之平行)是否独立于另外几条公设。早些时候,第五公设等价于三角形内角和是180°,这是勒让德的工作(又一个生不逢时,不幸埋没于高斯光环下的伟大数学家。他与高斯的另一件“悲惨遭遇”是勒让德分布,被后人叫成高斯分布)。高斯的第二个发现表明,至少在二维情况下,可以构想一个几何体系,其性质完全依赖于其上的第一标准形式(而完全不依赖于外围空间)。在这种几何里,测地三角形(代替通常的平面三角形)的内角和依赖于曲率。事实上,Gauss确实验证了,它与180°的差量正好等于三角形区域上的曲率积分。这种几何体系不满足第五公设,但满足所有其它公设。然而,高斯当时并不具备足够的数学工具来发展他的几何构想(事实上,他缺少一个完备流形的概念,而这要等到二十世纪才由H.Weyl来给出)。另外,他也不愿意公开讨论这个备受争议的话题(我们知道高斯的谨小慎微是出了名的)。事实上,非欧几何学的诞生最后被正确的归功于俄国的Lobatchevski(1829)和Bolyai(1831),可想而知,这两位的理论都经历了相当长的争议期,后者甚至为此精神失常。注意到,他们的非欧几何学都不是从时髦的微积分入手的,如今它们只是数学博物馆里的精品。现代非欧几何的教材往往用微分几何的方式展开。
这里有必要说一下,提到Gauss,很难不让人产生一种天才情愫。各种描写高斯的史料里都渲染了一种个人英雄主义传奇色彩。一般来说,一个数学家一生中能产生三五个真正奇妙的想法就很满意了,而高斯一生中的灵感,可以说是雨后春笋般源源不断,真是让人没办法。读Gauss,伤不起啊伤不起…
回到正题。高斯的微分几何思想后来在1854年,被Riemann重新拾起(Riemann,B., On the hypotheses which lies at the foundation geometry一个英文版本可见Spivak的书)。尽管黎曼当年并没有一个恰当的微分流形概念,他不加证明的用直觉性的语言描述了我们今天所说的n维流形概念。循着高斯的心路历程,他在微分流形的每一点赋予一个正定二次型(如今称为Riemann度量),借助Gauss的内蕴曲率给出相应的Riemann截面曲率概念。进一步,黎曼陈述了一系列曲率与度量的关系。在接下来的几十年里,这些都被一一证明了。黎曼当年的就职演讲,使人相信,他的工作受当年几何学中的另一个问题的启发,即我们生存于其中的物理空间与几何学的关系。事实上,当时非欧几何学的诞生,已经使人们怀疑三维空间欧式几何的先验性。例如,当时Lobacheviski就曾设想宇宙空间应由他的双曲几何来描述,后因与天文观测不符而作罢。黎曼在当年的就职演讲里,已经提到这样的想法:物理空间到底应该由哪种几何来描述当由物理观测来判定;物质的存在可能使空间发生内蕴弯曲。注意到当时黎曼并没有四维时空(准确的说,叫Minkovski空间)的概念,因而,毫无疑问,广义相对论的创立要等到20世纪初期。当Einstein为他的引力理论缺少合适的数学而抓狂不已时,一位数学家好友(大学考试前时常借给他作业本)向他介绍了意大利学派Ricci,Levi Civita等他人正在研究的张量分析和黎曼几何。
就是Einstein也表示难以相信,半个世纪以前,即有人在数学上为广义相对论的萌芽奠定了基础。
毫无疑问,仅仅这篇就职演说,就可以让黎曼名垂青史,然而,在他短短的40年生命里,还有那么多令人惊叹的创见。值得一提的是,伟大如黎曼,其一生却未获得过任何奖项,仅有的几次报奖也因过于简短,证据不足而退回。真是冤哉枉也!
如今,当我们津津乐道以其名字命名的Riemann积分,Riemann假设,Riemann引理等概念时,是否想到过黎曼穷困潦倒,如流星般匆匆闪过历史苍穹的一生!也许,有这么多美妙的理论与之作伴,Riemann在天堂里的生活也不寂寞了。
谨以此篇,献给那些为追求真理,不慕容利默默奋斗的数学英雄们(00:26)
《数理同源》-2-谁发明了微积分
|||
第一篇:微积分、变分等
注:微积分和经典力学关系密切,但它们是大家所熟知的基础学科。因此本篇在有关微积分的叙述中,主要以史话为主。“科学给人知识,历史使人智慧”,追溯科学发展史、了解大师们的思路历程,能启发我们的科学思维,预见科学的未来。从回顾变分法发展历史开始,将逐步增加一些更具体的数学物理内容。
1. 谁发明了微积分?【1,2】
妇孺皆知的大科学家中,除了爱因斯坦之外,牛顿当然得算一个,只不过年代稍微久远了一点。小学生应该都听过老师讲牛顿因苹果掉到头上而发现万有引力的故事。到了初中高中阶段选修物理课,便会学习到牛顿三大定律。大多数时候,牛顿是以一个伟大物理学家的形象存在于人们心目中的。其实,除了对物理学的贡献之外,牛顿还有不那么广为人知、发明了微积分的巨大功劳,这个作为伟大数学家的那一面,就往往被非数学或非理科专业的人们所忽略了。
不过,牛顿对物理和数学两个方面的贡献是互相联系起来的,可以说,牛顿最终是为了总结物体的力学运动规律而创造发明了微积分。没有适当的数学工具,物理定律不能成其为定律,只能算是经验之谈。
牛顿曾经有过一句经典名言:“如果说我比别人看的更远一点,那是因为我站在了巨人的肩膀上。”这句话也适用于他本人对微积分的贡献。话说回来,即使牛顿不发明微积分,自有其他的大师来完成这个工作,比如和牛顿同时共享微积分发明权的莱布尼兹就是一个。
牛顿和莱布尼兹的时代距离现在不过400年左右,而远在两千多年之前,古希腊的阿基米德所用的一些计算方法,已经靠近了积分思想的边缘。阿基米德发展了“穷竭法”,即类似于逐步近似求极限的方法,用以计算抛物线、弓形的面积以及椭球体、抛物面体等复杂几何体的表面积和体积。中国古代也有类似的记载,比如公元前4世纪,《庄子》的“一尺之棰,日取其半,万世不竭”;三国时期刘徽研究的割圆术等等,都忽闪着“无穷”、“极限”等现代数学思想的火花。也可以这么说,微积分的理论是牛顿和莱布尼兹等建立的,但计算方法,特别是类似积分的方法,却早已有之。
什么是微积分?为什么两千多年前的科学家就已经会计算复杂形状的面积和体积,却直到几百年前的牛顿时代才真正创建了微积分?这其中的本质原因可以说是与物理及天文方面的发展密切相关。微积分创立之前的数学工具,研究对象和解决的问题都是属于静态的。即使积分的方法,如果不是将它看成微分的逆运算的话,也是一种静态的思想。精确而瞬时的动态计算必然要涉及到微分的概念。所以,将微分和积分的理论统一起来的微积分学,本质上是一种运动的数学,或称变量的数学。到了16-17世纪,以变量为基础的运动学和动力学的发展向数学提出了挑战,最终才促进了微积分理论的建立,而微积分反过来又加速了牛顿力学的发展,这是数学物理同源的第一次历史渊源。
在17世纪初期,伽利略(1564-1642)和开普勒(1571-1630)在天体运动中所得到的一系列观察结果和实验事实,导致科学家们对新一代数学工具的强烈需求,也激发了新型数学思想的诞生。从大量的数据中,如何才能抽象出大自然的秘密—物体的运动规律来呢?
这些数据中的大多数,有一个共同特点,就是表现了某物体在空间的位置,随着观测的时间而变化。
比如,在伽利略的时代,已经有了速度的概念。那时的科学家们已经知道:速度是物体运动快慢的标志。某物体经过一定的时间,在空间走了一定的距离,这段距离被这段时间相除,不就得到了速度嘛。如果物体运动的快慢始终一样,那就叫匀速运动,否则就是非匀速运动。伽利略从实验结果中发现,在地球引力持久作用下物体的运动,快慢并非始终一致的,开始时下落得比较慢,后来则下落得越来越快,也就是说,每经过一段时间的下落,速度就有所增加。伽利略又发现,无论是在下落的开始还是最后,速度这种增加的效果(或是,速度增加的速度)是一样的,这也就是我们现在所熟知的说法:“地面上自由落体的运动是一种等加速度运动”。
速度、加速度、匀速、匀加速、平均速度、瞬时速度,……,现在的学生很容易理解这些概念,那得感谢我们有了好用的数学工具:极限的概念和微积分的方法。但在当时,这些名词却曾经困惑过像伽利略这样的大师们。从定义平均速度,到定义瞬时速度,是概念上的一个飞跃。平均速度很容易计算:用时间去除距离就可以了。但是,如果速度和加速度每时每刻都在变化的话,又怎么办呢?那时候,平均速度应该被定义在更短的时间间隔中。当时间间隔变小,运动的距离也变小,距离除以时间,仍然能得到一个速度!但问题是:当时间间隔变到0,就没法作除法了啊!不过又一想:时间为0时,距离也为0!这样,人类第一次碰到了0除0的难题。
可以相信,开普勒在总结他的行星运动三定律时,也曾经有类似的困惑。开普勒得出了行星运动的轨迹是个椭圆,他也认识到行星沿着这个椭圆轨迹运动时,速度和加速度的方向和大小都在不停地变化。但是,他尚未有极限的概念,也没有曲线的切线及法线的相关知识,不知如何描述这种变化,于是,便只好用“行星与太阳的连线扫过的面积”这种静态积分量来表达他的第二定律。
牛顿1643年出生时,伽利略和开普勒均已去世。两位大师将他们的成果和困惑都留在了世界上,等待后人的传承。除了这两位学者之外,法国数学家笛卡尔(1596-1650)对牛顿的数学思想影响很大。笛卡尔在几何中引入坐标系,将几何和代数、形与数、统一起来。此外,笛卡尔在曲线的研究中已经引入了变量的思想,将几何学中求切线、曲率之类的问题与变量概念相联系,才使得后来有了“微积分”这个划时代的革命。
科学史上的诸多发现,都既有它们历史的必然(那是“巨人的肩膀”),又颇具偶然趣味的一面(比如“苹果打头上”)。微积分的创立也是如此。
1665年5月,可怕的瘟疫蔓延伦敦,剑桥大学被迫关门。刚完成学士学位,准备以教授助手的身份继续攻读深造的牛顿回到乡下的老家住了18个月。这短短的一年多被后人称为牛顿的“奇迹年”。从他这段时期写下的《杂录》可以看出,这一年时间里牛顿在科学上成果累累:创立了流数术(微积分),并建立了万有引力定律和光学分析的基本思想。由此可见,做科研的人,一段时期的修整和度假,静下心来思考,是很有必要的。试想如果没有这一年多的瘟疫,牛顿成天忙碌于工作和学习之中的话,是否还能有如此大的创造性的成就呢?起码,微积分创立的时间恐怕会推迟一点。
从剑桥回家乡之前,牛顿正在思考二项式展开的问题,并由此对“无穷”的概念有所突破。在这一点上,22岁的牛顿初出茅庐,就在数学思想上超越了前辈笛卡尔。笛卡尔的一些想法如今听起来颇为有趣:他认为人的大脑不是无穷的,所以不应该去思考与无穷有关的问题。但牛顿没有被这位名人的说法吓倒,有限的脑海中怎么也放不下这个无穷级数的问题!比如,他有次在他的《杂录》笔记本上,画了一条双曲线,写下了如下的公式来计算曲线下的面积:
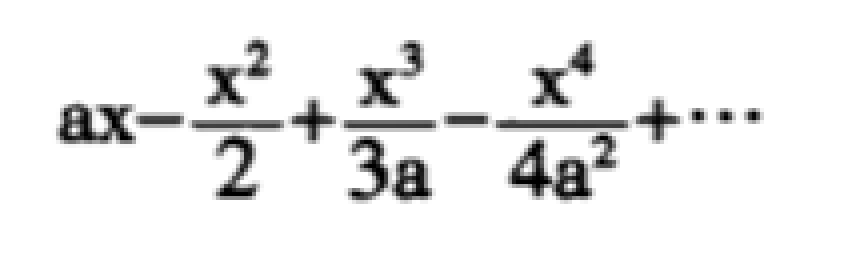
得到上述的公式要用到二项式的分数幂展开。牛顿当时已经把它看成是一个无穷多项之和,但他认为,一个无穷序列并不等于要做无穷多的计算,可见22岁的牛顿已经有了“极限”和“收敛”的概念。并且事实上,牛顿对此序列进行了大量的计算,一直算到了小数点后55位,写下2000多个数字,整整齐齐地排列在他的笔记本上。从这个例子也可以看出,牛顿的新数学思想并非凭空产生,而是建立在大量艰苦运算的基础之上。
无穷多项求和的概念,又引导牛顿进一步思考无限细分下去而得到的无穷小量问题。他将这无穷小量称之为“极微量”,即现代所熟知的微分。再进一步,牛顿将几何学中求切线、曲率之类的问题与物理中运动学的问题合二为一。在笔记中,牛顿将求解此类无穷小问题的种种方法称为流数法(Methodof Fluxions),包括正流数术(微分)和反流数术(积分)。1665年5月20日,牛顿第一次在他的手稿上描述他的“流数术”,实质上就是现代微积分的思想。因此,后人便把这一天作为微积分的诞生日。
在“流数术”中【3】,牛顿将运动学中如位置一类的变量称为“流量”(用x、y、z表示),而将流量的变化率,即速度,称之为“流数”。流数用x、y、z上面加一点来表示(此文中用x’,y’,z’表示),这类符号一直沿用至今。
牛顿认为他的流数术的目的就是要解决如下的问题:
1. 知道流量之间的关系,如何求流数之间的关系?(微分),
2. 以及问题1的逆问题(相当于积分)。
为此目的,牛顿定义了一个时间的无限小瞬“o”,作为流数术的基础。这个无限小的时间瞬将引起流量的瞬,由此便能计算流数,即两个“瞬”的比值。比如说:如果有两个流量:x和y,它们都随时间变化,并且,它们之间有如下关系:
x3 + xy + y3 = 0
现在,无限小的时间瞬“o”便将引起两个流量的无限小的瞬,分别记为x’o, y’o。然后,在上述公式中分别用x+x’o, y+y’o代替x和y,再减去原式便得到:
3x2x’o+3x(x’o)2+(x’o)3+xy’o+x’oy+x’y’o2+3y2y’o+3y(y’o)2+(y’o)3 = 0
两边同时除以时间瞬“o”,然后再消去其中含有“o”的项,整理之后便能得到两个流数x’和y’之间的关系(两个变量的变化速率之比):
x’:y’ = -(3y2+x):( 3x2+ y)
牛顿用上例所述的方法,从位置变量的关系导出速度变量间的关系,与我们现在用微积分得到的结果一致。牛顿后来在他的《自然哲学的数学原理》一书中如此描述瞬时速度【4】:瞬时速度是指,当该物体移动到那一个非常时刻,既不是之前,也不是之后,流量间的最终比例。
那时的牛顿只不过是一个二十出头的小伙子,一定还没有意识到自己这个发现对科学的重大意义,即使到了后来的1669年至1676年间,牛顿就“流数术”写下了三篇重要论文时,也并没有将文章及时地在期刊上公开发表,而只是让它们在朋友中和一些英国科学家中传阅。
德国数学家萊布尼茨(1646-1716)在对几何的研究中,独立于牛顿也走向了创建微积分的道路。他分别于1684年和1686年发表了微分和积分的论文。如果也追溯笔记本上的记录的话,萊布尼茨是在1675年底建立了微积分学,比起牛顿最早的笔记记录晚了10年左右,但萊布尼茨却早于牛顿3年在期刊上发表了他的结果。也许牛顿后来大彻大悟,意识到了这个“微积分”发明权的重要性,在1711年左右与萊布尼茨掀起了一场激烈的发明权之争。这时候牛顿已经是英国皇家学会的会长,在科学界大名鼎鼎,却仍然难以克服人性的弱点。虽然牛顿在公开场合假装与此事件无关,但是仍然掩盖不了暗地里争名夺利的小肚鸡肠,他不符合程序地亲自起草了该事件的调查报告,还匿名写文章攻击莱布尼茨窃取他的成果。这次争论大大地干扰了两位学者的正常生活。

不过后来,经过历史考证,萊布尼茨和牛顿的方法和途径均不一样,对微积分学的贡献也各有所长。牛顿注重于与运动学的结合,发展完善了“变量”的概念,为微积分在各门学科的应用开辟道路。萊布尼茨从几何出发,发明了一套简明方便使用至今的微积分符号体系。因此,如今学术界将微积分的发明权判定为他们两人共同享有。
微积分学刚建立时,因为它对极限概念缺乏严密的定义而受到攻击。例如推导瞬时速度时所用的无限小时间瞬“o”到底是个什么东西?到底是不是0呢?攻击者们认为牛顿自己的说法也是含混不清的,在用它作除法的时候,说它不是0而可以作除法,做完除法之后,又说它是0而将后面的项都甩掉!这不就是一种诡辩术么?这些质疑当时被称为“无穷小悖论”。但是无论如何,大多数人发现微积分学即使不严密但仍然好用,用它解决了各门学科中的许多疑难问题。直到后来19世纪,在柯西、达朗贝尔、外尔斯特拉斯等数学家们的努力下,才将微积分的概念在数学逻辑上严格化、完整化,并由此迈向了更深奥的解析学及微分方程理论。因此,微积分的创建是数学史上,也是科学史上的一件大事,为各门学科的发展立下了不朽功勋。
参考资料:
No comments:
Post a Comment