[PDF]全像原理: 場論與重力的世紀婚禮
January 24, 2015
高斯绝妙定理指出,这片披萨必须有至少一个方向永远保持平整——不管你怎么弯,它一定会留下一点“平”的痕迹。
http://www.guokr.com/article/439344/
高斯绝妙定理指出,这片披萨必须有至少一个方向永远保持平整——不管你怎么弯,它一定会留下一点“平”的痕迹。
相反,鸡蛋壳两个方向上都是弯的。这是它的关键。用数学语言表达,那就是这些双重弯曲的曲面拥有非零的高斯曲率。像我们先前遇到的橘子皮一样,这意味着它们不可能被压平,除非有撕裂或者拉伸——有高斯绝妙定理保证这一点。要打破一个鸡蛋,你必须首先弄出一个坑。等到鸡蛋失去了弯曲,也就失去了强度
数学

(Ent/编译)我们都遇到过这种情况。你抓起一块披萨,正要一口吞掉的时候,披萨一下子软了,从你的指尖处耷拉了下来。披萨饼本身的结构强度不够高,无法支持整片的重量。也许下次应该少加点儿料?不用,无需绝望。
如果是是个吃披萨多年的老手,那你应该知道怎么对付这样的场景:只需把披萨弯成U形即可。(手头没有披萨?拿一张纸试验一下就好。)
 一张纸拿在手里就会耷下去,但弯曲握就能让它笔直。为什么呢?图片来源:Aatish Bhatia
这个披萨小窍门的背后,深藏着一项关于曲面的强力数学。这一数学发现如此绝妙,以至于它的发明人——数学天才卡尔·弗雷德里克·高斯(Carl Friedrich Gauss)——给它起了个拉丁文名叫Theorema Egregium,意思是“绝妙定理”。
一张纸拿在手里就会耷下去,但弯曲握就能让它笔直。为什么呢?图片来源:Aatish Bhatia
这个披萨小窍门的背后,深藏着一项关于曲面的强力数学。这一数学发现如此绝妙,以至于它的发明人——数学天才卡尔·弗雷德里克·高斯(Carl Friedrich Gauss)——给它起了个拉丁文名叫Theorema Egregium,意思是“绝妙定理”。
拿一张纸,卷成圆柱形纸筒。你可能觉得显而易见,纸本来是平的,卷成筒就弯了,对吧?可是高斯不这么想。他想给纸的弯曲程度(“曲率”)下一个定义,让它不因你人工施加的弯曲而改变。
 图片来源:Aatish Bhatia
如果你放大去看一只生活在纸筒上的蚂蚁,这只蚂蚁可以走很多条不同的路线。它可以沿着弯曲道路横着走下去,画出一个圆;也可以沿着平坦路线竖着走,走出一条直线。或者它可以把两种方式组合起来,走一条螺旋。
图片来源:Aatish Bhatia
如果你放大去看一只生活在纸筒上的蚂蚁,这只蚂蚁可以走很多条不同的路线。它可以沿着弯曲道路横着走下去,画出一个圆;也可以沿着平坦路线竖着走,走出一条直线。或者它可以把两种方式组合起来,走一条螺旋。
高斯的天才在于,他想到把所有这些路线都纳入曲率定义里面。办法是这样的:从任何一点出发,找到这只蚂蚁能选择的最极端的两条路线——也就是最凹的和最凸的两条线。然后把它们的曲率乘起来。凸的路线曲率是正的,凹的路线曲率是负的,直的路线曲率是0。你得到的数字,就是那个点上的高斯曲率。
 图片来源:Aatish Bhatia
举几个例子吧。对于纸筒上的蚂蚁来说,最极端的两条路,一条是横着画圆,另一条就是竖着画直线。但是因为直线具有0曲率,所以乘起来总是得到0。照数学家的说法,纸筒是平的——它的高斯曲率就是0。这正是因为你能用平整的纸张卷出一个纸筒。
图片来源:Aatish Bhatia
举几个例子吧。对于纸筒上的蚂蚁来说,最极端的两条路,一条是横着画圆,另一条就是竖着画直线。但是因为直线具有0曲率,所以乘起来总是得到0。照数学家的说法,纸筒是平的——它的高斯曲率就是0。这正是因为你能用平整的纸张卷出一个纸筒。
相反,如果蚂蚁活在一个球上,那么它就无法找到平坦的路线,每一条道路都会有一定程度的向外凸出,所以高斯曲率一定是个正的数。所以,球是弯的,而筒是平的。你可以把一张纸卷成一个筒,却永远不能卷成一个球。
 图片来源:Aatish Bhatia
高斯的绝妙定理就是:生活在曲面上的蚂蚁,根本不需要离开它就能知道曲面的曲率。只要测量一下距离,计算一下就行。顺便说,这也是为什么我们没有离开宇宙却能测量出我们的宇宙是不是平的(根据目前的观测来看,它是)。
图片来源:Aatish Bhatia
高斯的绝妙定理就是:生活在曲面上的蚂蚁,根本不需要离开它就能知道曲面的曲率。只要测量一下距离,计算一下就行。顺便说,这也是为什么我们没有离开宇宙却能测量出我们的宇宙是不是平的(根据目前的观测来看,它是)。
但这个定理还有一个绝妙的结果:你可以随意弯曲一个曲面,只要你不拉长、压缩或者撕裂它,高斯曲率一定不会变。因为单纯弯曲不改变其上的距离,所以不管怎么弯,上面的蚂蚁总会计算出同样的高斯曲率。
听起来可能有点儿抽象,但是这推论有十分紧贴现实的结果。把一个橘子切成两半,吃掉里面的东西,然后把剩下半个橘子皮放在地上,踩吧。皮永远不可能被踩扁成一个完整的圆。相反,它一定会裂开。这是因为球面和平面拥有不同的高斯曲率,所以不扭曲、不撕裂,是不可能把球面压平的。有没有试过给人寄篮球当礼物?包装纸会遇到完全一样的问题。不管你怎么弯曲一张纸,它总会留下一点点“平”的痕迹,所以最后只能得到皱皱巴巴一团糟。
 桔子皮不可能压成完整圆——因为球面和平面高斯曲率不同(而且桔子皮也没有什么延展性)。图片来源:Aatish Bhatia
这个定理的另一个推论是,平面纸上永远不可能画出准确的地图。很多常见世界地图投影方式能精确地保留角度,但是在面积上就有严重误差。数学博物馆的推特指出,服装设计师也面临类似挑战——他们在平面上设计花样,却要符合弯曲的人体。
桔子皮不可能压成完整圆——因为球面和平面高斯曲率不同(而且桔子皮也没有什么延展性)。图片来源:Aatish Bhatia
这个定理的另一个推论是,平面纸上永远不可能画出准确的地图。很多常见世界地图投影方式能精确地保留角度,但是在面积上就有严重误差。数学博物馆的推特指出,服装设计师也面临类似挑战——他们在平面上设计花样,却要符合弯曲的人体。
 每个红色圆圈的实际面积是相等的,但在地图上看起来就有很大的差异。图片来源:Stefan Kühn (左), Eric Gaba (右) / Wikimedia
那这一切和披萨饼有什么关系呀?是这样的:你拿起披萨之前,它是平的(数学上说,它的高斯曲率为0)。高斯绝妙定理指出,这片披萨必须有至少一个方向永远保持平整——不管你怎么弯,它一定会留下一点“平”的痕迹。当这片披萨塌下去的时候,平的方向(红色箭头)是朝侧面的,这对吃掉它可没有什么帮助。但是如果你抢在它塌下去之前,先把披萨侧着捏弯,就迫使另一个方向只能保持平整——也就是对着你嘴巴的方向。还真是绝妙的定理呀。
每个红色圆圈的实际面积是相等的,但在地图上看起来就有很大的差异。图片来源:Stefan Kühn (左), Eric Gaba (右) / Wikimedia
那这一切和披萨饼有什么关系呀?是这样的:你拿起披萨之前,它是平的(数学上说,它的高斯曲率为0)。高斯绝妙定理指出,这片披萨必须有至少一个方向永远保持平整——不管你怎么弯,它一定会留下一点“平”的痕迹。当这片披萨塌下去的时候,平的方向(红色箭头)是朝侧面的,这对吃掉它可没有什么帮助。但是如果你抢在它塌下去之前,先把披萨侧着捏弯,就迫使另一个方向只能保持平整——也就是对着你嘴巴的方向。还真是绝妙的定理呀。
 没想到几何学也能这么美味吧。图片来源:Aatish Bhatia
在一个方向上弯曲,来迫使它在另一个方向上保持平直。一旦你理解了这个点子,你就会到处都看到它。仔细看看一片草叶。它通常都是沿着中央叶脉弯曲的,这能帮助它维持笔直,不会软塌下去。工程师经常用弯曲来强化结构承载力。在马德里扎祖拉体育场,西班牙结构工程师埃杜拉多·托罗亚(Eduardo Torroja)设计了一套创新的混凝土屋顶,从边缘一直伸到看台上方,遮蔽了大片区域,而厚度只有几厘米。这其实就是披萨技巧。
没想到几何学也能这么美味吧。图片来源:Aatish Bhatia
在一个方向上弯曲,来迫使它在另一个方向上保持平直。一旦你理解了这个点子,你就会到处都看到它。仔细看看一片草叶。它通常都是沿着中央叶脉弯曲的,这能帮助它维持笔直,不会软塌下去。工程师经常用弯曲来强化结构承载力。在马德里扎祖拉体育场,西班牙结构工程师埃杜拉多·托罗亚(Eduardo Torroja)设计了一套创新的混凝土屋顶,从边缘一直伸到看台上方,遮蔽了大片区域,而厚度只有几厘米。这其实就是披萨技巧。
 弯曲的草叶。图片来源:Dudley Carr / Flickr
弯曲的草叶。图片来源:Dudley Carr / Flickr
 西班牙扎祖拉体育场。图片来源:Ximo Michavila
弯曲带来力量。想想看:你能站在一个空易拉罐上,它能轻松承载你的体重;可是易拉罐外壁的厚度差不多和纸一样薄。它的秘密就是它的弯曲。如果有人趁你站在上面的时候拿笔戳一下易拉罐,就能戏剧化地展现这一点——只需一个小凹坑,它就会在你脚下轰然崩塌。
西班牙扎祖拉体育场。图片来源:Ximo Michavila
弯曲带来力量。想想看:你能站在一个空易拉罐上,它能轻松承载你的体重;可是易拉罐外壁的厚度差不多和纸一样薄。它的秘密就是它的弯曲。如果有人趁你站在上面的时候拿笔戳一下易拉罐,就能戏剧化地展现这一点——只需一个小凹坑,它就会在你脚下轰然崩塌。
 纸板箱里隐藏的秘密。图片来源:Craig Sunter / Flickr
但最日常的例子可能是无处不在的波形建材。世界上简直没有比纸板箱更无聊的东西,但是撕开一个这样的箱子,你会看到箱壁里一条熟悉的波浪曲线。这些皱褶在里面可不是为了好看,它们是一种天才的结构方式:让材料又薄又轻,又能坚硬到足以承担可观的重压。
纸板箱里隐藏的秘密。图片来源:Craig Sunter / Flickr
但最日常的例子可能是无处不在的波形建材。世界上简直没有比纸板箱更无聊的东西,但是撕开一个这样的箱子,你会看到箱壁里一条熟悉的波浪曲线。这些皱褶在里面可不是为了好看,它们是一种天才的结构方式:让材料又薄又轻,又能坚硬到足以承担可观的重压。
 很多人小时候玩过的把戏:把一张纸折叠几次就能承载很大的重量,但它背后的数学可能你就想不到了。图片来源:Aatish Bhatia
波形金属板使用的也是同样的原理。这些不起眼的建材是纯实用性的体现,它们的形态和其功能完美契合;它们的高强度和相对低廉造价使其成为了整个现代世界的背景。
很多人小时候玩过的把戏:把一张纸折叠几次就能承载很大的重量,但它背后的数学可能你就想不到了。图片来源:Aatish Bhatia
波形金属板使用的也是同样的原理。这些不起眼的建材是纯实用性的体现,它们的形态和其功能完美契合;它们的高强度和相对低廉造价使其成为了整个现代世界的背景。
今天,我们就算看到这些波浪形金属板也几乎不会多想什么。但当它们诞生时,许多人把波形建材看成是奇迹材料。1829年,亨利·帕尔默(Henry Palmer)获得了波形建材的专利,他是一个英国工程师,负责建造伦敦码头。帕尔默建起了世界上第一个波形钢结构建筑——伦敦码头的松油棚屋。虽然它今天看来可能没什么了不起,但是听听当时的一家建筑学杂志是怎么描述它的吧:
虽然波形建材和易拉罐的强度可以很高,但有个办法让这些材料变得更强。想自己找到这个办法?去冰箱拿个鸡蛋出来。放在掌心,整只手握住鸡蛋,挤吧。(尝试这个的时候记得别戴戒指。)你会为它的强度而惊讶的。我就没法把鸡蛋握坏,哪怕用尽全力也没戏。(真的,谁试谁知道。)
 请务必在家中尝试一下——好吧,为了安全,别在电脑前尝试。图片来源:Aatish Bhatia
鸡蛋为什么这么强?易拉罐和波形金属板在一个方向上是弯的,另一个还是平的。这一弯曲让它们拥有了一定强度,但它们还是有可能被压成本来的平板。
请务必在家中尝试一下——好吧,为了安全,别在电脑前尝试。图片来源:Aatish Bhatia
鸡蛋为什么这么强?易拉罐和波形金属板在一个方向上是弯的,另一个还是平的。这一弯曲让它们拥有了一定强度,但它们还是有可能被压成本来的平板。
相反,鸡蛋壳两个方向上都是弯的。这是它的关键。用数学语言表达,那就是这些双重弯曲的曲面拥有非零的高斯曲率。像我们先前遇到的橘子皮一样,这意味着它们不可能被压平,除非有撕裂或者拉伸——有高斯绝妙定理保证这一点。要打破一个鸡蛋,你必须首先弄出一个坑。等到鸡蛋失去了弯曲,也就失去了强度。
 图片来源:Owen Cliffe / Wikimedia
核电站冷却塔的象征性形状也在两个方向上利用了弯曲。这个形状叫做双曲面,能让所需的材料最少。正常的烟囱很像巨大易拉罐——结实是结实,但是很容易弯。双曲面形状的烟囱靠双向弯曲来解决这个问题,这样的弯曲方式能把形状“锁死”在空间中,提供额外的强度。
图片来源:Owen Cliffe / Wikimedia
核电站冷却塔的象征性形状也在两个方向上利用了弯曲。这个形状叫做双曲面,能让所需的材料最少。正常的烟囱很像巨大易拉罐——结实是结实,但是很容易弯。双曲面形状的烟囱靠双向弯曲来解决这个问题,这样的弯曲方式能把形状“锁死”在空间中,提供额外的强度。
另一种得益于弯曲的形状是品客“薯片”,照数学家的说法,这是个双曲抛物面(hyperbolic paraboloid,舌头打结了没?)。
 图片来源:Aatish Bhatia
自然界运用这一形状的招数堪称脑洞大开。濑尿虾有一项臭名昭著的本领——动物界里最快的拳击手,它的一拳打出去的力道足以把着力点上的水蒸发掉,创造出冲击波和闪光。要想使出这死亡一击,濑尿虾使用了双曲抛物面形状的“弹簧”。平时它把弹簧压缩起来储存巨大的能量,然后一招之内释放出来。
图片来源:Aatish Bhatia
自然界运用这一形状的招数堪称脑洞大开。濑尿虾有一项臭名昭著的本领——动物界里最快的拳击手,它的一拳打出去的力道足以把着力点上的水蒸发掉,创造出冲击波和闪光。要想使出这死亡一击,濑尿虾使用了双曲抛物面形状的“弹簧”。平时它把弹簧压缩起来储存巨大的能量,然后一招之内释放出来。
西班牙-墨西哥建筑师菲利克斯·坎德拉(Félix Candela)很懂薯片形状的力量。坎德拉是托罗亚的学生,他的建筑将双曲抛物面带到了新的高度(字面意思)。当你听到“混凝土”这个词的时候,恐怕只会想到无聊透顶的方块建筑,但坎德拉却利用双曲抛物面盖起了巨大的建筑,使用的混凝土薄到不可思议。身为这一材料的真正大师,他既是极富创新的建筑者,也是结构艺术家。
 图片来源:Ciudad de las Artes y las Ciencias / Flickr
所以为什么薯片形状强度如此之高?这和它平衡张力与压力的方式有关。一切建筑都要支撑重量,最终将这些重量传递到地面上。这一传递可以靠两种不同方式完成:其一是压缩,拱顶就是纯靠压力而实现的例子;另一个就是拉伸,把一根锁链拎起来,它的每一环就都处于拉伸状态、受到张力。双曲抛物面结合了两种方式的优点。凹下去的U型部分处于拉伸状态,而凸起来的拱顶部分则是压缩,高斯绝妙定理则保证了任何一个地方的受力都会传递到四周——因为这是一个高斯曲率非零的曲面。只要你试图改变它的形状,就必须得连带压缩或者拉伸一整片区域才能让结果遵从高斯的律令;像纸张那样只弯曲一条线而不影响其他部分是不可能的。通过这样的双重弯曲,这一形状实现了张力和压力之间的精妙平衡,让它以很小的厚度就能实现惊人的强度。
图片来源:Ciudad de las Artes y las Ciencias / Flickr
所以为什么薯片形状强度如此之高?这和它平衡张力与压力的方式有关。一切建筑都要支撑重量,最终将这些重量传递到地面上。这一传递可以靠两种不同方式完成:其一是压缩,拱顶就是纯靠压力而实现的例子;另一个就是拉伸,把一根锁链拎起来,它的每一环就都处于拉伸状态、受到张力。双曲抛物面结合了两种方式的优点。凹下去的U型部分处于拉伸状态,而凸起来的拱顶部分则是压缩,高斯绝妙定理则保证了任何一个地方的受力都会传递到四周——因为这是一个高斯曲率非零的曲面。只要你试图改变它的形状,就必须得连带压缩或者拉伸一整片区域才能让结果遵从高斯的律令;像纸张那样只弯曲一条线而不影响其他部分是不可能的。通过这样的双重弯曲,这一形状实现了张力和压力之间的精妙平衡,让它以很小的厚度就能实现惊人的强度。
通过弯曲来产生强度,这个想法塑造了我们所见的当代世界,而它的根源却来自万古不变的几何学。所以下一次你抓起一块披萨的时候,记得朝周围看看,欣赏一下这个简单的披萨小把戏背后的庞大遗产吧。(编辑:Calo)
高斯绝妙定理指出,这片披萨必须有至少一个方向永远保持平整——不管你怎么弯,它一定会留下一点“平”的痕迹。
相反,鸡蛋壳两个方向上都是弯的。这是它的关键。用数学语言表达,那就是这些双重弯曲的曲面拥有非零的高斯曲率。像我们先前遇到的橘子皮一样,这意味着它们不可能被压平,除非有撕裂或者拉伸——有高斯绝妙定理保证这一点。要打破一个鸡蛋,你必须首先弄出一个坑。等到鸡蛋失去了弯曲,也就失去了强度
数学
你拿披萨的方式,很可能是错的
高斯 曲面 曲率 平面 几何 几何学 空间 建筑 波形 建材 弯曲 波纹 强度 张力 拉力 双曲 抛物 受力
Aatish Bhatia 发表于 2014-10-17 17:30

(Ent/编译)我们都遇到过这种情况。你抓起一块披萨,正要一口吞掉的时候,披萨一下子软了,从你的指尖处耷拉了下来。披萨饼本身的结构强度不够高,无法支持整片的重量。也许下次应该少加点儿料?不用,无需绝望。
如果是是个吃披萨多年的老手,那你应该知道怎么对付这样的场景:只需把披萨弯成U形即可。(手头没有披萨?拿一张纸试验一下就好。)
 一张纸拿在手里就会耷下去,但弯曲握就能让它笔直。为什么呢?图片来源:Aatish Bhatia
一张纸拿在手里就会耷下去,但弯曲握就能让它笔直。为什么呢?图片来源:Aatish Bhatia拿一张纸,卷成圆柱形纸筒。你可能觉得显而易见,纸本来是平的,卷成筒就弯了,对吧?可是高斯不这么想。他想给纸的弯曲程度(“曲率”)下一个定义,让它不因你人工施加的弯曲而改变。
 图片来源:Aatish Bhatia
图片来源:Aatish Bhatia高斯的天才在于,他想到把所有这些路线都纳入曲率定义里面。办法是这样的:从任何一点出发,找到这只蚂蚁能选择的最极端的两条路线——也就是最凹的和最凸的两条线。然后把它们的曲率乘起来。凸的路线曲率是正的,凹的路线曲率是负的,直的路线曲率是0。你得到的数字,就是那个点上的高斯曲率。
 图片来源:Aatish Bhatia
图片来源:Aatish Bhatia相反,如果蚂蚁活在一个球上,那么它就无法找到平坦的路线,每一条道路都会有一定程度的向外凸出,所以高斯曲率一定是个正的数。所以,球是弯的,而筒是平的。你可以把一张纸卷成一个筒,却永远不能卷成一个球。
 图片来源:Aatish Bhatia
图片来源:Aatish Bhatia但这个定理还有一个绝妙的结果:你可以随意弯曲一个曲面,只要你不拉长、压缩或者撕裂它,高斯曲率一定不会变。因为单纯弯曲不改变其上的距离,所以不管怎么弯,上面的蚂蚁总会计算出同样的高斯曲率。
听起来可能有点儿抽象,但是这推论有十分紧贴现实的结果。把一个橘子切成两半,吃掉里面的东西,然后把剩下半个橘子皮放在地上,踩吧。皮永远不可能被踩扁成一个完整的圆。相反,它一定会裂开。这是因为球面和平面拥有不同的高斯曲率,所以不扭曲、不撕裂,是不可能把球面压平的。有没有试过给人寄篮球当礼物?包装纸会遇到完全一样的问题。不管你怎么弯曲一张纸,它总会留下一点点“平”的痕迹,所以最后只能得到皱皱巴巴一团糟。
 桔子皮不可能压成完整圆——因为球面和平面高斯曲率不同(而且桔子皮也没有什么延展性)。图片来源:Aatish Bhatia
桔子皮不可能压成完整圆——因为球面和平面高斯曲率不同(而且桔子皮也没有什么延展性)。图片来源:Aatish Bhatia 每个红色圆圈的实际面积是相等的,但在地图上看起来就有很大的差异。图片来源:Stefan Kühn (左), Eric Gaba (右) / Wikimedia
每个红色圆圈的实际面积是相等的,但在地图上看起来就有很大的差异。图片来源:Stefan Kühn (左), Eric Gaba (右) / Wikimedia 没想到几何学也能这么美味吧。图片来源:Aatish Bhatia
没想到几何学也能这么美味吧。图片来源:Aatish Bhatia 弯曲的草叶。图片来源:Dudley Carr / Flickr
弯曲的草叶。图片来源:Dudley Carr / Flickr 西班牙扎祖拉体育场。图片来源:Ximo Michavila
西班牙扎祖拉体育场。图片来源:Ximo Michavila 纸板箱里隐藏的秘密。图片来源:Craig Sunter / Flickr
纸板箱里隐藏的秘密。图片来源:Craig Sunter / Flickr 很多人小时候玩过的把戏:把一张纸折叠几次就能承载很大的重量,但它背后的数学可能你就想不到了。图片来源:Aatish Bhatia
很多人小时候玩过的把戏:把一张纸折叠几次就能承载很大的重量,但它背后的数学可能你就想不到了。图片来源:Aatish Bhatia今天,我们就算看到这些波浪形金属板也几乎不会多想什么。但当它们诞生时,许多人把波形建材看成是奇迹材料。1829年,亨利·帕尔默(Henry Palmer)获得了波形建材的专利,他是一个英国工程师,负责建造伦敦码头。帕尔默建起了世界上第一个波形钢结构建筑——伦敦码头的松油棚屋。虽然它今天看来可能没什么了不起,但是听听当时的一家建筑学杂志是怎么描述它的吧:
不久前路过伦敦码头时,我们十分满意地发现,帕尔默先生新发明的屋顶已经得到了实际应用。……任何一个目光敏锐的人,路过的时候都不可能不被它的优雅和简洁所打动(虽然它只是个棚屋);而只要稍加思索,他们就会相信这一建筑的效率之高、经济之节约。我们认为,这是自亚当诞生以来,人类之手所建造的最轻又最结实(以其重量而言)的屋顶。若我们仔细观察(我们为了这一目的而爬过了各式各样的粘稠松油罐),会发现这一屋顶的总厚度绝对没有超过十分之一英寸!
这年头的建筑学杂志真是大不如前了啊。虽然波形建材和易拉罐的强度可以很高,但有个办法让这些材料变得更强。想自己找到这个办法?去冰箱拿个鸡蛋出来。放在掌心,整只手握住鸡蛋,挤吧。(尝试这个的时候记得别戴戒指。)你会为它的强度而惊讶的。我就没法把鸡蛋握坏,哪怕用尽全力也没戏。(真的,谁试谁知道。)
 请务必在家中尝试一下——好吧,为了安全,别在电脑前尝试。图片来源:Aatish Bhatia
请务必在家中尝试一下——好吧,为了安全,别在电脑前尝试。图片来源:Aatish Bhatia相反,鸡蛋壳两个方向上都是弯的。这是它的关键。用数学语言表达,那就是这些双重弯曲的曲面拥有非零的高斯曲率。像我们先前遇到的橘子皮一样,这意味着它们不可能被压平,除非有撕裂或者拉伸——有高斯绝妙定理保证这一点。要打破一个鸡蛋,你必须首先弄出一个坑。等到鸡蛋失去了弯曲,也就失去了强度。
 图片来源:Owen Cliffe / Wikimedia
图片来源:Owen Cliffe / Wikimedia另一种得益于弯曲的形状是品客“薯片”,照数学家的说法,这是个双曲抛物面(hyperbolic paraboloid,舌头打结了没?)。
 图片来源:Aatish Bhatia
图片来源:Aatish Bhatia西班牙-墨西哥建筑师菲利克斯·坎德拉(Félix Candela)很懂薯片形状的力量。坎德拉是托罗亚的学生,他的建筑将双曲抛物面带到了新的高度(字面意思)。当你听到“混凝土”这个词的时候,恐怕只会想到无聊透顶的方块建筑,但坎德拉却利用双曲抛物面盖起了巨大的建筑,使用的混凝土薄到不可思议。身为这一材料的真正大师,他既是极富创新的建筑者,也是结构艺术家。
 图片来源:Ciudad de las Artes y las Ciencias / Flickr
图片来源:Ciudad de las Artes y las Ciencias / Flickr通过弯曲来产生强度,这个想法塑造了我们所见的当代世界,而它的根源却来自万古不变的几何学。所以下一次你抓起一块披萨的时候,记得朝周围看看,欣赏一下这个简单的披萨小把戏背后的庞大遗产吧。(编辑:Calo)
参考资料
- Reid, Esmond. Understanding buildings: a multidisciplinary approach. MIT Press, 1984.
- Mornement, Adam, and Simon Holloway. Corrugated iron: building on the frontier. WW Norton & Company, 2007.
- Garlock, Maria E. Moreyra, David P. Billington, and Noah Burger. Félix Candela: engineer, builder, structural artist. Princeton University Art Museum, 2008.
编译来源
wired.com, How a 19th Century Math Genius Taught Us the Best Way to Hold a Pizza Slice- 热谱 正则系综 幺正性 信息
- 序参量 φ(r)不是原子尺度的物理量,而是宏观小微观大的物理量
- 取热力学极限时,由于体积趋于无穷大,因此,实际处理的是一开放系统。在这一开放系统中,取有限大小的体积...
- 有限系统的配分函数是解析函数,不存在奇点,因而 不会有相变发生。只有在热力学极限下,配分函数才会出现...
- 热力学极限:粒子数和体积都是无穷大,但其比值保持一定。此时,系统基本处于平衡态,对其偏离仅是微小的涨...
- brain 塌缩理论与量子力学的其他要素完全不同,是一种非幺正过程,或者说损失信息的过程
- 二维球面没有边界,但是你的视野却有个范围的,于是存在一个界限。我们的宇宙有这样一个界限,由于光速有限...
- 开放系统: 摩擦力(非保守力), 沒有位能,力學能通常會損耗,推力.摩擦力.阻力都是 热只能从高温传...
- 束缚在原子核内的能量向空间传播这一过程可以被认为是无序程度增大
- “U” ①分子运动 ... 原子间的位能, 如:质子与质子间的作用,化学键能等, 不包括系统整体运动...
- 內能 系統的一個態函數 U 是系统自身的性质,其绝对值难以确定 include 原子核内的能量 化...
- 热力学第一定律 系统从状态A 变化到状态B,可以采用做功和传热 不管经过什么过程,只要始末状态确...
- 热力学能,过去长期叫内能,符号U,是系统内各种形式能量的总和,例如系统中分子的动能(分子运动包括平动...
- 保守力:作功可以轉換成位能儲存,非保守力:沒有位能的概念,自然也談不上位能儲存, 3.F是某個(位能...
- 超声医学基础
- 在气体和液体中传播的声波是纵波;而在固体中传播的声波既有纵波,又有横波,且两种波的波速不同,纵波的速...
- 水分子的振動並非單純的與波前進的方向垂直或平行,因此並不適合討論其為橫波或縱波
- 電磁波包含二個橫波
- the fock space of quantum field theory include sta...
- The Hilbert space of all realistic systems is infi...
- 开普勒微分方程 迭代求解, 二体运动的位置和速度, 双曲线轨道
- AdS 空間是一個有重力位能井(gravitational potentialwell)的大箱子,大...
- M 理論 strong/weak duality 兩個理論能譜中的基本粒子(elementary p...
- 量子重力的本質基本上得遵守面積律, 也就是應當是全像式的, (holographic),這就是所謂的...
- 弦論放棄了時空的點集特性, 避開了無法重整化自能, 弦論在低能量的狀況下可以逼近廣義相對論
- 非平衡量子場論 宇宙暴脹後,宇宙的能量如何從非穩定態的位能能量, 轉換成充滿相對論性粒子,此為輻射 ...
- 極高溫的狀態下開始. 膨脹,至今天我們所. 看到的樣子; 在低温极限(T 《 8) 日动得到通常的量...
- 引力波想象成地震发生后向外传播的地震波,只不过时空中这些“震荡”的源头都是一些高能天文现象, 黑洞与...
- 伽利略变换下的“普适的新经典热力学”
- 平动变换是伽利略变换,转动变换叫欧拉变换, 能等于质量乘以重力加速度再乘以高度,没有时空哪来的加速度...
- Mach提出“物体并没有绝对加速度,只有相对遥远星系的加速度,Mach思想的可取之处是在于不能抽象脱...
- ◦凸集可开可闭可半开半闭。函数曲线的上面部分是开的, 二次连续可微
- 晶体中简谐振动的3NS 个格波的总能量,通过引入简正坐标消去交叉项后很容易的证明了晶格振动能量可以看...
- 德拜模型正确地预言了低温时固体的热容,与T3成正比。就像爱因斯坦模型一样,它在高温时也与杜隆-珀蒂定...
- 得拜模型 声子对固体的比热(热容)的贡献。它把原子晶格(热)的振动视为盒中的声子 , 把原子晶格(...
- 在等位势面上重力平移不作功
- 單擺只受重力和張力作用,張力不作功,所以力學能守恆; 当力始终与质点位移垂直时,该力不作功
- 刚体的运动可看作是质心的平动; 系统体积不变的情况下,外界对系统不作功, 对于具有三个平动自由度的粒...
- 资本市场相对来说实现了金融体系的熵的最大化
- 平动 平移变换 同一质点相对于两个相对做平动的参考系的速度之间的这一关系叫做枷利略速度变换。
- 平动由力产生,而在转动中,力矩的概念占据着关键的主导地位, 力矩做功是在转动中力做功的一种特殊形式,...
- 力矩无法和平动做功相关,但能和转动做功相关, 把角度看成广义坐标,那么力矩就是对应的广义力。(再举个...
- T是温度,在热力学中反映粒子所具有的能量,E是势垒高度,可以理解为一堵墙。整个指数项反映的是具有一定...
- white 数学期望 一阶原点矩(表示分布重心)、方差是二阶中心距(表示离散程度)、偏态是三阶中心...
- 引力系统复杂的地方在于,它是一个极端普适的力,他跟所有的东西都有 coupling,所有形式的能量,...
- 把测量者放在了一个特殊的位置上了: Hilbert 空间的矢量来代指状态,这个抽象的状态本身没法诠释...
- 经典的电场和磁场都是光子的相干态(就是那所谓最小不确定态),相干态也是最高权态,最小不确定态相干态只...
- 正负电子对撞, 一种正负粒子碰撞的机制, 提供从真空紫外光到硬X光的很大光谱范围的同步辐射光; 孤立...
- baba94 如果辐射源中质点远离热动平衡分布,则其辐射称为非热辐射; 如果辐射源(等离子体、中性...
- 热学讲义 固体中的每个分子的振动相互耦合,将振动在晶体中传播,形成格波
- baba94 热波理论 在固体中, 由于电子与电子, 电子与声子, 声子与声子间相互作用, 造成近邻...
- 4f 電子為局域性很強的電子, 玻璃态到液态的整个温度范围内的分子/集团的移动机理
- 把无序系统模型化为一个晶格系统,系统的每一个元胞具有一个局域约化温度,局域约化温度的随机部分符合高斯...
- 温度和电流密度会对对称性有影响。当温度升高,我们会发现对称性恢复了,当增加电流密度,我们也会发现对称...
- atom 不同环境下原子的尺度,它们的尺度是由测量分子或固体中原子间的距离之后再进行适当的分配而决定...
- 原子的质量为10-22—10-24g,比电子的质量大3-5 个数量级,电子对原子质量的贡献很小.而....
- 轨道半径越小,动能越大,所以D正确; (玻尔半径) 势能与动能数量级比较: E v /E; 原子的质...
- xiaoniudun.xatyz.com 假定原子核是一个立方体,有n×n×n个核子,每个核子被其他...
- 水银(原子序号为80)来说,这种效应就很重要了,它的电子的速度接近光速的58%,它的运动质量是静止质...
- 水银(原子序号为80)来说,这种效应就很重要了,它的电子的速度接近光速的58%,它的运动质量是静止质...
- 波尔模型是正确的,实验值和理论值的偏差在于原来的理论假定氢核禁止,但是实际电子绕核运动时核不是固定不...
- 質子是在大爆炸後約十萬分之一秒產生的,而電子約是在四秒鐘後形成; 氧是一個比較難計算準確的原子。
- 相对论效应源自重原子内层电子的运动速度。当内层s 电子的运动速度达到堪与光速相比的程度时, 根据Ei...
- 物体的运动速度突破某个速度范围的时候,他们的质量会改变,而且跟他们的速度有关。汞原子中最外层电子速度...
- string theory Particles in a string theory are lik...
- 不存在作简谐振动的孤立质点, 考虑引力辐射时必须考虑整个体系; 黎曼, 利用測量在局部畫出測地線, ...
- 混沌振动。庞卡莱在上个世纪末已经认识到不可积系统存在复杂的运动形式,运动对初始条件具有**依赖性,现...
- 薛定谔方程Ψ=ψ。cos[2π﹙Et-px﹚/h]不是从任何物理机制中得出来的,它纯粹是机械波方程y...
- 簡諧運動超過10度就不能視為簡諧運動
- 单摆和复摆在较小角度情况下,作周期性简谐振动,具有等时性
- white 简谐振动具有等时性,即一个做简谐振动的质点运动周期和振幅以及相位无关, 运动轨道与质量没...
- 非线性作用具有非独立相干性:“一个微小的因素能导致用它的幅值无法衡量的效果 , 周期3意味着混沌; ...
- 从圆映射到区间映射,从二维映射到一维映射,其认为混沌意味着周期三,混沌就是一个折叠,而其的符号系统就...
- Bertrand 定理:只有两种类型的有心力场,其中一切有界运动的轨道是封闭的,这两种场的势能与1 ...
- white gauge 混沌 映射混沌 周期三 导致混沌 一个椭圆是封闭的,这样的对称性背后,包含...
- white 把一个曲线与一个代数方程等同起来,这样的想法把代数和几何结合起来,这样的结合是思想的奇葩...
- 每一个解都对应着一个可能存在的宇宙: 爱因斯坦引力场方程包含了10 个变量和10 个相互独立的子方程...
- 當星體、四大尖軸(例如上升點ASC、天頂MC等)、阿拉伯點(例如幸運點等)及星盤中的其他敏感點之間形...
- 狭义相对论和量子理论一元化表述; 双曲复空间RH同构于四维Minkowski时空,而其上的双曲相位变...
- 广义相对论和双曲方程
- isis targeting RNA (“RNA Therapeutics”) resulting ...
- Green 定理與應用 積分, 僅需求得函數 f 之原函數 F, 一個函數之微分的積分值等於該函數...
- 流形上的曲线和函数在局部上有很好的性质,比如说线性性质; 切向量與法向量形式的 Green 定理,而...
- 測地線確代表兩點之間的最短距離。一旦走遠了就不一定是最短的, 切向量微分以後當然指向經圓的圓心,和...
- white 电子在晶体周期势场中运动 把自由电子气等效为在温度T=0K,V =L3 的立方体 内运...
- white 原子只能较长久地停留在一些稳定状态(简称定态),原子在这些状态时,不发出或吸收能量;各定...
- “等效原理的动力学性质”, 根据功能原理, 态缺失电子的近满带电子电流,等效于一个正电荷产生的电流,...
- 球面上的測地線 緯圓的周長會因緯度而變; 當 是九十度的時候, 它代表赤道, 动能不转化位能的运动...
- 測地線(那根一定要通過圓心的線),所有地球上任何圓的中心和地球圓中心重合的,都是地球的測地線
white01 zeta01 gammacomplex01 diffgeorm01 manifold01 trading01 一张纸(2次元),纸上有A B两点,现在折 要在11次元动一下的,你动这一下被干扰可就是11次元坐标变动,更是死得惨 ; 固有时是观测者手中钟表的读数,是实际测量的时间,坐标时是四维时空坐标中的一个坐标分量(坐标时没有实际物理意义)
"角動量伪矢量")【位移】【时空曲率】
为从初位置到末位置的有向线段,其大小与路径无关,方向由起点指向终点。
11次元的位移依旧是位移! 不过是x y z 变多了
高维度位移 大家可以想向一张纸(2次元),纸上有A B两点,现在折(可以不真折 弯个弧一样)几(一)下,使A B重合。很轻松吧,具体怎么折有多种方法。折好之后再从A到B就不用在纸上走好远了。
同理,3次元的瞬间移动只要扭曲3维空间,使起点和终点重合,之后一步就可以跨过好远。不过扭曲空间的程度(时空曲率)是矢量。你敢让一方碰到这个弯折,就等死吧。而且你还是要在11次元动一下的,你动这一下被干扰可就是11次元坐标变动,更是死得惨


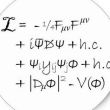

引力场方程
对应原理
11次元的位移依旧是位移! 不过是x y z 变多了
高维度位移 大家可以想向一张纸(2次元),纸上有A B两点,现在折(可以不真折 弯个弧一样)几(一)下,使A B重合。很轻松吧,具体怎么折有多种方法。折好之后再从A到B就不用在纸上走好远了。
同理,3次元的瞬间移动只要扭曲3维空间,使起点和终点重合,之后一步就可以跨过好远。不过扭曲空间的程度(时空曲率)是矢量。你敢让一方碰到这个弯折,就等死吧。而且你还是要在11次元动一下的,你动这一下被干扰可就是11次元坐标变动,更是死得惨
爱lixiufei123: 众所周知,狭义相对论中定义的“固有时间“Δτ 在洛伦兹变换中保持不变,属于标量。静坐标系中“固有时间“Δτ 表示这个物理过程发生的时间量;动坐标系中Δt表示物理过程发生的时间量。那么,“固有时间“Δτ在动坐标系中有什么物理意义呢?
还有2条回复,点击查看
固有时是观测者手中钟表的读数,是实际测量的时间,坐标时是四维时空坐标中的一个坐标分量(坐标时没有实际物理意义)
以上是广义相对论对有关“时间”问题的回答,我奉劝楼主,最好不要拿狭义相对论套广义相对论..........
以上是广义相对论对有关“时间”问题的回答,我奉劝楼主,最好不要拿狭义相对论套广义相对论..........
引力场方程
2015年2月24日 19:09
.爱因斯坦场方程:
 刻上真空场方程式的纪念硬币
R_uv-1/2*R*g_uv=κ*T_uv
刻上真空场方程式的纪念硬币
R_uv-1/2*R*g_uv=κ*T_uv
 刻上真空场方程式的纪念硬币
刻上真空场方程式的纪念硬币
(Rμν-(1/2)gμνR=8GπTμν/(c*c*c*c) -gμν)
说明:g_uv为度规,κ为系数,可由低速的牛顿理论来确定。"_"后字母为下标,"^"后字母为上标。
意义:空间物质的能量-动量(T_uv)分布=空间的弯曲状况(R_uv)
解的形式是:ds^2=Adt^2+Bdr^2+Cdθ^2+Ddφ^2
式中A,B,C,D为度规g_uv分量。
考虑能量-动量张量T_uv的解比较复杂。最简单的就是让T_uv等于0,对于真空静止球对称外部的情况,则有施瓦西外解。如果是该球体内部的情况,或者是考虑球体轴对称的旋转,就稍微复杂一点。还有更复杂的星云内部或外部的情况,星云内部的星球还要运动、转动等。这些因素都要影响到星云内部的曲面空间。
2.含宇宙常数项的场方程:
R_uv-1/2*R*g_uv+Λ*g_uv=κ*T_uv
此处的Λ是宇宙常数,其物理意义是宇宙真空场。Λ*g_uv为宇宙项。
如果从数学上理解的话,则上面的场方程也可解出下面的形式:
ds^2=Adt^2+Bdr^2+Cdθ^2+Ddφ^2![[1] [1]](http://img.t.sinajs.cn/t4/appstyle/expression/ext/normal/82/one_org.gif)
![[1] [1]](http://img.t.sinajs.cn/t4/appstyle/expression/ext/normal/82/one_org.gif)
式中A,B,C,D为度规g_uv分量。
这里的ds就是表达空间弯曲程度的一小段距离。同时因为4维空间与时间有关,ds随时间也会变化。这时,如果没有宇宙项,ds随时间是增大的,宇宙就是膨胀的。如果加了宇宙项,选取适当的Λ值,ds不随时间变化,宇宙就是稳定的。
如果从物理意义上理解的话,把宇宙项移到式右边,则是:
R_uv-1/2*R*g_uv=κ*T_uv-Λ*g_uv
Λ项为负值,起到了斥力的作用,即宇宙真空场与普通物质场之间存在着斥力。宇宙项和通常物质场的引力作用起到了平衡的作用,所以可得到稳定的宇宙解。
2性质编辑
非线性
爱因斯坦场方程的非线性特质使得广义相对论与其他物理学理论迥异。举例来说,电磁学的麦克斯韦方程组跟电场、磁场以及电荷、电流的分布是呈线性关系(亦即两个解的线性叠加仍然是一个解)。另个例子是量子力学中的薛定谔方程,对于概率波函数也是线性的。![[1] [1]](http://img.t.sinajs.cn/t4/appstyle/expression/ext/normal/82/one_org.gif)
![[1] [1]](http://img.t.sinajs.cn/t4/appstyle/expression/ext/normal/82/one_org.gif)
对应原理![[抱抱] [抱抱]](http://img.t.sinajs.cn/t4/appstyle/expression/ext/normal/27/bba_org.gif)
透过弱场近似以及慢速近似,可以从爱因斯坦场方程退化为牛顿重力定律。事实上,场方程中的比例常数是经过这两个近似,以跟牛顿重力理论做连结后所得出。
牛顿重力理论 is like 电场、磁场以及电荷、电流的分布是呈线性关系, 線性疊加
批踢踢實業坊 › 看板 Physics 關於我們 聯絡資訊
相对论与黎曼几何-7-黎曼几何 精选
精选

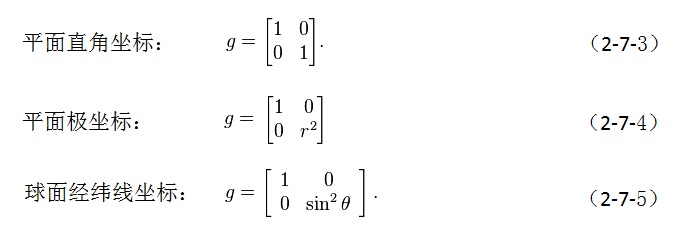
發信人tmg@kkcity.com.tw (大斜妖刀雪崩土石流),
看板Physics
標 題Re: 請問分離變數法的物理意義....????
發信站KKCITY (Fri Jun 20 23:34:07 2003)
轉信站Ptt!news.ntu!bbs.ee.ntu!news.ee.ntu!news.kkcity.com.tw!KKCITY
※ 引述《couch》之銘言: 會使用分離變數法,通常是因為以下的特性: 線性方程的解,作線性疊加之後,仍然滿足原方程 因為這個特點,所以,我們對於解線性(偏)微分方程,得到一個重要的提示: 如果我們可以找到足夠多的解當基底 所有滿足這個方程的解,都可以透過線性疊加的方式合成 因此,我們就可以使用線性代數的技巧,使計算更為方便 這裡有三個主要的考量點: 1. 如何確定找到的解夠多,足夠當成基底來用 2. 找基底的方法是否夠簡單。 如果還要花一大堆力氣找基底,抵消掉使用線性代數變成更加方便的好處 那就失去做這件事情的意義了 3. 我所找到的基底是否適用於我想解的問題。 即使是線性疊加,但許多時候我還有其它的條件限制,例如邊界的長像 使得某些基底並不適用於我想解的問題 ---------- 分離變數法最大的精神是,想辦法把偏微分方程變成常微分方程 這個過程,使得解偏微分方程的難度,降低好幾個數量級 因此滿足條件 (2) 而最大的問題是,"我會不會漏掉某些解沒找到"? 換句話說,到底條件 (1) 滿不滿足 這件事情,很幸運地,在數學上可証明 使用分離變數法找到解,足夠多到可以當基底使用 所以現在問題就只剩下條件 (3) 了...... ---------- 這時,一個很重要的觀念必須引入:對稱 我們發現,當我們所解的問題滿足某種對稱時 解的長像似乎也會滿足某種對稱性 這讓我們又有另一項提示:座標系的選取 當我們所解的問題 其邊界長像是方形對稱時,二話不說就用直角坐標系 而長像是柱狀對稱時,就使用圓柱坐標系 而長像是球狀對稱時,就使用球坐標系 總之,座標系的選取,要儘量滿足所解問題的對稱條件 那如果沒有滿足對稱條件,是不是不能解? 不是,還是可以解,只不過,當你在縫合邊界條件時 因為坐標系與邊界不對稱,你一定會一邊縫合一邊訐譙 !@#$%^&* 當然當你花了一堆力氣縫合完成時,你也得到了正確解答 ---------- 其實,當我們使用分離變數法時, 我們發現,在許多情況,我們都在解以下的問題: A(x) f(x) = λ f(x) A(x) 代表一個線性運算子,例如 d/dx, 或 (d^2/dx^2 + x^2) ... 等 λ是一個常數 眼尖的人一看,就明白這是個典型的 eigenvalue problem 想辦法找到這個方程的 eigen function 就好了 不過在許多時候,eigenvalue 與 eigen function 並不是那麼容易找 所以,通常我們會使用一些技巧,作變數變換成以下的形式 B f(y) = λ f(y) B也是一個線性運算子,不過與A不同的是,B是常線性運算子,與 y 無關 簡化到這個地步,我們可以使用葵花寶典了 Laplace transform 或 Fourier transform 將這個問題變成代數方程式,問題難度再降低幾個數量級 ---------- 當問題變簡單,你可以爽爽地算 你會發現,最後一步通常都是縫合邊界條件 不過縫合時,又會碰到一顆小小的石頭 就是,各個可能解的係數要怎麼挑,才會滿足邊界條件 這一點,就想辦法拿出你家的剪刀菜刀剃頭刀 使用各種學過的工具,如 Laplace Fourier z conformal.... 得到你要想的係數 這時就功德圓滿大功告成了 ---------- 咦?會不會你只找到一種可能解 會不會存在其它解,同時滿足此偏微分方程,與所給定的邊界條件 嗯,這是所謂解的唯一性問題 這個問題,我們經由數學証明,會得到一些條件 以我們常遇到的線性偏微分方程而言,大部分都是二次偏微分方程 而二次方程分成三大類:橢圓方程(位能),雙曲方程(波動),拋物方程(熱傳導) 這三大類方程的唯一性,則由邊界條件是否滿足某些特性而決定 很幸運地,在大部分我們所處理的狀況,解的唯一性是成立的 ※ 引述《couch》之銘言: > ※ 引述《ccos.bbs@bbs.ntu.edu.tw (vee vee vee vee)》之銘言: > > 第一次聽到這種說法 感覺很新鮮 小時候基本上是管他三七二十一算出答案 > > 就不管了 現在年紀大了才知道要多想 不知道您上述的講法是從哪本書看來 > > 的 想找來翻翻 > > by Cheng Cosine > > Jun/07/2k3 Ut > mmm.... > 這些是老師上課提到的觀念 > 我不知道書找不找的到 > 但講一些我聽到的東西好了 > 像在解擴散的Fick's second law時 > short time會用Green's function的方法解 > 解出所謂的thin film solution(是個Gaussian function) > 然後再利用boundary condition來決定要怎麼把這些Gaussian functin加起來 > long time時則用分離變變數(跟前面提到的decouple有關) > 分完了你愛用哪種transform或級數展開把解算出來就隨便你囉 > 這兩種方法的不同除了以上所說的 > 還有一個就是級數要收斂的問題 > 倒過來用應該也是可以解 > 只是寫出來的解會寫到手軟還不一定收斂得下來 > 量子力學的話會瞰的解釋(以氫原子來說) > 單從分離變數方法來看 > 可能就只能說是數學上解pde的手法 > 但是因為氫原子是central force problem > radial的部分的operator(這我沒聽過有名字) > 和L^2 , Lz三者是commute > 所以三者各自的eigentfunction可以分開來解 > 而且可以用乘法湊起來 > 從operator的觀點來看就可以去interpret分離變數法 > 但我覺得以上只是物理各領域中的不同看法 > 重點應該是用分離變數法解出來的解可以用來展開任何可能的解 > 所以管他解出來對不對 > 反正對的答案最後一定可以湊出來就好啦相对论与黎曼几何-7-黎曼几何
7. 黎曼几何
在介绍“内蕴几何”一节中说过,高斯以他的“绝妙定理”建立了曲面内在的微分几何。之后,是高斯的得意门生黎曼,将曲面的概念扩展到流形(Manifolds),将内蕴几何扩展到n维的一般情形,建立了黎曼几何。
和高斯一样,黎曼(1826-1866)也是德国数学家,同样出生在贫困的普通家庭。黎曼比高斯刚好小五十岁,于1826年生于德国的一个小村庄,有趣的是,按时间算起来,高斯那时候正好在这个地区进行土地测量。时间的巧合,给人一种异想天开神话式的联想:上帝是否就在那时候,将非欧几何-黎曼几何的思想种子,植根到了那片被丈量的土地上。
遗憾的是,黎曼只活了39岁,不过,他短暂的一生,却对数学做出了杰出的贡献。他小时候家境贫困,但父亲是教堂的牧师,很重视儿子的教育,也注意到黎曼在数学上的杰出能力。因此,父亲没有为了尽早改善家庭的经济状况而阻止黎曼往数学的方向上发展,这才有了现代数学上著名的黎曼面、黎曼几何、黎曼猜想、……等等。
黎曼19岁进入哥廷根大学读书时,高斯将近70,已经是那儿鼎鼎有名的教授,正是在听了高斯的几次数学讲座之后,黎曼才下决心改修数学。
1847年,黎曼转入柏林大学学习,也许是冥冥中某种力量的召唤,两年后他又回到哥廷根大学攻读博士学位,成为高斯晚年的学生。博士毕业后,黎曼为了申请哥廷根大学的一个“无薪”教职,需要作一个难度颇高的就职演说。为了确定论文的选题,他向高斯提交了3个题目,以便让高斯在其中选定一个。没想到高斯选中了黎曼当时并没有多少准备的几何基础题目。更没想到的是,正是这篇黎曼花了不到两个月时间准备出来的演讲论文《论作为几何基础的假设》(原文见【1】,英文翻译版见【2】),提出了一大堆陌生概念,开创了一种崭新的几何体系,令哥廷根的数学同行们大吃一惊。
某些传言可能并不过分,据说当时在黎曼就职演讲的听众中,唯有高斯听懂了黎曼在说些什么。
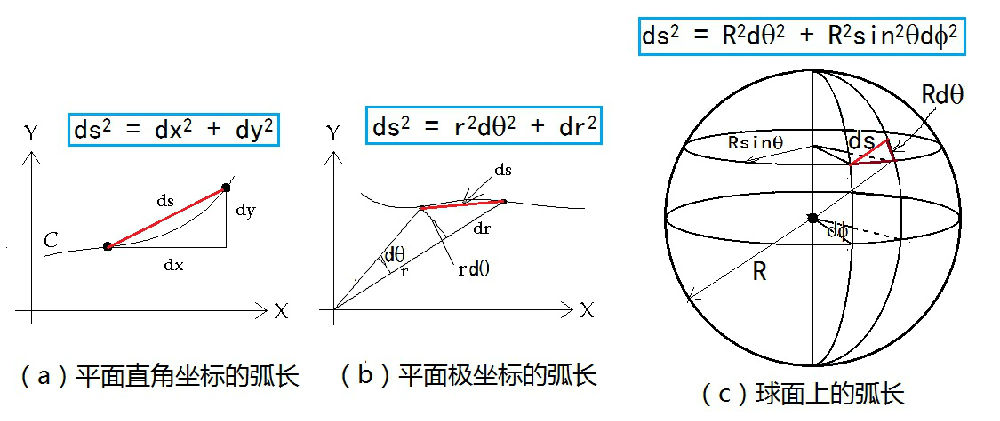
从前面“内蕴几何”一节中,我们已经知道:根据曲面的第一基本形式,也就是曲面上计算弧长的公式,可以建立起曲面的内蕴几何。三维空间中两个参数u和v所描述的曲面的第一形式可用下式表达:
ds2 = E du2 + 2F dudv+ G dv2 (2-7-1)

图2-7-1:平面(a、b)和球面(c)上的弧长(微分)表达式
公式(2-7-1)中的E、F、G是曲面第一基本形式的系数。黎曼在他的就职演说中,将二维曲面的概念扩展为“n维流形”,将E、F、G等系数扩展为定义在n维黎曼流形上每一点p的“黎曼度规”gij(p):

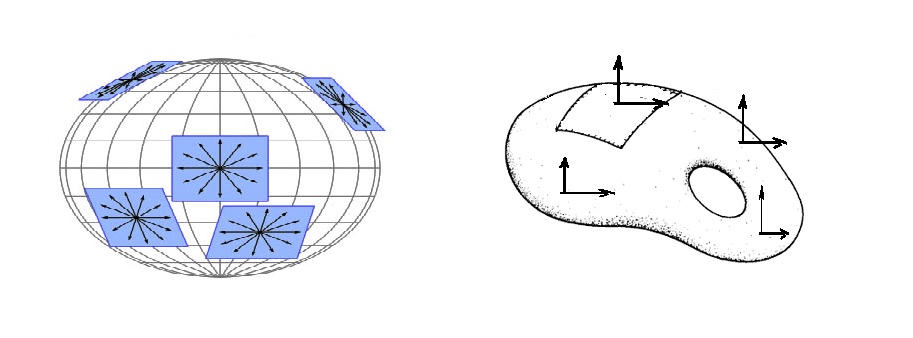
有了度规,就有了度量空间长度的某种方法,也就才能够测量和计算距离、角度、面积等等几何量,从而建立流形上的几何学。首先,我们可以从图2-7-1所示的平面和球面上的弧长微分计算公式,对黎曼度规gij得到一点直观印象。对图中的二维平面和二维球面,下指标i和j的取值从1到2,这时,可以将度规gij写成2×2的矩阵形式:
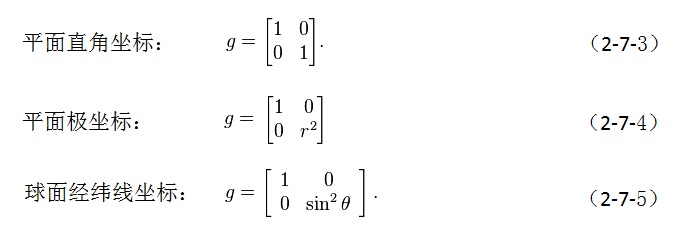
总结一下上面3种情况下度规的性质:a.平面直角坐标的度规是个简单的dij函数(i等于j时为1,否则为0),而且对整个平面所有的p点都是一样的;b.平面极坐标的度规对整个平面不是常数,随点p的r不同而不同;c.球面坐标上的度规也不是常数。由上面a和b的结论可知:同样是描述平面,但如果所选择的坐标系不同,度规也将不同。平面上的极坐标和直角坐标是可以互相转换的,因此,第二种情况b的极坐标度规可以经过坐标变换而变成a那种dij函数形式的度规。那么,现在就有了一个问题:第3种情况的球面度规是否也可以经过坐标变换而变成如a所示的那种d形式的度规呢?对此数学家们已经有了证明,答案是否定的。也就是说,在ds保持不变的情形下,无论你作何种坐标变换,都不可能将球面的度规变成a所示的d形式。由此表明,球面的内在弯曲性质无法通过坐标变换而消除,黎曼度规可以区分平面和球面或其它空间的内在弯曲状况。
一般来说,黎曼流形上每一点p的“黎曼度规”gij(p)随p点的不同而不同,这种以空间中的点为变量的物理量叫做“场”。
像黎曼度规gij(p)这种具有两个指标(i和j),并且在坐标变换下按一定规律变化的几何量叫做二阶张量。因此,gij(p)是黎曼流形上的2阶张量场。不难看出,对n维流形上的点p,gij(p)在给定的坐标系中有n2个分量,因而可以表示成一个n×n的矩阵。除了2阶张量场之外,黎曼流形上也能定义0阶张量(标量)场、1阶张量(矢量)场、3阶、4阶以及更高阶的张量场。
张量在物理及工程上有广泛的应用,尤其是大家所熟知的“矢量”的概念,连日常生活中也都比比皆是:速度、加速度、力、电流、水流、电场、磁场等等,这些既有方向,又有大小的物理量,都可以用矢量来表示。n维空间的矢量有n个分量,标量则只有1个分量,比如温度、湿度、密度、能量等,属于标量。
物理量表达的是某种物理实在,应该与人为选择的坐标系无关。因此,标量、矢量、张量等,都是独立于坐标系而存在的。只不过,为了测量和计算的方便,人们总是要选取一定的坐标系,这样一来,这些量在不同的坐标系之下,便有了不同的分量值。然而,无论坐标系如何选取,因为总是对应于同一个东西,总有些量是不会改变的。因此,在坐标系变换时,张量的坐标分量便必须遵循某种规则,才能保证这一点。就好比对于同一个人,不同的人对他可以有不同的称呼:“爸爸”、“儿子”、“爷爷”、“哥哥”、“弟弟”,都有可能。但是,这些称呼之间的变换应该会符合某些逻辑原则,才能保证它们指的是同一个人。
有时候,坐标系的选取可以简化计算,或者更清楚地表征空间的某种性质。前面所说的度规张量就是如此。如果一个黎曼流形上每一点的的度规张量都可以写成dij函数形式的话,黎曼将其称之为“平”流形。流形“平”或“不平”,定义在它上面的几何规律将完全不同。
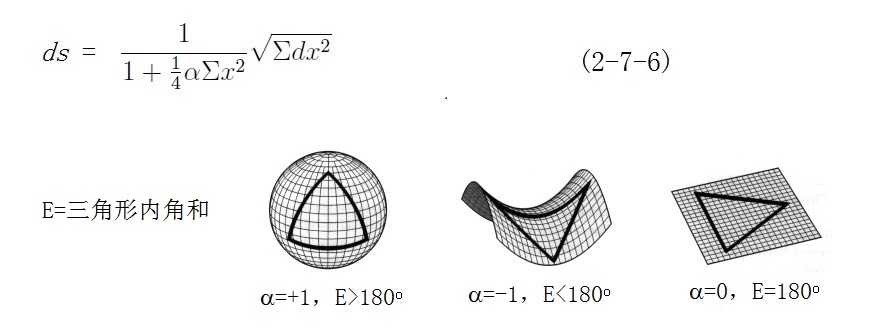
黎曼将二维曲面的球面几何、双曲几何(即罗巴切夫斯基几何)、和欧氏几何,统一在下述黎曼度规表达式中:

公式(2-7-6)中的a,是2维曲面的高斯曲率。当a=+1,度规所描述的是三角形内角和E大于180度的球面几何;当a=-1,所描述的是内角和E小于180o的双曲几何;当a=0,则对应于通常的欧几里德几何。黎曼引入度规的概念,将3种几何统一在一起,使得非欧几何焕发出蓬勃的生机。
如同我们看到的嵌入三维空间中的大多数二维曲面都不是可展的一样,大多数流形都不是“平”的。高斯定义了高斯曲率来描述平面和“不可展”曲面的差异,黎曼将曲率的概念扩展为“黎曼曲率张量”。那是n维流形每个点上的一个四阶张量,张量的分量个数随n的增大变成很大,并且表达式非常复杂。不过,由于对称性的原因,可以将独立的分量数目大大减少。
也可以用黎曼定义的“截面曲率”来描述流形的内在弯曲程度。为此需引进过流形上一点p的切空间的概念。在这儿需要强调的是,黎曼研究的是一般情况下的n维流形,通常n>=3,但我们人类的大脑想象不出,计算机也画不出来这些高维而又“不平坦”的流形是个什么样子,所以只好用嵌入3维空间的2维曲面的图像来表示这种“弯曲”流形,如图2-7-2所示。

图2-7-2:流形和过每一点的切空间
一个n维流形过点p的切空间是一个n维的欧氏空间。设Pp是这个欧氏切空间中的一个平面,截面曲率 K(Pp) 定义为以Pp作为切平面的n维流形过p点的那个2维截面的高斯曲率。在特别情况,如果n=2的话,即对2维流形而言,只有一个截面曲率,正好就是原来的高斯曲率。
上面的表述对n大于2的情况不好直观想象,对n等于2又稍微显得平凡。尽管如此,从图2-7-2中,我们仍然可以将2维曲面图像添加一些想象而延伸到一般的流形及其切空间,从而得到某种直观印像。
黎曼是把流形概念推广到高维的第一人。流形的名字来自他原来的德语术语Mannigfaltigkeit,英语翻译成manifold,是多层的意思。一般的流形,不但“不平”,而且其“不平”度还可以逐点不一样,流形的整体也可能有你意想不到的任何古怪形状。不过,黎曼流形仅仅指其中定义了黎曼度规的可微分流形。
形式上来看,黎曼是将高斯的2维曲面几何推广到了n维,但实际上黎曼所做工作的意义远不止于此。首先,高维流形中的曲率的概念要比2维曲率丰富得多。此外,因为黎曼度规是基于弧长微分ds的计算公式,所以黎曼几何完全不同于之前的欧几里德几何,或笛卡尔坐标几何那种对整个空间都适用的几何学,而是一种局部化的几何。这是黎曼在几何上迈出的革命性的一步。研究黎曼几何时,我们不需要整个空间,只需要其中局部的一小块就够了。在黎曼流形上的每一点,都可以定义一个切空间,从而再进一步建立起黎曼流形上的微分运算等,这些将在下一节中介绍。
参考资料:
【1】Ueberdie Gesetze der Vertheilung von Spannungselectricität in ponderabeln Körpern,wenn diese nicht als vollkommene Leiter oder Nichtleiter, sondern als demEnthalten von Spannungselectricität mit endlicher Kraft widerstrebendbetrachtet werden
(Amtlicher Bericht über die 31. Versammlung deutscher Naturforscher undAerzte zu Göttingen im September 1854)
【2】On theHypotheses which lie at the Bases of Geometry
(Bernhard Riemann, translated by William Kingdon Clifford, Nature, 8(1873), 14-17, 36-37)
No comments:
Post a Comment